浙江省宁波市鄞州区2023年初中学业水平模拟考试数学试题

试卷更新日期：2023-05-12 类型：中考模拟

进入出卷网下载

一、选择题(每小题4分，共40分.)

1. 在下列实数中，属于无理数的是（）

A、2023 B、- 2023 C、 $\sqrt{2023}$ D、 $\frac{1}{2023}$

查看试题解析
2. 下列计算正确的是（）

A、a³+a³=2a⁶ B、a³xa³=a⁶ C、a⁶÷a³=a² D、(3a)³ =9a³

查看试题解析
3. 2022年，鄞州区GDP以2734.8亿元跃居浙江省各县(市)区第一，将该数用科学记数法表示是（）

A、2734.8x 10⁸ B、2.7348x10¹¹ C、2.7348x 10¹² D、0.27348x10¹³

查看试题解析
4. 要使分式 $\frac{x - 1}{x + 1}$ 有意义，则x的取值范围是（）

A、x≠-1 B、x≠1 C、x≠士1 D、x≠0

查看试题解析
5. 某志愿者小分队年龄情况如下，则这12名队员年龄的众数、中位数分别是（）

年龄（岁）

19

20

21

23

人数（名）

2

5

2

2

1

A、2名，20岁 B、5名，20岁 C、20岁，20岁 D、20岁，20.5岁

查看试题解析
6. 如图，量得一个纸杯的高为11cm， 6个叠放在一起的纸杯高度为 13.5cm，则10个纸杯
叠放在一起的高度是（）

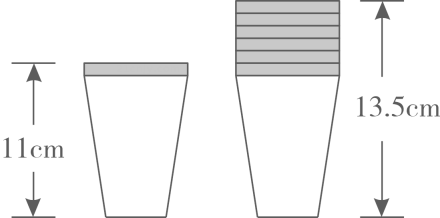A、15cm B、15.5cm C、1 6cm D、l6.5cm

查看试题解析
7. 某业主贷款9万元购进一台机器生产甲，乙两种产品、已知甲产品的销售净利润是每个5元，乙产品的销售净利润是每个6元，2个甲产品和1个乙产品组成一套销售，设销售套能赚回这台机器的贷款，则x满足的关系是（）

A、2X 5x+6x≥90000 B、2X 5x+6x≤90000 C、2(5.x+6.x)≥ 90000 D、2(5x+6x)≤90000

查看试题解析
8. 如图，Rt△ABC中， ∠ACB=90°，∠A=30°，CD⊥AB于D，CE是△ABC的中线，要说明“三个角分别对应相等的两个三角形全等”是假命题，可以作为反例的两个三角形是（）

A、△ACE和△BCE B、△BCE和△ABC C、△CDE 和△BCD D、△ACD和△BCD

查看试题解析
9. 如图，在平面直角坐标系中，点A，B分别在反比例函数y= $\frac{k_{1}}{x}$ ( $k_{1}$ >0， x>0) ，y= $\frac{k_{2}}{x}$ ( $k_{2}$ <0， x<0)的图象上，连结AB交y轴于点C，作点B关于x轴的对称点D，连结AD恰好经过坐标原点O，若 $\frac{A C}{B C} = \frac{3}{2}$ ，则 $\frac{k_{1}}{k_{2}}$ 的值为（）.

A、 $\frac{3}{2}$ B、- $\frac{3}{2}$ C、 $\frac{9}{4}$ D、- $\frac{9}{4}$

查看试题解析
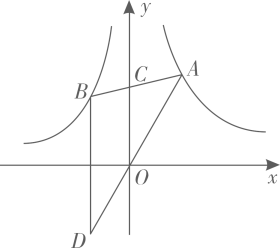10. 如图，4个全等的直角三角形围出一个正方形 ABCD，过点P， Q分别作AC的平行线，过点M， N分别作BD的平行线得四边形EFGH.若已知正方形ABCD的面积，则直接可求的量是（）

A、线段MH的长 B、△AMQ的周长 C、线段GN的长 D、四边形EFGH的面积

查看试题解析

二、填空题(每小题5分，共30分)

11. 实数8的立方根是．

查看试题解析
12. 在一个不透明的袋子里装着1个白球、3个黄球、4个红球，它们除颜色不同外其余都相同.现从袋中任意摸出一个球是黄球的概率为.

查看试题解析
13. 底面半径为5cm，母线长为13cm的圆锥的侧面积为 cm².

查看试题解析
14. 如图，二次函数y=ax²+bx+c (a≠0)图象经过点A(-1，-2)，对称轴为直线x=1，则9a+3b+c的值是.

查看试题解析
15. 如图，△ABC中，∠BAC=35° ，边BC与以AB为直径的⊙O相切于点B，将△ABC绕点A顺时针旋转，记旋转角度为a (0°<a<180)，旋转过程中，△ABC 的边与⊙O相切时，a的值为.

查看试题解析
16. 如图，Rt△ABC中，∠C=90° ，AC=BC=8，作正方形CDEF，其中顶点E在边AB上.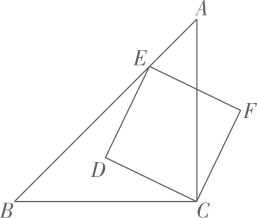

(1)、若正方形CDEF的边长为2 $\sqrt{6}$ ，则线段AE的长是

(2)、若点D到AB的距离是 $\sqrt{2}$ ，则正方形CDEF的边长是.

查看试题解析

三、解答题(第17~19题各8分，第20~22题各10分，第23题12分，第24题14分，共80分)

17.

(1)、计算： $2^{- 1} - | - \frac{1}{2} | + {(π - 2023)}^{0}$ ；

(2)、解方程组： ${\begin{cases} x - 2 y = 10 \\ 2 x + y = - 5 \end{cases}$ .

查看试题解析
18. 如图，是由边长为1的小正方形构成的5X4的网格图.请仅用无刻度的直尺，在给定的网格中，分别按下列要求画图，保留适当的画图痕迹.

(1)、在图1中画一个平行四边形，要求一条边长为 $\sqrt{5}$ 且面积为8； .

(2)、在图2中画一个矩形，要求一条边长为 $\sqrt{5}$ 且面积为10 .

查看试题解析
19. 观察两个连续偶数的平方差：
①4²-2²=12，②6²-4²=20，③8²-6²=28，.... ....

(1)、写出第n个等式，并进行证明；

(2)、问172是否可以写成两个连续偶数的平方差?如果能，请写出这两个偶数：如果不能，请说明理由.

查看试题解析
20. 某校在全校范围内随机抽取了一些学生进行“我最喜欢的球类运动”调查，将调查结果整理后绘制如下两幅不完整的统计图.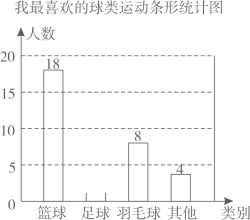

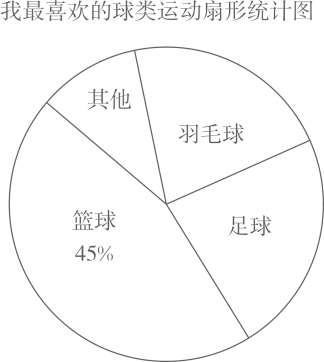
请根据图中的信息，解答下列各题：

(1)、在本次调查中，一共抽取了名学生，在扇形统计图中，羽毛球对应的圆心角为度；

(2)、请补全条形统计图；

(3)、统计发现，该校“最喜欢篮球”的人数与“最喜欢足球”人数大约相差240人，请估计全校总人数.

查看试题解析
21. 如图1，是一个自动伸缩晾衣架的实物图，图2是它的支架左侧平面示意图，当C， D在上滑槽MN.上左右滑动时，A， B同时在与MN平行的下滑槽EF上滑动，带动整个支架改变菱形内角度数，从而调节支架的高度，图2中PA=PB=OC=OD=15cm，中间7个菱形的边长均为15cm.

(1)、当∠APB调节至120°时，求两滑槽间的距离(即MN与EF之间的距离)；

(2)、根据生活经验，当一个身高160cm的人，头顶与下滑槽EF的距离不超过30cm时，
晒衣服比较方便，若上滑槽MN距离地面270cm，那么∠ABP至少调整到多少度?(参考数据： sin19.5° =0.33， cos70.5° =0.33， tan70.5° =2.82)

查看试题解析
22. 如图1，有一块边角料ABCDE，其中AB，BC， DE， EA是线段，曲线CD可以看成反比例函数图象的一部分.小宁想利用这块边角料截取一个面积最大的矩形MNQP，其中M，N在AE上(点M在点N左侧)，点P在线段BC上，点Q在曲线CD. 上.测量发现：
∠A=∠E=90°，AE=5，AB=DE=1，点C到AB，AE所在直线的距离分别为2，4.

(1)、小宁尝试建立坐标系来解决该问题，通过思考，他把A，B， C， D， E这5个点.先描到平面直角坐标系上，记点A的坐标为(-1， 0)；点B的坐标为(-1， 1) .
请你在图2中补全平面直角坐标系并画出图形ABCDE；

(2)、求直线BC，曲线CD的解析式；

(3)、求矩形MNQP的最大面积.

查看试题解析
23.

(1)、【基础巩固】
如图1，四边形ABCD中，AC平分∠BAD， AB=AD.
求证：∠ACB=∠ACD；

(2)、【迁移运用】
如图2，在(1)的条件下，取AB的中点E，连结DE交AC于点F，若∠AFE=∠ACD，EF=2 $\sqrt{3}$ ，求DF的长；

(3)、【解决问题】
如图3，四边形ABCD中，AD=CD，∠ADC =90°，在BC上取点E，使得DE=DC，恰有BE=AB.若AD=3 $\sqrt{10}$ ， CE=6，求四边形ABCD的面积.

查看试题解析
24. 如图1，圆O的直径AB垂直弦CD于点E，点P为弧AC上的一点，连结PE并延长交圆O于点Q，连结DQ，过点P画PF∥DQ交DC的延长线于点F，若圆O的直径为10， OE=3.

(1)、求CD的长；

(2)、如图2，当∠PQD=90°时，求∠PEC的正切值；

(3)、如图1，设PE=x， DF=y.
①求y关于x的函数解析式；②若PF×DQ=20，求y的值.

查看试题解析

年龄（岁）	19	20	21		23
人数（名）	2	5	2	2	1