浙江省湖州市吴兴区2022-2023学年七年级下学期数学期中试题
试卷更新日期:2023-05-12 类型:期中考试
一、选择题(本大题共10小题,共30分)
-
1. 下列方程是二元一次方程的是( )A、y=x B、x+ =2 C、xy=6 D、x﹣y=z﹣52. 下列计算中,正确的是( )A、m2•m3=m6 B、(m3)2=m5 C、m+m2=2m3 D、﹣m3+3m3=2m33. 已知1微米=10﹣7米,则25微米用科学记数法表示为( )A、0.25×10﹣5米 B、25×10﹣7米 C、2.5×10﹣6米 D、2.5×10﹣8米4. 如图,∠1和∠2是同位角的是( )A、
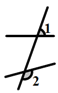 B、
B、 C、
C、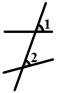 D、
D、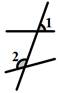 5. 二元一次方程有无数个解,下列四组值中是该方程的解的是( )A、 B、 C、 D、6. 下列多项式乘法中,能用平方差公式计算的是( )A、 B、(-m-n)(m+n) C、(-m-n)(m-n) D、(m-n)(n-m)7. 如图,下列条件中,不能判定AB∥CD的是( )
5. 二元一次方程有无数个解,下列四组值中是该方程的解的是( )A、 B、 C、 D、6. 下列多项式乘法中,能用平方差公式计算的是( )A、 B、(-m-n)(m+n) C、(-m-n)(m-n) D、(m-n)(n-m)7. 如图,下列条件中,不能判定AB∥CD的是( ) A、∠D+∠BAD=180° B、∠1=∠2 C、∠B=∠DCE D、∠3=∠48. 一副直角三角板如图放置,点C在FD的延长线上, , , , , 则为( )
A、∠D+∠BAD=180° B、∠1=∠2 C、∠B=∠DCE D、∠3=∠48. 一副直角三角板如图放置,点C在FD的延长线上, , , , , 则为( ) A、10° B、15° C、25° D、30°9. 如图(1),从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后,将剩余的部分剪拼成一个长方形,如图(2),通过计算阴影部分的面积可以得到( )
A、10° B、15° C、25° D、30°9. 如图(1),从边长为a的大正方形的四个角中挖去四个边长为b的小正方形后,将剩余的部分剪拼成一个长方形,如图(2),通过计算阴影部分的面积可以得到( ) A、(a-2b)2=a2-4ab+b2 B、(a+2b)2=a2+4ab+b2 C、(a-2b)(a+2b)=a2-4b2 D、(a+b)2=a2+2ab+b210. 现有如图①的小长方形纸片若干块,已知小长方形的长为a,宽为b.用3个如图②的图形和8个如图①的小长方形,拼成如图③的大长方形,若大长方形的宽为30cm,则图③中阴影部分面积与整个图形的面积之比为( ).
A、(a-2b)2=a2-4ab+b2 B、(a+2b)2=a2+4ab+b2 C、(a-2b)(a+2b)=a2-4b2 D、(a+b)2=a2+2ab+b210. 现有如图①的小长方形纸片若干块,已知小长方形的长为a,宽为b.用3个如图②的图形和8个如图①的小长方形,拼成如图③的大长方形,若大长方形的宽为30cm,则图③中阴影部分面积与整个图形的面积之比为( ).
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共24分)
-
11. 因式分解:a2-a= .12. 在方程4x﹣2y=7中,如果用含有x的式子表示y,则y= .13. 已知an=2,bn=6,则a4n•b2n的值为 .14. 若(x2-x+1)(x-q)的乘积中不含x2项,则q= .15. 如图,将一块长方形纸条折成如图的形状,若已知∠1=70°,则∠2的度数为.
 16. 若关于x、y的二元一次方程组 ,的解是 ,则关于a、b的二元一次方程组 的解是 .
16. 若关于x、y的二元一次方程组 ,的解是 ,则关于a、b的二元一次方程组 的解是 .三、解答题(本大题共8小题,共66分)
-
17. 计算(1)、-12023+(2)、18. 解方程组(1)、(2)、19. 如图,OC是∠AOB的平分线,且∠1=∠2,试说明EF∥OB的理由.
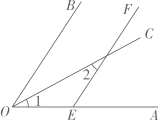 20. 先化简,再求值: ,其中 .21. 在网格上,平移△ABC,并将△ABC的一个顶点A平移到点D处,
20. 先化简,再求值: ,其中 .21. 在网格上,平移△ABC,并将△ABC的一个顶点A平移到点D处,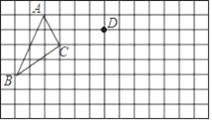 (1)、请你作出平移后的图形△DEF;(2)、请求出△DEF的面积(每个网格是边长为1的正方形).22. 随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元。(1)、求A、B两种型号的汽车每辆进价分别为多少万元?(2)、若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案.23. 数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)、请你作出平移后的图形△DEF;(2)、请求出△DEF的面积(每个网格是边长为1的正方形).22. 随着“低碳生活,绿色出行”理念的普及,新能源汽车正逐渐成为人们喜爱的交通工具.某汽车销售公司计划购进一批新能源汽车尝试进行销售,据了解2辆A型汽车、3辆B型汽车的进价共计80万元;3辆A型汽车、2辆B型汽车的进价共计95万元。(1)、求A、B两种型号的汽车每辆进价分别为多少万元?(2)、若该公司计划正好用200万元购进以上两种型号的新能源汽车(两种型号的汽车均购买),请你帮助该公司设计购买方案.23. 数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.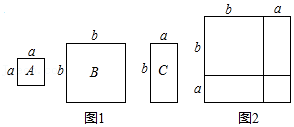 (1)、请用两种不同的方法求图2大正方形的面积:
(1)、请用两种不同的方法求图2大正方形的面积:方法1:;方法2:;
(2)、观察图2,请你写出代数式:(a+b)2 , a2+b2 , ab之间的等量关系 ;(3)、根据(2)题中的等量关系,解决如下问题:①已知:a+b=5,(a-b)2=13,求ab的值;
②已知(2023-a)2+(a-2022)2=5,求(2023-a)(a-2022)的值.
24. 已知:AB∥CD,E、G是AB上的点,F、H是CD上的点,∠1=∠2. (1)、如图1,求证:EF∥GH;(2)、如图2,过F点作FM⊥GH交GH延长线于点M,作∠BEF、∠DFM的角平分线交于点N,EN交GH于点P,求证:∠N=45°;(3)、如图3,在(2)的条件下,作∠AGH的角平分线交CD于点Q,若3∠FEN=4∠HFM,请你求出的值.
(1)、如图1,求证:EF∥GH;(2)、如图2,过F点作FM⊥GH交GH延长线于点M,作∠BEF、∠DFM的角平分线交于点N,EN交GH于点P,求证:∠N=45°;(3)、如图3,在(2)的条件下,作∠AGH的角平分线交CD于点Q,若3∠FEN=4∠HFM,请你求出的值.