人教版2022-2023学年度第二学期七年级数学 一元一次不等式组 期末复习
试卷更新日期:2023-05-12 类型:复习试卷
一、单选题
-
1. 已知关于x的不等式组有四个整数解,则m的取值范围是( )A、 B、 C、 D、2. 不等式组的整数解有4个,则a的取值可能是( )A、1 B、2 C、-2 D、-33. 不等式组的解集在数轴上表示为( )A、
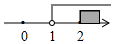 B、
B、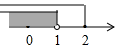 C、
C、 D、
D、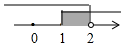 4. 已知不等式组解集为 , 则的值为( )A、1 B、2022 C、-1 D、-20225. 运行程序如图所示,规定:从“输入一个值x”到“结果是否95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )
4. 已知不等式组解集为 , 则的值为( )A、1 B、2022 C、-1 D、-20225. 运行程序如图所示,规定:从“输入一个值x”到“结果是否95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( ) A、 B、 C、 D、6. 若不等式组的解集为x>4,则a的取值范围是( )A、a>4 B、a<4 C、a≤4 D、a≥47. 若关于x,y的方程组的解x,y的值都小于1,则k的取值范围是( )A、-3<k<1 B、-3≤k<1 C、-3<k≤1 D、-3≤k≤18. 小华去商店购买、两种玩具,共用了12元,种玩具每件1元,种玩具每件3元.若每种玩具至少买一件,且种玩具的数量不少于种玩具的数量,则小华的购买方案有( )A、7种 B、6种 C、4种 D、3种9. 口味虾、臭豆腐、嗦螺和糖油粑粑是是长沙著名的小吃,某兴趣小组在班级发动了一项“舌尖上的长沙-我最喜欢的长沙小吃”调查活动,发现结果满足以下三个条件:、
A、 B、 C、 D、6. 若不等式组的解集为x>4,则a的取值范围是( )A、a>4 B、a<4 C、a≤4 D、a≥47. 若关于x,y的方程组的解x,y的值都小于1,则k的取值范围是( )A、-3<k<1 B、-3≤k<1 C、-3<k≤1 D、-3≤k≤18. 小华去商店购买、两种玩具,共用了12元,种玩具每件1元,种玩具每件3元.若每种玩具至少买一件,且种玩具的数量不少于种玩具的数量,则小华的购买方案有( )A、7种 B、6种 C、4种 D、3种9. 口味虾、臭豆腐、嗦螺和糖油粑粑是是长沙著名的小吃,某兴趣小组在班级发动了一项“舌尖上的长沙-我最喜欢的长沙小吃”调查活动,发现结果满足以下三个条件:、
(1)喜欢嗦螺的人数少于喜欢口味虾的人数;
(2)喜欢嗦螺的人数多于喜欢臭豆腐的人数;
(3)喜欢臭豆腐的人数的3倍多于喜欢口味虾的人数.若喜欢臭豆腐的人数为6,则喜欢嗦螺的人数的最大值为( )
A、16 B、6 C、17 D、710. 使得关于的不等式组有解,且使得关于的方程有非负整数解的所有的整数的个数是( )A、0个 B、1个 C、2个 D、3个二、填空题
-
11. 运行程序如图所示,规定:从“输入一个值x”到“结果是否>5”为一次程序操作,如果程序操作进行了两次才停止,那么x的取值范围是 .
 12. 已知不等式组的解集是 , 则关于的方程的解为.13. 人教版七年级下册数学课本共有如下6章内容:《相交线与平行线》、《实数》、《平面直角坐标系》、《二元一次方程组》、《不等式与不等式组》、《数据的收集、整理与描述》.若某期末试卷要求,每章至少有4个题,全卷总题数不超过26个题,设本期末试卷的全卷总题数为x个题,则x的取值范围是 .14. 如果不等式组 , 只有三个整数解,a的取值范围是 .15. 若整数a使关于x的不等式组 , 有且只有45个整数解,则a的值为 .
12. 已知不等式组的解集是 , 则关于的方程的解为.13. 人教版七年级下册数学课本共有如下6章内容:《相交线与平行线》、《实数》、《平面直角坐标系》、《二元一次方程组》、《不等式与不等式组》、《数据的收集、整理与描述》.若某期末试卷要求,每章至少有4个题,全卷总题数不超过26个题,设本期末试卷的全卷总题数为x个题,则x的取值范围是 .14. 如果不等式组 , 只有三个整数解,a的取值范围是 .15. 若整数a使关于x的不等式组 , 有且只有45个整数解,则a的值为 .三、解答题
-
16. 解不等式组, , 并把它的解集在数轴上表示出来.17. x取哪些整数值时,不等式与都成立?18. 解不等式组 , 并把解集在数轴上表示,同时判断是否是该不等式组的解.
四、综合题
-
19. 某公司要将一批防疫物资运灾区,计划租用A、B两种型号的货车.在每辆货车都满载的情况下,若租用15辆A型货车和25辆B型货车可装载750箱防疫物资;若租用10辆A型货车和30辆B型货车可装载700箱防疫物资.(1)、A、B两种型号的货车每辆分别可装载多少箱防疫物资;(2)、初步估算,公司要运输的这批防疫物资不超过1245箱.计划租用A、B两种型号的货车共70辆,且B型货车的数量不超过A型货车数量的3倍,该公司一次性将这批防疫物资运往灾区共有几种租车方案?20. 如图,“开心”农场准备用的护栏围成一块靠墙的长方形花园,设长方形花园的长为 , 宽为 .
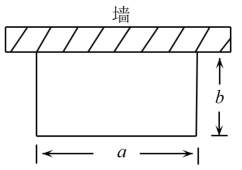 (1)、写出用b表示a的式子a= . 当时,求b的值;(2)、受场地条件的限制,a的取值范围为 , 求b的取值范围.21.(1)、解下列方程组:;(2)、解不等式组: , 并把解集在数轴上表示出来.
(1)、写出用b表示a的式子a= . 当时,求b的值;(2)、受场地条件的限制,a的取值范围为 , 求b的取值范围.21.(1)、解下列方程组:;(2)、解不等式组: , 并把解集在数轴上表示出来. 22. 现定义运算“”,对于任意有理数、 , 都有 , 例如: , 请根据上述知识解决问题:(1)、化简:;(2)、若(1)的代数式值大于而小于9,求的取值范围.23. 在城市创卫工作中为“保护好环境,拒绝冒黑烟”,某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车3辆,B型公交车2辆,共需600万元;若购买A型公交车2辆,B型公交车3辆,共需650万元.(1)、求购买A型和B型公交车每辆各需多少万元?(2)、预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
22. 现定义运算“”,对于任意有理数、 , 都有 , 例如: , 请根据上述知识解决问题:(1)、化简:;(2)、若(1)的代数式值大于而小于9,求的取值范围.23. 在城市创卫工作中为“保护好环境,拒绝冒黑烟”,某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车3辆,B型公交车2辆,共需600万元;若购买A型公交车2辆,B型公交车3辆,共需650万元.(1)、求购买A型和B型公交车每辆各需多少万元?(2)、预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?