人教版2022-2023学年度第二学期七年级数学 不等式 期末复习
试卷更新日期:2023-05-12 类型:复习试卷
一、单选题
-
1. 关于x的一元一次不等式x-3<0的解集在数轴上表示为( )A、
 B、
B、 C、
C、 D、
D、 2. 不等式的解集在数轴上表示正确的是( )A、
2. 不等式的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 3. 不等式组 , 的解集是( )A、x>0 B、x>2 C、x≥-1 D、x≤-14. 不等式的解集在数轴上表示正确的是( )A、
3. 不等式组 , 的解集是( )A、x>0 B、x>2 C、x≥-1 D、x≤-14. 不等式的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、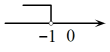 5. 若关于的不等式组的解集是 , 则的取值范围是A、 B、 C、 D、6. 若 , 那么下列各式中正确的是( )A、 B、 C、 D、7. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、8. 若 , 则下列不等式变形错误的是( )A、 B、 C、 D、9. 已知点在直线上,且 , 则下列不等关系一定成立的是( )A、 B、 C、 D、10. 若 , 且 , 异号,则的符号为( )A、大于 B、小于 C、大于等于 D、小于等于
5. 若关于的不等式组的解集是 , 则的取值范围是A、 B、 C、 D、6. 若 , 那么下列各式中正确的是( )A、 B、 C、 D、7. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、8. 若 , 则下列不等式变形错误的是( )A、 B、 C、 D、9. 已知点在直线上,且 , 则下列不等关系一定成立的是( )A、 B、 C、 D、10. 若 , 且 , 异号,则的符号为( )A、大于 B、小于 C、大于等于 D、小于等于二、填空题
-
11. 写出一个解为且一次项系数大于3的一元一次不等式.12. 不等式组的解集为 , 则m的取值范围为 .13. 用“”或“”填空:若 , 则+1+1.14. 用“>”或“<”填空:若 , 则ab.15. 若整数满足 , 则的值是.
三、解答题
-
16. 解不等式 , 并把它的解集在数轴上表示出来.17. 若不等式组的解集为-1<x<1,求(a+1)(b-1)的值.18. 若x<y,且(a-3)x>(a-3)y,求a的取值范围.
四、综合题
-
19. 解下列不等式,并把解集在数轴上表示出来.(1)、(2)、;20. 为了更好地打造生态文明城,桃源社区计划用公益基金购进甲、乙两种体育器材供市民锻炼身体.调查发现:若购买甲种体育器材3个,乙种体育器材2个,共需要资金1.2万元;若购买甲种体育器材4个,乙种体育器材3个,共需要资金1.7万元.(1)、甲、乙两种体育器材的单价分别是多少万元?(2)、若该社区计划购进这两种体育器材共20个,而最多提供公益基金4.8万元,甲种体育器材至少购进多少个?21. 当时,(1)、请比较与的大小,并说明理由.(2)、若 , 则的取值范围为直接写出答案22. 阅读材料:若点 , 在数轴上分别表示实数 , , 那么 , 之间的距离可表示为.例如 , 即表示3,1在数轴上对应的两点之间的距离;同样:表示5,在数轴上对应的两点之间的距离.根据以上信息,完成下列题目:(1)、已知 , , 为数轴上三点,点对应的数为 , 点对应的数为1.
①若点对应的数为 , 则 , 两点之间的距离为 ;
②若点到点的距离与点到点的距离相等,则点对应的数是 .
(2)、对于这个代数式.①它的最小值为 ;
②若 , 则的最大值为 .
23. 【阅读】根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:若 , 则;
若 , 则;
若 , 则.
反之也成立.
这种比较大小的方法称为“作差法比较大小”.
(1)、【理解】若 , 则(填“”、“”或“”)(2)、【运用】若 , , 试比较 , 的大小.(3)、【拓展】请运用“作差法比较大小”解决下面这个问题.制作某产品有两种用料方案,方案一:用5块A型钢板,6块型钢板.方案二:用4块A型钢板,7块型钢板.每块A型钢板的面积比每块型钢板的面积小.方案一的总面积记为 , 方案二的总面积记为 , 试比较 , 的大小.