人教版2022-2023学年度第二学期七年级数学 坐标方法的简单应用 期末复习

试卷更新日期：2023-05-11 类型：复习试卷

进入 出卷网 下载

一、单选题

  • 1. 2022年6月5日神舟十四号载人飞船在甘肃酒泉发射升空，航天员乘组在轨工作生活6个月后于2022年12月4日返回地球，下列描述能确定飞船着陆位置的是（ ）
    A、内蒙古中部 B、酒泉卫星发射中心东北方向800km处 C、东经130°25'~98°10' D、北纬54°35'~38°20'

    查看试题解析

  • 2. 如图所示，每个小方格的边长都为1，在直角坐标系中，如果图书馆的横坐标与实验楼的横坐标互为相反数，大门的纵坐标与实验楼的纵坐标互为相反数，则图书馆的坐标是（   ）

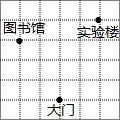    A、（1，5） B、（﹣2，3） C、（﹣2，﹣1） D、（﹣2，1）

    查看试题解析

  • 3. 2019年4月29日中国北京世界园艺博览会在北京延庆开幕，大会以“绿色生活，美丽家园”为主题．如图是北京世界园艺博览会园内部分场馆的分布示意图，在图中，分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系，如果表示国际馆的点的坐标为(4 ， 2) ， 表示植物馆的点的坐标为(−6 ， −1) ， 那么下列各场馆的坐标表示正确的是（       ）

    A、中国馆的坐标为(0 ， 1) B、水宇阁的坐标为(−3 ， 2) C、演艺中心的坐标为(1 ， 5) D、生活体验馆的坐标为(6 ， 6)

    查看试题解析

  • 4. 如图是天安门周围的景点分布示意图．在图中，分别以正东，正北方向为x轴，y轴的正方向建立平面直角坐标系．如果表示景山的点的坐标为(0，4)，表示王府井的点的坐标为(3，1)，则表示人民大会堂的点的坐标为（）

    A、(3，2) B、(-1，2) C、(-1，-1) D、(-1，-2)

    查看试题解析

  • 5. 周末，丽丽与欣欣相约一起到图书馆看书，下图是她俩在微信中的一段对话：

    根据上面两人的对话记录，丽丽能从A超市走到图书馆门口的路线是（       ）

    A、向北直走500米，再向西直走100米 B、向南直走500米，再向西直走100米 C、向北直走300米，再向西直走200米 D、向南直走300米，再向西直走200米

    查看试题解析

  • 6. 如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1 ， 则（       ）

    A、a=1 ， b=1 B、a=−1 ， b=−1 C、a=2 ， b=2 D、a=−2 ， b=−2

    查看试题解析

  • 7. 已知平面直角坐标系中，O为坐标原点，点A(−5 ， 4) ， B(x ， y) ， 将线段AB平移，使A与O重合，此时B点的对应点B'坐标为（2，-1），则B点的坐标是（ ）
    A、(7 ， −5) B、(3 ， −3) C、(−3 ， 3) D、(−7 ， 5)

    查看试题解析

  • 8. 如图，第二象限有两点A(m+3 ， n) ， B(m ， n−2) ， 将线段AB平移，使点A，B分别落在两条坐标轴上，则平移后点B的对应点的坐标是（  ）

    A、(3 ， 0)或(0 ， 2) B、(−3 ， 0)或(0 ， 2) C、(−3 ， 0)或(0 ， −2) D、(3 ， 0)或(0 ， −2)

    查看试题解析

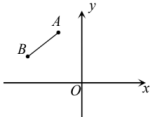  • 9. 如图，点A，B分别在y轴，x轴的正半轴上，且 OA=2OB=2 ，将线段AB平移得线段DC， C(m+n ， m+n2) ， D(m ， 72) ，则点 (m ， n) 位于（   ）

    A、直线BC下方区域 B、第四象限内 C、三角形ABC内部 D、三角形ABD内部

    查看试题解析

  • 10. 如图，△OAB的边OB在x轴的正半轴上，点B的坐标为（3，0），把△OAB沿x轴向右平移2个单位长度，得到△CDE，连接AC，DB，若△DBE的面积为3，则图中阴影部分的面积为（  ）

    A、32 B、1 C、2 D、12

    查看试题解析

二、填空题

  • 11. 王东的座位是3排4列，简记为(3 ， 4) ， 张三的座位是5排2列，可简记为.

    查看试题解析

  • 12. 如图是故宫部分建筑的分布示意图，分别以正东、正北方向为x轴，y轴的正方向建立平面直角坐标系．若慈宁宫的坐标为（－2，－2），紫禁城角楼的坐标为（3，1），那么太和殿的坐标为 ．

    查看试题解析

  • 13. 某校教学楼在校门的正北200m处，实验楼在教学楼正西100m处，若实验楼的坐标为(−100 ， 0) ， 则校门的坐标为 ．

    查看试题解析

  • 14. 线段AB平移后得到CD ， 已知A(2 ， 3)的对应点为C(−1 ， 4) ， 则B(3 ， 2)的对应点D的坐标为 ．

    查看试题解析

  • 15. 将点B (-3， 2)先向右平移m个单位长度，再向上平移n个单位后得到点B.(-1，5)，则mn的值为

    查看试题解析

三、解答题

  • 16.  如图，将△ABC向左平移6个单位长度，再向下平移4个单位长度，可以得到△A1B1C1 ， 画出平移后的△A1B1C1

    ①直接写出△A1B1C1各个顶点的坐标；

    ②写出S△ABC=      ▲      .

    查看试题解析

  • 17. 写出如图中△ABC各顶点的坐标且求出此三角形的面积.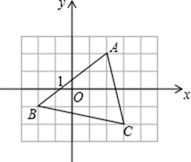

    查看试题解析

  • 18. 如图所示，在平面直角坐标系中，点A，B的坐标分别为A(a，0)，B(b，0)，且a，b满足|a+2|+ b−4 =0，点C的坐标为(0，3)。

    (1)、求a，b的值及S三角形ABC；
    (2)、若点Ｍ在x轴上，且S三角形ACM= 13 S三角形ABC ， 试求点Ｍ的坐标。

    查看试题解析

四、综合题

  • 19. 三角形AOB在平面直角坐标系中的位置如图所示．

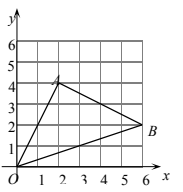    (1)、写出A、B两点的坐标；
    (2)、经过平移后，三角形AOB中任意一点P(x0 ， y0)的对应点为P1(x0+3 ， y0−2) ， 写出A、B两点的对应点A1、B1的坐标．
    (3)、求出三角形AOB的面积．

    查看试题解析

  • 20. 在平面直角坐标系中，三角形ABC经过平移得到三角形A'B'C' ， 位置如图所示．

    (1)、分别写出点A ， A'的坐标：A（ ， ），A'（ ， ）．
    (2)、请说明三角形A'B'C'是由三角形ABC经过怎样的平移得到的；
    (3)、若点M(m ， 4−n)是三角形ABC内部一点，则平移后对应点M'的坐标为(2n−8 ， m−4) ， 求m和n的值．

    查看试题解析

  • 21. 如图，在平面直角坐标系中，将点A(−1 ， 0)向右平移4个单位得到点B，将线段AB向上平移m个单位，再向右平移1个单位得到线段CD（点A与点D对应，点B与点C对应），且四边形ABCD的面积为8.

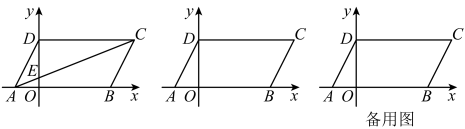    (1)、求点B，C的坐标；
    (2)、连接AC与y轴交于点E，求DEOE的值：
    (3)、若点P从O点出发，以每秒t个单位的速度向上平移运动，同时点Q从B点出发，以每秒2t个单位的速度向左平移运动，当点P到达点D后停止运动，若射线CQ交y轴于点F，设△CFP与△OFQ的面积差为S，问：S是否定值？如果S是定值，请求出它的值：如果S不是定值，请说明理由.

    查看试题解析

  • 22. 如图，在平面直角坐标系xOy中，已知A(8 ， 0) ， 将线段OA平移至CB ， 点D在x轴正半轴上，C(a ， b) ， 且a+b−10+|b−6|=0.连接OC ， AB ， CD ， BD.

    (1)、求出点C和点B的坐标；
    (2)、当△ODC的面积是△ABD的面积的3倍时，求点D的坐标；
    (3)、设∠OCD=α ， ∠DBA=β ， ∠BDC=θ ， 判断α、β、θ之间的数量关系，并说明理由.

    查看试题解析

  • 23. 如图，在直角坐标系中，点A(0 ， a) ， B(b ， 0)分别在y轴，x轴上，且|a−6|+8−b=0 ． AC⊥y轴，CB⊥x轴，AC ， CB交于点C ， D为OB的中点．

    (1)、求点C的坐标．
    (2)、点Q(x ， y)是线段CD上一点（不与点C ， D重合），用含x的式子表示y并求整点（横、纵坐标均为整数）Q的坐标．
    (3)、点P在OA上（点P不与O ， A重合），CP⊥EP ， 交OB于点E ， ∠ACP ， ∠OEP的平分线交于点F ． 当点P在线段OA上运动时，∠CFE的大小是否变化？若不变，求出∠CFE的度数；若变化，说明理由．

    查看试题解析