人教版2022-2023学年度第二学期七年级数学实数期末复习

试卷更新日期：2023-05-11 类型：复习试卷

进入出卷网下载

一、单选题

1. 设实数 $\sqrt{3}$ 的整数部分为m，小数部分为n，则（2m+n）（2m-n）的值是（）

A、 $2 \sqrt{3}$ B、 $- 2 \sqrt{3}$ C、 $2 \sqrt{3} - 2$ D、 $2 - 2 \sqrt{3}$

查看试题解析
2. 在实数 $- \frac{π}{2}$ ， 0， $\sqrt{2}$ ， $- 1$ 中，最小的是（）

A、 $- \frac{π}{2}$ B、0 C、 $\sqrt{2}$ D、 $- 1$

查看试题解析
3. 在 $\frac{33}{17}$ ， $\sqrt{3}$ ， $- \sqrt[3]{8}$ ， $π$ ， $2023$ 这五个数中，无理数的个数为（）

A、2 B、3 C、4 D、5

查看试题解析
4. 估计 $\sqrt{12} \times \sqrt{2}$ 的值应在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
5. 一只蚂蚁趴在如图所示的数轴上，它从点A沿数轴向右爬行2个单位长度到达点B，设点A表示 $- \sqrt{2}$ ，那么点B所表示的数为（）

A、 $2 + \sqrt{2}$ B、 $2 - \sqrt{2}$ C、 $- 2 + \sqrt{2}$ D、 $- 2 - \sqrt{2}$

查看试题解析
6. 下列实数中，最大的是（）

A、2 B、 $- \frac{1}{2}$ C、 $\sqrt{2}$ D、0

查看试题解析
7. 下列四个实数中，相反数最小的数是（）

A、 $- 1$ B、 $0$ C、 $\sqrt{5}$ D、 $- \frac{1}{3}$

查看试题解析
8. 如图，边长为1的正方形 $A B C D$ ， $A B$ 在数轴上，点A在原点，点B对应的实数1，以A为圆心， $A C$ 长为半径逆时针画弧交数轴于点E，则点E对应的实数是（）

A、 $- 1 - \sqrt{2}$ B、 $- \sqrt{2}$ C、 $\sqrt{2}$ D、 $- 2 + \sqrt{2}$

查看试题解析
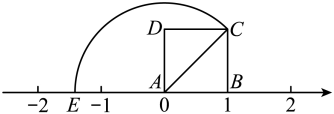9. 已知一个边长为a米的正方形，面积是37平方米，则a的取值范围是（）

A、4＜a＜5 B、5＜a＜6 C、6＜a＜7 D、7＜a＜8

查看试题解析
10. 已知实数a在数轴上的位置如图所示，则化简： $| a - 2 |$ + $\sqrt{{(a - 4)}^{2}}$ 的结果为（）

A、2 B、-2 C、2a-6 D、-2a+6

查看试题解析

二、填空题

11. 实数a、b在数轴上对应的点如图所示，则 $a + b$ 0.（填“ $>$ ”“ $<$ ”“ $=$ ”）

查看试题解析
12. 实数3.141， $^{3} \sqrt{- 27}$ ， π， $- \sqrt{2}$ ， $\frac{22}{7}$ ， 0.2，0.1010010001……中无理数有个 (填个数)．

查看试题解析
13. 在 $\sqrt{5}$ 与 $\sqrt{26}$ 之间，整数个数有个

查看试题解析
14. 若 $a + b = 2$ ，则称 $a$ 与 $b$ 是关于1的平衡数，那么 $5 - \sqrt{2}$ 关于1的平衡数是．

查看试题解析
15. 设n为正整数，且 $n < \sqrt{15} < n + 1$ ，则n的值为.

查看试题解析

三、解答题

16. 在如图所示的数轴上近似地表示下列各数，并用“<”连接．
$\frac{8}{3}$ ， 1.5， $- \sqrt{3}$ ， -π．

查看试题解析
17. 已知a为 $\sqrt{17}$ 的整数部分， $b - 1$ 是121的算术平方根，求 $\sqrt{a + b}$ 的值．

查看试题解析
18. 阅读下列材料：
∵ $\sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$ ， ∴ $\sqrt{7}$ 的整数部分为 $2$ ，小数部分为 $\sqrt{7} - 2$

请你观察上述的规律后，解答下面的问题：

如果 $\sqrt{6}$ 的小数部分为 $x$ ， $\sqrt{15}$ 小数部分为 $y$ ，求 $x + y - \sqrt{6} - \sqrt{15} - 3$ 的立方根．

查看试题解析

四、综合题

19. 阅读下面材料：．
∵ $\sqrt{4}$ < $\sqrt{6}$ < $\sqrt{9}$ ，即2< $\sqrt{6}$ <3，

∴ $\sqrt{6}$ 的整数部分为2，小数部分为 $\sqrt{6}$ -2．

请解答下列问题；

(1)、 $\sqrt{22}$ 的整数部分是，小数部分是；

(2)、已知7- $\sqrt{22}$ 的小数部分是m，7+ $\sqrt{22}$ 的小数部分是n，求m+n的值．

查看试题解析
20. 已知 $2 a - 1$ 的算术平方根是3， $3 a + b - 9$ 的立方根是2， $c$ 是 $\sqrt{57}$ 的整数部分.

(1)、求 $a ， b ， c$ 的值；

(2)、求 $a + 2 b + c$ 的平方根.

查看试题解析
21. 我们知道 $\sqrt{2}$ ≈1.414，于是我们说：“ $\sqrt{2}$ 的整数部分为1，小数部分则可记为 $\sqrt{2}$ -1”．则：

(1)、 $\sqrt{2}$ +1的整数部分是，小数部分可以表示为

(2)、已知 $\sqrt{3}$ +2的小数部分是a，7- $\sqrt{3}$ 的小数部分为b．那a+b=

(3)、已知 $\sqrt{11}$ 的整数部分为x， $\sqrt{11}$ 的小数部分为y，求(y- $\sqrt{11}$ )^x-1的平方根．

查看试题解析
22. 【材料】∵ $\sqrt{4} < \sqrt{6} < \sqrt{9}$ ，即 $2 < \sqrt{6} < 3$ ，∴ $\sqrt{6}$ 的整数部分为2，小数部分为 $\sqrt{6} - 2$ ．
【应用】

(1)、 $\sqrt{22}$ 的整数部分是，小数部分是；

(2)、已知 $7 - \sqrt{22}$ 的小数部分是 $m$ ， $7 + \sqrt{22}$ 的小数部分是 $n$ ，求 $m + n$ 的值．

查看试题解析
23. 阅读下面的文字，解答问题：
大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部地写出来，于是小明用 $(\sqrt{2} - 1)$ 来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．

又例如：

∵ $\sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$ ， ∴ $\sqrt{7}$ 的整数部分为2，小数部分为 $(\sqrt{7} - 2)$ ．

请解答：

(1)、 $\sqrt{21}$ 的整数部分是，小数部分是．

(2)、如果 $\sqrt{11}$ 的小数部分为a， $\sqrt{101}$ 的整数部分为b，求 $a + b - \sqrt{11}$ 的值；

(3)、已知： $10 + \sqrt{3} = x + y$ ，其中x是整数，且 $0 < y < 1$ ，求 $x - y$ 的值．

查看试题解析

人教版2022-2023学年度第二学期七年级数学 实数 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

人教版2022-2023学年度第二学期七年级数学实数期末复习