人教版2022-2023学年度第二学期七年级数学立方根期末复习

试卷更新日期：2023-05-11 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列各式中，正确的是（）

A、 $\sqrt{1 \frac{7}{9}} = \pm \frac{4}{3}$ B、 $^{3} \sqrt{27}$ =±3 C、 $\sqrt{(- 4)^{2}}$ =-4 D、± $\sqrt{121}$ =±11

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{8} = 4$ B、 $\sqrt[3]{64} = 4$ C、 $\sqrt{1 \frac{9}{16}} = 1 \frac{3}{4}$ D、 $\sqrt{36} = \pm 6$

查看试题解析
3. 已知甲、乙两个立方体，甲的体积是乙体积的8倍，则甲的棱长是乙的棱长的（）

A、8倍 B、2倍 C、4倍 D、 $\frac{1}{2}$ 倍

查看试题解析
4. 下列等式成立的是（）

A、 $\sqrt{49}$ =±7 B、 $\sqrt{(- 7)^{2}}$ =-7． C、( $^{3} \sqrt{- 7}$ )³=-7 D、( $- \sqrt{7}$ )²=-7

查看试题解析
5. 立方根为8的数是（）

A、512 B、64 C、2 D、 $\pm 2$

查看试题解析
6. 下列说法中，正确的是（）

A、11的平方根记作 $\sqrt{11}$ B、11的算术平方根记作 $\pm \sqrt{11}$ C、 $- 11$ 的算术平方根记作 $\sqrt{- 11}$ D、 $- 11$ 的立方根记作 $\sqrt[3]{- 11}$

查看试题解析
7. 已知， $\sqrt[3]{x - 1} = x - 1$ ，则x²-x的值为（）

A、0 或 1 B、0 或 2 C、0 或 6 D、0、2 或 6

查看试题解析
8. 下列说法中：①立方根等于本身的是-1，0，1；②平方根等于本身的数是0，1；③两个无理数的和一定是无理数；④实数与数轴上的点是一一对应的；⑤a与b两数的平方和表示为a²+b².其中错误的是（）

A、①② B、②③ C、②③④ D、③④⑤

查看试题解析
9. 下列各数 $\frac{\sqrt{2}}{2}$ ， 3.14， $\sqrt[3]{- 8}$ ， $8 1^{- \frac{3}{4}}$ ， -0.2020020002…（它的位数无限且相邻两个“2”之间“0”的个数依次加1个）， $2 . \overset{•}{4}$ ， $\sqrt{18}$ 中，无理数的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
10. 若一个正数m的两个平方根分别是3a＋2和a－10，则m的立方根为（）

A、－4 B、4 C、－2 D、2

查看试题解析

二、填空题

11. 已知2x+7y+1的算术平方根是6，8x+3y的立方根是5，则x+y的平方根为．

查看试题解析
12. 一个数的平方根和它的立方根相等，则这个数是．

查看试题解析
13. 8的立方根为x，4是 $y + 1$ 的一个平方根，则 $x - y =$ ．

查看试题解析
14. 若 ${(x - 1)}^{3} = 8$ ，则 $x$ 的值是．

查看试题解析
15. 计算： ${(\frac{3}{4})}^{\frac{1}{3}} \times {(\frac{1}{6})}^{\frac{1}{3}}$ ＝．

查看试题解析

三、解答题

16. 将半径为12 cm的实心铁球熔化，重新铸造出8个半径相同的实心小铁球，不计损耗，小铁球的半径是多少？(球的体积公式V= $\frac{4}{3}$ πR³ ，其中R是球的半径)

查看试题解析
17. 一个正方体的体积是16，另一正方体的体积是这个正方体体积的4倍，求另一个正方体的表面积．

查看试题解析
18. 已知 $M = \sqrt[m - 4]{m + 3}$ 是 $m + 3$ 的算术平方根， $N = \sqrt[2 m - 4 n + 3]{n - 2}$ 是 $n - 2$ 的立方根，求 $M - N$ 的立方根．

查看试题解析

四、综合题

19. 已知 $2 a - 1$ 的算术平方根是3， $3 a + b - 9$ 的立方根是2， $c$ 是 $\sqrt{57}$ 的整数部分.

(1)、求 $a ， b ， c$ 的值；

(2)、求 $a + 2 b + c$ 的平方根.

查看试题解析
20.

(1)、计算： $\sqrt{9}$ + $| 3 - π |$ - $\sqrt{{(- 3)}^{2}}$ ；

(2)、求3（x-1）³＝81中的x的值．

查看试题解析
21. 若64的立方根是m，m的平方根是n．

(1)、求m的值；

(2)、求 $\sqrt{m + n^{2}}$ 的值．

查看试题解析
22. 数轴上有A、B两点，A点表示的数为x，且 $x^{2} = 9$ ， B点表示的数为 $\frac{27}{8}$ 的立方根．

(1)、求x的值，B点表示的数．

(2)、求AB间的距离．

查看试题解析
23. 如图，在平面直角坐标系中，点A、B是x轴、y轴上的点，若3是 $a + 3$ 的立方根，也是 $a - 2 b + 1$ 的算术平方根，且 $O A = a$ ， $O B = b$ ，将点B向左平移18个单位长度得到点C．

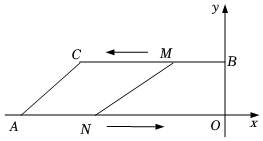(1)、求点A、B、C的坐标；

(2)、点M、N分别为线段BC、OA上的两个动点，点M从点B以1个单位长度/秒的速度向左运动，同时点N从点A以2个单位长度/秒的速度向右运动，设运动时间为t秒（ $0 \leq t \leq 12$ ）．
①当时 $B M = O N$ 时，求t的值；
②是否存在一段时间，使得 $S_{四边形 N A C M} < \frac{1}{2} S_{四边形 B O A C}$ ？若存在，求出t的取值范围；若不存在，请说明理由．

查看试题解析

人教版2022-2023学年度第二学期七年级数学 立方根 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

人教版2022-2023学年度第二学期七年级数学立方根期末复习