人教版2022-2023学年度第二学期七年级数学平行线的性质期末复习

试卷更新日期：2023-05-11 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，AB∥DE，BC⊥CD，则以下说法中正确的是（）

A、α，β的角度数之和为定值 B、α随β增大而增大 C、α，β的角度数之积为定值 D、α随β增大而减小

查看试题解析
2. 如图，把一块含有 $45 °$ 角的直角三角板的两个顶点放在直尺的对边上，如果 $∠ 2 = 21 °$ ，那么 $∠ 1$ 的度数是（）

A、 $21 °$ B、 $22 °$ C、 $23 °$ D、 $24 °$

查看试题解析
3. 如图，在四边形 $A B C D$ 中， $A B ∥ C D ， ∠ B A D = 9 0^{∘}$ ， $C E$ 平分 $∠ B C D$ ， $∠ C B F = 6 ∠ E B F$ ， $A G ∥ C E$ ，点H在直线 $C E$ 上，满足 $∠ F B H = ∠ D A G$ . 若 $∠ D A G = k ∠ E B H$ ，则k的值是（）

A、 $\frac{2}{3}$ 和 $\frac{7}{9}$ B、 $\frac{2}{3}$ 和 $\frac{3}{4}$ C、 $\frac{7}{5}$ 和 $\frac{7}{9}$ D、 $\frac{7}{5}$ 和 $\frac{3}{4}$

查看试题解析
4. 已知：如图，直线a，b被直线c所截，且a∥b，若∠1＝70°，则∠2的度数是（）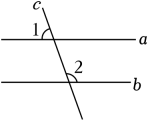

A、130° B、80° C、110° D、70°

查看试题解析
5. 如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1＝20°，那么∠2的度数是（）

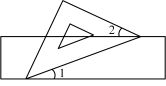A、30° B、25° C、20° D、15°

查看试题解析
6. 对于命题“如果 $a^{2} > b^{2}$ ，那么 $a > b$ ，下面四组关于 $a ， b$ 的值中，能说明这个命题是假命题的是（）

A、 $a = 4 ， b = - 3$ B、 $a = - 3 ， b = 4$ C、 $a = - 4 ， b = 3$ D、 $a = 4 ， b = 3$

查看试题解析
7. 下列命题中，是真命题的是（）

A、同位角相等 B、有且只有一条直线与已知直线垂直 C、相等的角是对顶角 D、邻补角一定互补

查看试题解析
8. 下列语句：
①若三条直线只有两个交点，则其中两条直线互相平行；②如果两条平行线被第三条所截，同旁内角相等，那么这两条平行线都与第三条直线垂直；③过一点有且只有一条直线与已知直线平行，其中（）

A、①②是真命题 B、②③是真命题 C、①③是真命题 D、以上结论皆是假命题

查看试题解析
9. 如图将一个直角三角板和一把直尺如图放置，如果∠α＝43°，则∠β的度数是（）

A、43° B、45° C、47° D、57°

查看试题解析
10. 如图，直线a，b被直线c所截，且a∥b．若∠1＝60°，则∠2的度数为（）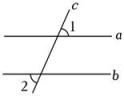

A、60° B、50° C、40° D、30°

查看试题解析

二、填空题

11. 某兴趣小组利用几何图形画出螳螂的简笔画，如图，已知 $∠ B A C = 130 °$ ， $A B / / D E$ ， $∠ D = 70 °$ ，则 $∠ A C D =$ .

查看试题解析
12. 如图，直线a，b被直线c所截，并且a∥b，若∠1＝108°，则∠2的度数是 .

查看试题解析
13. 如图， $A D$ 是 $∠ E A C$ 的平分线， $A D / / B C$ ， $∠ B = 30 °$ ，则 $∠ C =$ $° .$

查看试题解析
14. 若 $∠ α$ 与 $∠ β$ 的两边分别平行，且 $∠ α = (x + 20) °$ ， $∠ β = (3 x - 40) °$ ，则 $∠ α$ 的度数为.

查看试题解析
15. 命题“平行于同一条直线的两条直线平行”的题设是，结论是这两条直线平行。

查看试题解析

三、解答题

16. 如图，直线 $B C$ 与 $A F$ 相交于点 $E$ ， $A B / / C D$ ， $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ，求证： $A D / / B E$ .
证明： $∵ A B / / C D ($ 已知 $)$ ，
$∴ ∠ 4 = ∠ B A E$ （   ）
$∵ ∠ 3 = ∠ 4 ($ 已知 $)$ ，
$∴ ∠ 3 =$       ▲      （   ）
$∵ ∠ 1 = ∠ 2 ($ 已知 $)$ ，
$∴ ∠ 1 + ∠ C A F = ∠ 2 + ∠ C A F$ （   ）
即 $∠ B A E =$       ▲      .
$∴ ∠ 3 =$       ▲      （   ）
$∴ A D / / B E$ （   ）

查看试题解析
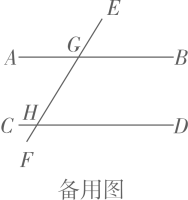
17. 如图，已知∠ABC+∠DCB=180°且∠1=∠2，试说明∠GFA+∠FDB=180°，请将下面的说明过程填写完整．

解：∵∠ABC+∠DCB=180°

∴CG∥AB，

∴∠1=∠FEA，（      ）

∵∠1=∠2，∴∠2=∠FEA，（      ）

∴EG∥      ▲ ，（      ）

∴      ▲ +∠FDB=180°，

∵∠GFA=∠DFE，（      ）

∴∠GFA+∠FDB=180°．

查看试题解析
18. 我们知道任何一个命题都由条件和结论两部分组成，如果我们把一个真命题的条件变结论，结论变条件，那么所得的命题是不是一个真命题？试举例说明．

查看试题解析

四、综合题

19. 已知， $∠ A B C$ 和 $∠ D E F$ 中， $A B / / D E$ ， $B C / / E F .$ 试探究：

(1)、如图1， $∠ B$ 与 $∠ E$ 的关系是；

(2)、如图2，写出 $∠ B$ 与 $∠ E$ 的关系，并说明理由.

查看试题解析
20. 如图，直线 $A B ∥ C D$ ，直线 $E F$ 与 $A B$ ， $C D$ 分别交于点 $G$ ， $H$ ， $∠ E H D = α (0 ° < α < 90 °)$ .小安将一个含 $30 °$ 角的直角三角板 $P M N$ 按如图①放置，使点 $N$ 、 $M$ 分别在直线 $A B$ 、 $C D$ 上，且在点 $C$ 、 $H$ 的右侧， $∠ P = 90 °$ ， $∠ P M N = 60 °$ .

(1)、填空； $∠ P N B + ∠ P M D$ $∠ P$ （填“ $>$ ”“ $<$ ”或“=” ）；

(2)、若 $∠ M N G$ 的平分线 $N O$ 交直线 $C D$ 于点 $O$ ，如图②.
①当 $N O ∥ E F$ ， $P M ∥ E F$ 时，求 $α$ 的度数；

②小安将三角板 $P M N$ 沿直线 $A B$ 左右移动，保持 $P M / / E F$ ，点 $N$ 、 $M$ 分别在直线 $A B$ 和直线 $C D$ 上移动，请直接写出 $∠ M O N$ 的度数（用含 $α$ 的式子表示）.

查看试题解析
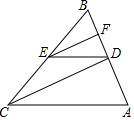
21. 如图，AF的延长线与BC的延长线交于点E，AD∥BE，∠1=∠2，∠3=∠4．

(1)、求证：AB∥DC；

(2)、若∠B=78°，∠E=25°，求∠CAE的度数．

查看试题解析
22. 如图，现有以下三个条件：① $A B / / C D ，$ ② $∠ B = ∠ C ，$ ③ $∠ E = ∠ F$ .请你以其中两个作为题设，另一个作为结论构造命题.

(1)、你构造的是哪几个命题？

(2)、你构造的命题是真命题还是假命题？若是真命题，请给予证明；若是假命题，请举出反例（证明其中的一个命题即可）.

查看试题解析
23. 如图，有如下四个论断：① $A C / / D E$ ， ② $D C / / E F$ ， ③ $C D$ 平分 $∠ B C A$ ， ④ $E F$ 平分 $∠ B E D$ ．

(1)、若选择四个论断中的三个作为条件，余下的一个论断作为结论，构成一个数学命题，其中正确的有哪些？不需说明理由．

(2)、请你在上述正确的数学命题中选择一个进行说明理由．

查看试题解析

人教版2022-2023学年度第二学期七年级数学 平行线的性质 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

人教版2022-2023学年度第二学期七年级数学平行线的性质期末复习