人教版2022-2023学年度第二学期七年级数学 相交线 期末复习
试卷更新日期:2023-05-11 类型:复习试卷
一、单选题
-
1. 如图各图中,∠1与∠2是对顶角的是( )A、
 B、
B、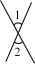 C、
C、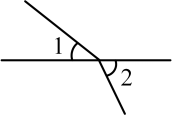 D、
D、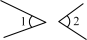 2. 如图,直线AB,CD相交于点O,OE⊥AB.若∠DOE=2∠AOC,则∠BOD的度数为( )
2. 如图,直线AB,CD相交于点O,OE⊥AB.若∠DOE=2∠AOC,则∠BOD的度数为( ) A、25° B、30° C、60° D、75°3. 小红在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线ln(n=1,2,3,4,5,6,7),其中l1、l2互相平行,l3、l4、I5三条直线交于一点,则他探究这7条直线的交点个数最多是( )A、17个 B、18个 C、19个 D、21个4. 如图,已知AB⊥BC,垂足为B,AB=3,点P是射线BC上的动点,则线段AP长不可能是( )
A、25° B、30° C、60° D、75°3. 小红在“趣味数学”社团活动中探究了直线交点个数的问题.现有7条不同的直线ln(n=1,2,3,4,5,6,7),其中l1、l2互相平行,l3、l4、I5三条直线交于一点,则他探究这7条直线的交点个数最多是( )A、17个 B、18个 C、19个 D、21个4. 如图,已知AB⊥BC,垂足为B,AB=3,点P是射线BC上的动点,则线段AP长不可能是( ) A、5 B、4 C、3 D、2.55. 如图,污水处理厂要从A处把处理过的水引入排水沟PQ,做法如下:过点A作AB⊥PQ于点B,沿着AB方向铺设排水管道可用料最省.能准确解释这一现象的数学知识是( )
A、5 B、4 C、3 D、2.55. 如图,污水处理厂要从A处把处理过的水引入排水沟PQ,做法如下:过点A作AB⊥PQ于点B,沿着AB方向铺设排水管道可用料最省.能准确解释这一现象的数学知识是( ) A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、过直线外一点有且只有一条直线与这条直线平行6. 如图,直线AB、CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=50°,则∠AOC= ( )
A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、过直线外一点有且只有一条直线与这条直线平行6. 如图,直线AB、CD相交于点O,OE⊥CD,垂足为点O.若∠BOE=50°,则∠AOC= ( )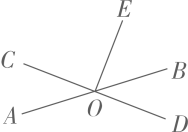 A、140° B、50° C、60° D、40°7. 如图,下列说法中不正确的是( )
A、140° B、50° C、60° D、40°7. 如图,下列说法中不正确的是( ) A、和是同旁内角 B、和是内错角 C、和是同位角 D、和是对顶角8. 仔细观察下列图形,其中∠1与∠2是内错角的是( )A、
A、和是同旁内角 B、和是内错角 C、和是同位角 D、和是对顶角8. 仔细观察下列图形,其中∠1与∠2是内错角的是( )A、 B、
B、 C、
C、 D、
D、 9. 张老师在黑板上画出如图所示的图形(已知 , , 垂足为),四位同学发表了自己的看法,与是同旁内角;与互相垂直;点到的垂线段是线段;点到的距离是线段 , 其中正确的看法有( )个.
9. 张老师在黑板上画出如图所示的图形(已知 , , 垂足为),四位同学发表了自己的看法,与是同旁内角;与互相垂直;点到的垂线段是线段;点到的距离是线段 , 其中正确的看法有( )个. A、4 B、3 C、2 D、110. 如图,直线a,b被c所截,则与是( )
A、4 B、3 C、2 D、110. 如图,直线a,b被c所截,则与是( ) A、同位角 B、内错角 C、同旁内角 D、邻补角
A、同位角 B、内错角 C、同旁内角 D、邻补角二、填空题
-
11. 如图,直线、相交于点O, , . 则 .
 12. 如图所示,已知直线 , 相交于O,平分 , , 则 .
12. 如图所示,已知直线 , 相交于O,平分 , , 则 . 13. 如图,于点O,平分 , 若 , 则 的度数为 .
13. 如图,于点O,平分 , 若 , 则 的度数为 . 14. 如图,直线a、b被直线c所截,则与是内错角.
14. 如图,直线a、b被直线c所截,则与是内错角. 15. 如图,直线a,b被直线c所截, 的同旁内角是 .
15. 如图,直线a,b被直线c所截, 的同旁内角是 .
三、解答题
-
16. 如图,和相交于点 , 平分 , 于点 , , 求的度数.
 17. 如图,直线AB,CD相交于点O,OF⊥OC于O,OE平分∠AOF,∠COE=15°,求∠BOD的度数.
17. 如图,直线AB,CD相交于点O,OF⊥OC于O,OE平分∠AOF,∠COE=15°,求∠BOD的度数. 18. 如图,指出图中直线AC , BC被直线AB所截的同位角、内错角、同旁内角.
18. 如图,指出图中直线AC , BC被直线AB所截的同位角、内错角、同旁内角.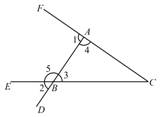
四、综合题
-
19. 如图,已知直线AB,CD相交于点O,∠COE=90°.
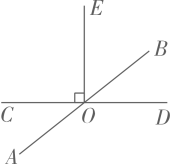 (1)、写出∠BOD的对顶角和余角(2)、若∠AOC=35°,求∠BOE的度数.20. 已知:如图,直线相交于点O,平分 , .
(1)、写出∠BOD的对顶角和余角(2)、若∠AOC=35°,求∠BOE的度数.20. 已知:如图,直线相交于点O,平分 , . (1)、的对顶角是;的邻补角是 .(2)、求的度数.
(1)、的对顶角是;的邻补角是 .(2)、求的度数.

