【浙江衢州】备战2023年中考数学真题变式题第23-24题
试卷更新日期:2023-05-11 类型:三轮冲刺
一、原题23
-
1. 如图1为北京冬奥会“雪飞天”滑雪大跳台赛道的横截面示意图.取水平线OE为x轴,铅垂线OD为y轴,建立平面直角坐标系.运动员以速度从D点滑出,运动轨迹近似抛物线 . 某运动员7次试跳的轨迹如图2.在着陆坡CE上设置点K(与DO相距32m)作为标准点,着陆点在K点或超过K点视为成绩达标.
(参考数据: , )
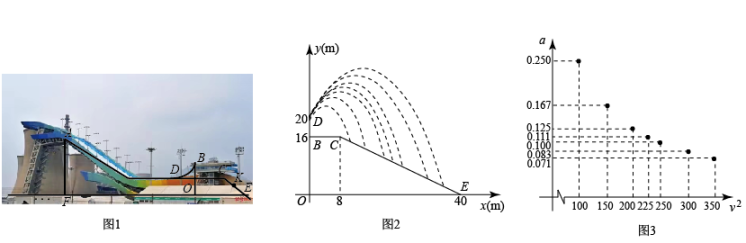 (1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.
(1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.①猜想a关于的函数类型,求函数表达式,并任选一对对应值验证.
②当v为多少m/s时,运动员的成绩恰能达标(精确到1m/s)?
二、变式题1基础
-
2. 已知二次函数y=x2﹣mx+2m﹣4
证明:无论m取任何实数时,该函数图象与x轴总有交点
3. 求抛物线y=x2﹣x+1在﹣2≤x≤2的最大值与最小值.4. 已知抛物线 (a,c为常数, )经过点 ,顶点为D.(Ⅰ)当 时,求该抛物线的顶点坐标;
(Ⅱ)当 时,点 ,若 ,求该抛物线的解析式;
(Ⅲ)当 时,点 ,过点C作直线l平行于x轴, 是x轴上的动点, 是直线l上的动点.当a为何值时, 的最小值为 ,并求此时点M,N的坐标.
三、变式题2巩固
-
5. 如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A、B、C、D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=(x-1)2-4,AB为半圆的直径,求这个“果圆”被y轴截得的CD的长.
 6. 已知抛物线y=x2﹣bx+c(b , c为常数,b>0)经过点A(﹣1,0),点M(m , 0)是x轴正半轴上的动点.
6. 已知抛物线y=x2﹣bx+c(b , c为常数,b>0)经过点A(﹣1,0),点M(m , 0)是x轴正半轴上的动点.(Ⅰ)当b=2时,求抛物线的顶点坐标;
(Ⅱ)点D(b , yD)在抛物线上,当AM=AD , m=5时,求b的值;
(Ⅲ)点Q(b+ ,yQ)在抛物线上,当 AM+2QM的最小值为 时,求b的值.
四、变式题3提升
-
7. 如图,抛物线 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为 .

①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
8. 如图,B(2m , 0)、C(3m , 0)是平面直角坐标系中两点,其中m为常数,且m>0,E(0,n)为y轴上一动点,以BC为边在x轴上方作矩形ABCD , 使AB=2BC , 画射线OA , 把△ADC绕点C逆时针旋转90°得△A′D′C′,连接ED′,抛物线y=ax2+bx+n(a≠0)过E、A′两点.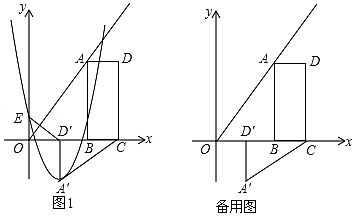 (1)、填空:∠AOB=°,用m表示点A′的坐标:A′;(2)、当抛物线的顶点为A′,抛物线与线段AB交于点P , 且 时,△D′OE与△ABC是否相似?说明理由;(3)、若E与原点O重合,抛物线与射线OA的另一个交点为M , 过M作MN垂直y轴,垂足为N:
(1)、填空:∠AOB=°,用m表示点A′的坐标:A′;(2)、当抛物线的顶点为A′,抛物线与线段AB交于点P , 且 时,△D′OE与△ABC是否相似?说明理由;(3)、若E与原点O重合,抛物线与射线OA的另一个交点为M , 过M作MN垂直y轴,垂足为N:①求a、
B、m满足的关系式;
②当m为定值,抛物线与四边形ABCD有公共点,线段MN的最大值为5,请你探究a的取值范围.
五、原题24
-
9. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G.
 (1)、求证:.(2)、若 .
(1)、求证:.(2)、若 .①求菱形的面积.
②求的值.
(3)、若 , 当的大小发生变化时(),在AE上找一点T,使GT为定值,说明理由并求出ET的值.六、变式题4基础
-
10. 如图,四边形ABCD是菱形,E,F是对角线AC上的两点,且 ,连接BF.FD,DE,EB.
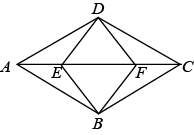
求证:四边形DEBF是菱形.
11. 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交CE的延长线于点F.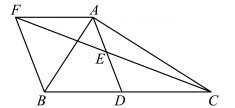 (1)、求证:四边形ADBF是菱形;(2)、若AB=8,菱形ADBF的面积为40,求AC的长.12. 如图,在菱形ABCD中,点E,F分别在边AB,BC上,BE=BF,DE,DF分别与AC交于点M,N.
(1)、求证:四边形ADBF是菱形;(2)、若AB=8,菱形ADBF的面积为40,求AC的长.12. 如图,在菱形ABCD中,点E,F分别在边AB,BC上,BE=BF,DE,DF分别与AC交于点M,N.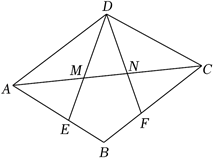
求证:
(1)、△ADE≌△CDF.(2)、ME=NF.13. 在四边形ABCD中,对角线AC、BD交于点O.若四边形ABCD是正方形如图1:则有AC=BD,AC⊥BD.旋转图1中的Rt△COD到图2所示的位置,AC′与BD′有什么关系?(直接写出)
若四边形ABCD是菱形,∠ABC=60°,旋转Rt△COD至图3所示的位置,AC′与BD′又有什么关系?写出结论并证明.


七、变式题5巩固
-
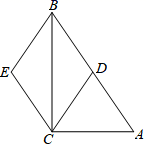
14. 如图,在 中, , 为 边上的中线,过点 作 ,过点 作 , 与 相交于点 .求证:四边形 为菱形.
 15. 如图,四边形中,ABDC, , 于点 .
15. 如图,四边形中,ABDC, , 于点 .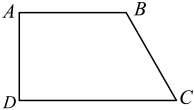 (1)、用尺规作的角平分线,交于点;(不写作法,保留作图痕迹)(2)、连接 . 求证:四边形是菱形.16. 已知:如图,在菱形ABCD中,点E、F分别在边AB、AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.
(1)、用尺规作的角平分线,交于点;(不写作法,保留作图痕迹)(2)、连接 . 求证:四边形是菱形.16. 已知:如图,在菱形ABCD中,点E、F分别在边AB、AD上,BE=DF,CE的延长线交DA的延长线于点G,CF的延长线交BA的延长线于点H.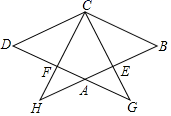 (1)、求证:△BEC∽△BCH;(2)、如果BE2=AB•AE,求证:AG=DF.17. 如图,在菱形ABCD中,连结BD、AC交于点O,过点O作 于点H,以点O为圆心,OH为半径的半圆交AC于点M.
(1)、求证:△BEC∽△BCH;(2)、如果BE2=AB•AE,求证:AG=DF.17. 如图,在菱形ABCD中,连结BD、AC交于点O,过点O作 于点H,以点O为圆心,OH为半径的半圆交AC于点M.
①求证:DC是⊙O的切线.
②若 且 ,求图中阴影部分的面积.
③在②的条件下,P是线段BD上的一动点,当PD为何值时, 的值最小,并求出最小值.
18. 如图,以为边分别作菱形和菱形(点 , , 共线),动点在以为直径且处于菱形内的圆弧上,连接交于点.设.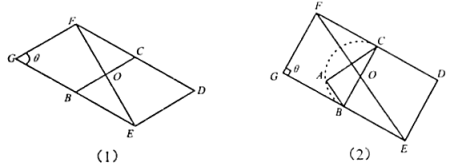 (1)、求证:无论为何值,与相互平分;并请直接写出使成立的值.(2)、当时,试给出的值,使得垂直平分 , 请说明理由.
(1)、求证:无论为何值,与相互平分;并请直接写出使成立的值.(2)、当时,试给出的值,使得垂直平分 , 请说明理由.八、变式题6提升
-
19. 在数学兴趣小组活动中,同学们对菱形的折叠问题进行了探究.如图(1),在菱形中,为锐角,为中点,连接 , 将菱形沿折叠,得到四边形 , 点的对应点为点 , 点的对应点为点.
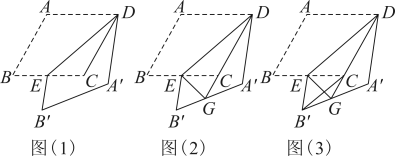 (1)、【观察发现】与的位置关系是;(2)、【思考表达】连接 , 判断与是否相等,并说明理由;(3)、如图(2),延长交于点 , 连接 , 请探究的度数,并说明理由;(4)、【综合运用】如图(3),当时,连接 , 延长交于点 , 连接 , 请写出、、之间的数量关系,并说明理由.20. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .
(1)、【观察发现】与的位置关系是;(2)、【思考表达】连接 , 判断与是否相等,并说明理由;(3)、如图(2),延长交于点 , 连接 , 请探究的度数,并说明理由;(4)、【综合运用】如图(3),当时,连接 , 延长交于点 , 连接 , 请写出、、之间的数量关系,并说明理由.20. 如图1,在矩形中, , , 是边上的一点,连接 , 将矩形沿折叠,顶点恰好落在边上的点处,延长交的延长线于点 .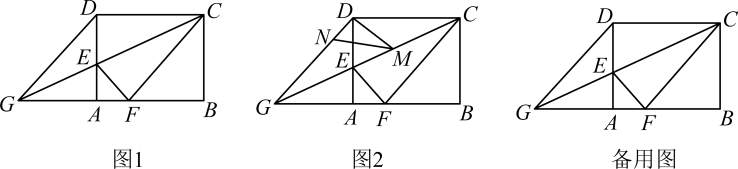 (1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.
(1)、求线段的长;(2)、求证四边形为菱形;(3)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 , 设 , 是否存在这样的点 , 使是直角三角形?若存在,请求出的值;若不存在,请说明理由.
-
-