【浙江衢州】备战2023年中考数学真题变式题第17-18题
试卷更新日期:2023-05-11 类型:三轮冲刺
一、原题17
-
1.(1)、因式分解: .(2)、化简: .
二、变式题1基础
-
2. 因式分解:(1)、;(2)、.3. 因式分解: .4. 因式分解下列各题:(1)、(2)、5. 化简: ﹣ .6. 计算: .
三、变式题2巩固
-
7.(1)、运用乘法公式计算:;(2)、分解因式:.8. 请将下列各式因式分解.(1)、3a(x﹣y)﹣5b(y﹣x);(2)、x2(a﹣b)2﹣y2(b﹣a)2 .(3)、2xmyn﹣1﹣4xm﹣1yn(m,n均为大于1的整数).
四、变式题3提升
-
9. 某学生化简分式 + 出现了错误,解答过程如下:
原式= + (第一步)
= (第二步)
= .(第三步)
(1)、该学生解答过程是从第步开始出错的,其错误原因是;(2)、请写出此题正确的解答过程.五、原题18
-
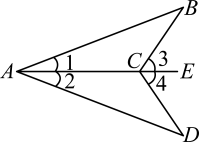
10. 已知:如图, . 求证: .
六、变式题4基础
-
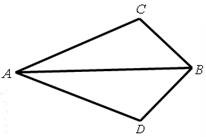
11. 如图,AB平分∠CAD,AC=AD.求证:BC=BD.
 12. 如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE,求证:AB=CD.
12. 如图,点C在线段BD上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE,求证:AB=CD.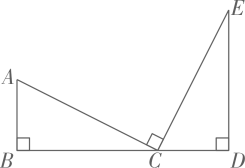 13. 如图,在 中, ,点E在 的延长线上, 于点D,若 ,求证: .
13. 如图,在 中, ,点E在 的延长线上, 于点D,若 ,求证: .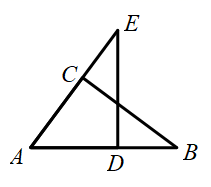
七、变式题5巩固
-
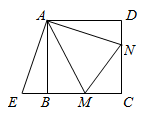
14. 如图,在正方形 中,点E在 边的延长线上,点F在 边的延长线上,且 ,连接 和 相交于点M.
求证: .
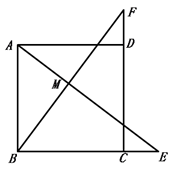 15. 在①AD=AE,②∠ABE=∠ACD,③FB=FC 这三个条件中选择其中一个 , 补充在下面的问题中,并完成问题的解答。
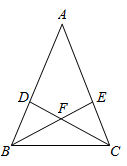
15. 在①AD=AE,②∠ABE=∠ACD,③FB=FC 这三个条件中选择其中一个 , 补充在下面的问题中,并完成问题的解答。问题:如图,在△ABC中,∠ABC=∠ACB,点D在AB边上(不与点A,点B重合),点E在AC边上(不与点A,点C重合),连结BE,CD,BE与CD相交于点F。若_▲_,求证:BE=CD 。
注:如果选择多个条件分别作答,按第一个解答计分。
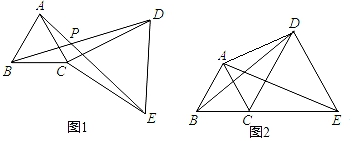
16. 如图, , , .求证: .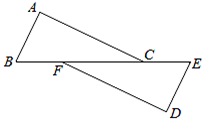 17. 如图,已知AB=AC,AD=AE,BD和CE相交于点O.
17. 如图,已知AB=AC,AD=AE,BD和CE相交于点O.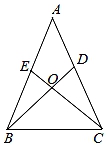 (1)、求证:△ABD≌△ACE;(2)、判断△BOC的形状,并说明理由.18. 如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE。
(1)、求证:△ABD≌△ACE;(2)、判断△BOC的形状,并说明理由.18. 如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE。 (1)、求证:△ABC≌△DCE(2)、连结AE,当BC=5,AC=12时,求AE的长。
(1)、求证:△ABC≌△DCE(2)、连结AE,当BC=5,AC=12时,求AE的长。八、变式题6提升
-
-
-