【浙江衢州】备战2023年中考数学真题变式题第15-16题-在线组卷题库

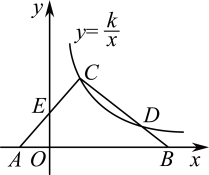
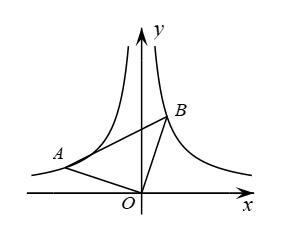
1. 如图，在△ABC中，边AB在x轴上，边AC交y轴于点E．反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象恰好经过点C，与边BC交于点D．若AE=CE，CD=2BD， $S_{△ A B C} = 6$ ，则k= ．

查看试题解析

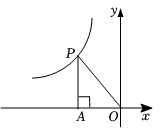
2. 如图，点P（x，y）在双曲线 $y = \frac{k}{x}$ 的图象上，PA⊥x轴，垂足为A，若S_△AOP＝2，则该反比例函数的解析式为 .

查看试题解析
3. 平面直角坐标系 $x O y$ 中，已知点 $A (m ， 6 m) ， B (3 m ， 2 n) ， C (- 3 m ， - 2 n)$ 是函数 $y = \frac{k}{x} (k \neq 0)$ 图象上的三点。若 $S_{△ A B C} = 2$ ，则k的值为．

查看试题解析
4. 如图，在平面直角坐标系中， $O$ 是坐标原点．在 $R t △ O A B$ 中， $∠ O A B = 90 °$ ，边 $O A$ 在 $y$ 轴上，点 $D$ 是边 $O B$ 上一点，且 $O D ： D B = 1 ： 2$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象经过点 $D$ 交 $A B$ 于点 $C$ ，连接 $O C$ ．若 $S_{△ O B C} = 4$ ，则 $k$ 的值为．

查看试题解析

5. 如图，在平面直角坐标系中，Rt $△ O A B$ 的直角顶点B在x轴的正半轴上，点O与原点重合，点A在第一象限，反比例函数 $y = \frac{k}{x}$ （ $x > 0$ ）的图象经过OA的中点C，交 $A B$ 于点D，连接 $C D$ ．若 $△ A C D$ 的面积是1，则k的值是．

查看试题解析
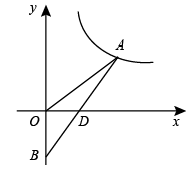
6. 如图，在平面直角坐标系中，△AOB的边OB在y轴上，边AB与x轴交于点D，且BD=AD，反比例函数y= $\frac{k}{x}$ (x>0)的图象经过点A，若S_△OAB=1，则k的值为．

查看试题解析
7. 正方形ABCD在平面直角坐标系中的位置如图所示，点A的坐标为（2，0），点B的坐标为（0，4）．若反比例函数y＝ $\frac{k}{x}$ （k≠0）的图象经过点C，则k的值为．

查看试题解析
8. 如图，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过 $▱ A B C D$ 对角线的交点P，已知点A，C，D在坐标轴上， $B D ⊥ D C$ ， $▱ A B C D$ 的面积为8，则 $k =$ ．

查看试题解析

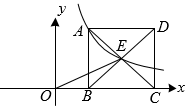
9. 如图，反比例函数 $y = \frac{k}{x}$ 的图象经过矩形 $A B C D$ 对角线的交点E和点A，点B、C在x轴上， $△ O C E$ 的面积为6，则 $k =$ ．

查看试题解析
10. 如图， $△ O A B$ 是等腰直角三角形，直角顶点与坐标原点重合，若点B在反比例函数 $y = \frac{1}{x} (x > 0)$ 的图象上，则经过点A的反比例函数表达式为．

查看试题解析

11. 希腊数学家海伦给出了挖掘直线隧道的方法：如图，A，B是两侧山脚的入口，从B出发任作线段BC，过C作CD⊥BC，然后依次作垂线段DE，EF，FG，GH，直到接近点A，作AJ⊥GH于点J．每条线段可测量，长度如图所示．分别在BC，AJ上任选点M，N，作MQ⊥BC，NP⊥AJ，使得 $\frac{P N}{A N} = \frac{Q M}{B M} = k$ ，此时点P，A，B，Q共线．挖隧道时始终能看见P，Q处的标志即可．

(1)、 $C D - E F - G J =$ km．

(2)、 $k$ = ．

查看试题解析

12. 如图1是某激光黑白A4纸张打印机的机身，其侧面示意图如图2， $A B ⊥ B C$ ， $C D ⊥ B C$ .出纸盘 $E P$ 下方为一段以 $O$ 为圆心的圆弧 $\overset{⌢}{D E}$ ，与上部面板线段 $A E$ 相接于点 $E$ ，与 $C D$ 相切于点 $D$ .测得 $B C = 24 cm$ ， $C D = 18 cm$ .进纸盘 $C H$ 可以随调节扣 $H F$ 向右平移， $C H = 18 cm$ ， $H F = 2 cm$ .当 $H F$ 向右移动 $6 cm$ 至 $H F$ 时，点 $A$ ， $D$ ， $F$ 在同一直线上，则 $A B$ 的长度为 $cm$ .若点 $E$ 到 $A B$ 的距离为 $16 cm$ ， $\tan A = 4$ ，连结 $P O$ ，线段 $O P$ 恰好过 $\overset{⌢}{D E}$ 的中点.若 $P E = 2 \sqrt{65} cm$ ，则点 $P$ 到直线 $B C$ 的距离为 $cm$ .

查看试题解析
13. 《九章算术》是中国传统数学最重要的著作，在“勾股”章中有这样一个问题：“今有邑方二百步，各中开门，出东门十五步有木，问：出南门几步而见木？”
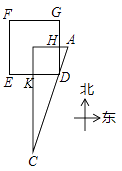
用今天的话说，大意是：如图， $D E F G$ 是一座边长为200步（“步”是古代的长度单位）的正方形小城，东门 $H$ 位于 $G D$ 的中点，南门 $K$ 位于 $E D$ 的中点，出东门15步的 $A$ 处有一树木，求出南门多少步恰好看到位于 $A$ 处的树木（即点 $D$ 在直线 $A C$ 上）？请你计算 $K C$ 的长为步．

查看试题解析
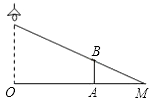
14. 如图，路灯距离地面8米，身高1.6米的小明站在距离灯的底部（点O）20米的A处，则小明的影子AM长为米．

查看试题解析
15. “今有邑，东西七里，南北九里，各开中门，出东门一十五里有木，问：出南门几何步而见木？”这段话摘自《九章算术》，意思是说：如图，矩形城池ABCD，东边城墙AB长9里，南边城墙AD长7里，东门点E、南门点F分别是AB，AD的中点，EG⊥AB，FH⊥AD，EG=15里，HG经过A点，则FH=里．

查看试题解析
16.
如图，在平面直角坐标系xOy中，直线y=-x+m分别交于x轴、y轴于A，B两点，已知点C（2，0）.

(1)、当直线AB经过点C时，点O到直线AB的距离是；

(2)、设点P为线段OB的中点，连结PA，PC，若∠CPA=∠ABO，则m的值是.

查看试题解析

17. 如图1是一种利用镜面反射，放大微小变化的装置.木条BC上的点P处安装一平面镜，BC与刻度尺边MN的交点为D，从A点发出的光束经平面镜P反射后，在MN上形成一个光点E.已知 $A B ⊥ B C ， M N ⊥ B C ， A B = 6.5$ ， $B P = 4 ， P D = 8$ .

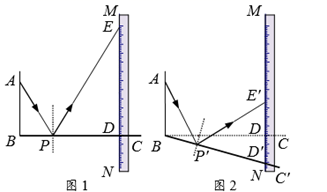(1)、ED的长为.

(2)、将木条BC绕点B按顺时针方向旋转一定角度得到 $B C^{'}$ （如图2），点P的对应点为 $P^{'}$ ， $B C^{'}$ 与MN的交点为D′，从A点发出的光束经平面镜 $P^{'}$ 反射后，在MN上的光点为 $E^{'}$ .若 $D D^{'} = 5$ ，则 $E E^{'}$ 的长为.

查看试题解析
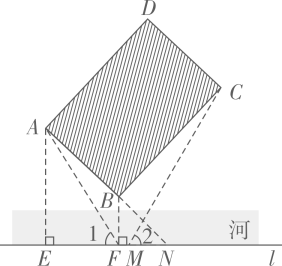
18. 如图，在河对岸有一矩形场地ABCD，为了估测场地大小，在笔直的河岸l上依次取点E，F，N，使AE⊥l，BF⊥l，点N，A，B在同一直线上。在F点观测A点后，沿FN方向走到M点.观测C点发现∠1=∠2。测得EF=15米，FM=2米，MN=8米，∠ANE=45°，则场地的边AB为米，BC为米。

查看试题解析
19.
如图，边长为4的正方形ABCD中，P是BC边上一动点（不含B、C点）．将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．则以下结论中正确的有（写出所有正确结论的序号）．
①∠NAP=45°；
②当P为BC中点时，AE为线段NP的中垂线；
③四边形AMCB的面积最大值为10；
④线段AM的最小值为2 $\sqrt{5}$ ；
⑤当△ABP≌△ADN时，BP=4 $\sqrt{2}$ ﹣4．

查看试题解析

20. 图1是某折叠式靠背椅实物图，图2是椅子打开时的侧面示意图，椅面CE与地面平行，支撑杆AD，BC可绕连接点O转动，且 $O A = O B$ ，椅面底部有一根可以绕点H转动的连杆HD，点H是CD的中点，FA，EB均与地面垂直，测得 $F A = 54 cm$ ， $E B = 45 cm$ ， $A B = 48 cm$ .

(1)、椅面CE的长度为cm.

(2)、如图3，椅子折叠时，连杆HD绕着支点H带动支撑杆AD，BC转动合拢，椅面和连杆夹角 $∠ C H D$ 的度数达到最小值 $30 °$ 时，A，B两点间的距离为cm（结果精确到0.1cm）.（参考数据： $\sin 15 ° \approx 0.26$ ， $\cos 15 ° \approx 0.97$ ， $\tan 15 ° \approx 0.27$ ）

查看试题解析

【浙江衢州】备战2023年中考数学真题变式题第15-16题

一、原题15

二、变式题1基础

三、变式题2巩固

四、变式题3提升

五、原题16

六、变式题4基础

七、变式题5巩固

八、变式题6提升