【浙江衢州】备战2023年中考数学真题变式题第13-14题
试卷更新日期:2023-05-11 类型:三轮冲刺
一、原题13
-
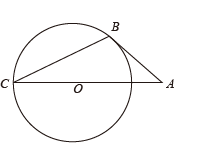
1. 如图,AB切⊙O于点 , AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C的度数为 .
二、变式题1基础
-
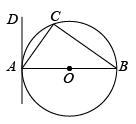
2. 如图,内接于是直径,过点A作的切线 . 若 , 则的度数是度.
 3. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.
3. 如图,、是的弦,过点A的切线交的延长线于点 , 若 , 则°.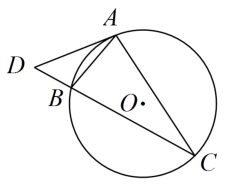 4. 如图,AB是 的直径,PA切 于点A , 线段PO交 于点C . 连接BC , 若 ,则 .
4. 如图,AB是 的直径,PA切 于点A , 线段PO交 于点C . 连接BC , 若 ,则 .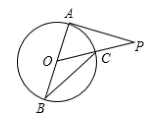
三、变式题2巩固
-
5. 如图,已知 是 的直径, 是 的切线,连接 交 于点D,连接 .若 ,则 的度数是 .
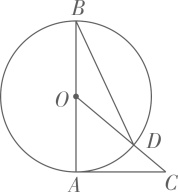 6. 如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到 ,使点 落在 上,边 交线段 于点 .若 ,则 度.
6. 如图, 与 的边 相切,切点为 .将 绕点 按顺时针方向旋转得到 ,使点 落在 上,边 交线段 于点 .若 ,则 度.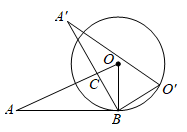 7. 如图, 是 的切线, 是切点.若 ,则 .
7. 如图, 是 的切线, 是切点.若 ,则 .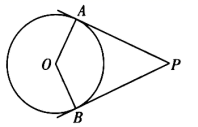 8. 如图,正六边形 ABCDEF 内接于⊙O.若直线 PA 与⊙O 相切于点 A,则∠PAB=.
8. 如图,正六边形 ABCDEF 内接于⊙O.若直线 PA 与⊙O 相切于点 A,则∠PAB=.
四、变式题3提升
-
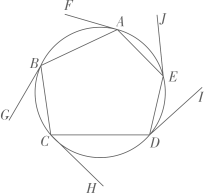
9. 如图, 是五边形 的外接圆的切线,则 .
五、原题14
-
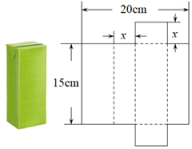
10. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).
六、变式题4基础
-
11. 为创建“国家生态园林城市”,某小区在规划设计时,在小区中央设置一块面积为1200平方米的矩形绿地,并且长比宽多40米.设绿地宽为x米,根据题意,可列方程为 .
12. 如图,要在一块长20米、宽15米的矩形地面上,修建了三条宽度相等的道路(其中两条路与宽平行,一条路与长平行).若要使剩余部分的面积为208平方米,则道路的宽为米.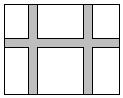 13. 中国古代数学家杨辉的《田亩比数乘除减法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步,问它的长与宽各多少步?利用方程思想,设宽为x步,则依题意列方程为 .14. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.
13. 中国古代数学家杨辉的《田亩比数乘除减法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步,问它的长与宽各多少步?利用方程思想,设宽为x步,则依题意列方程为 .14. 列方程(组)解应用题:某驻村工作队,为带动群众增收致富,巩固脱贫攻坚成效,决定在该村山脚下,围一块面积为600m2的矩形试验茶园,便于成功后大面积推广.如图所示,茶园一面靠墙,墙长35m,另外三面用69m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).求这个茶园的长和宽.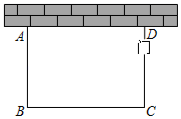 15. 如图,有一块矩形硬纸板,长 ,宽 .在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为 ?
15. 如图,有一块矩形硬纸板,长 ,宽 .在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为 ?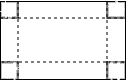
七、变式题5巩固
-
16. 1275年,我国南宋数学家杨辉在《田亩比类乘除算法》中提出这样一个问题:直田积八百六十四步,只云阔不及长一十二步.问阔及长各几步.意思是:矩形面积864平方步,宽比长少12步,问宽和长各几步.若设长为x步,则可列方程为.17. 某校劳动教育课上,老师让同学们设计劳动基地的规划.如图,在块长、宽的矩形空地上,修建两条同样宽的相互垂直的道路,剩余部分栽种绿植,要使栽种面积为 , 则修建的路宽应为多少米?
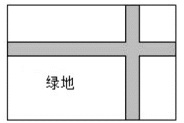 18. 改善小区环境,争创文明家园.如图所示,某社区决定在一块长( )16 ,宽( )9 的矩形场地 上修建三条同样宽的小路,其中两条与 平行,另一条与 平行,其余部分种草.要使草坪部分的总面积为112 ,则小路的宽应为多少?
18. 改善小区环境,争创文明家园.如图所示,某社区决定在一块长( )16 ,宽( )9 的矩形场地 上修建三条同样宽的小路,其中两条与 平行,另一条与 平行,其余部分种草.要使草坪部分的总面积为112 ,则小路的宽应为多少? 19. 某地计划对矩形广场进行扩建改造.如图,原广场长50m,宽40m,要求扩充后的矩形广场长与宽的比为3:2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米100元.如果计划总费用642000元,扩充后广场的长和宽应分别是多少米?
19. 某地计划对矩形广场进行扩建改造.如图,原广场长50m,宽40m,要求扩充后的矩形广场长与宽的比为3:2.扩充区域的扩建费用每平方米30元,扩建后在原广场和扩充区域都铺设地砖,铺设地砖费用每平方米100元.如果计划总费用642000元,扩充后广场的长和宽应分别是多少米?
八、变式题6提升
-
20. 如图,在矩形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,当点Q运动到点C时,两点停止运动,设运动时间为t秒.
 (1)、填空:BQ=cm,PB=cm;(用含t的代数式表示)(2)、当t为何值时,PQ的长度等于5cm?(3)、是否存在t的值,使得五边形APQCD的面积等于26cm2?若存在,请求出此时t的值;若不存在,请说明理由.
(1)、填空:BQ=cm,PB=cm;(用含t的代数式表示)(2)、当t为何值时,PQ的长度等于5cm?(3)、是否存在t的值,使得五边形APQCD的面积等于26cm2?若存在,请求出此时t的值;若不存在,请说明理由.
-
-
-