【浙江衢州】备战2023年中考数学真题变式题第7-8题
试卷更新日期:2023-05-11 类型:三轮冲刺
一、原题7
-
1. 不等式组 , 的解集是( )A、 B、无解 C、 D、
二、变式题1基础
-
2. 若x=2是下列四个选项中的某个不等式组的一个解,则这个不等式组是( )A、 B、 C、 D、3. 不等式组的解集在数轴上表示正确的是( )A、
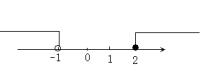 B、
B、 C、
C、 D、
D、
三、变式题2巩固
-
4. 若关于x的不等式组仅有3个整数解,则a的取值范围是( )A、-4≤a<-2 B、-3<a≤-2 C、-3≤a≤-2 D、-3≤a<-25. 如果点P(m,1+2m)在第三象限内,那么m的取值范围是( )A、 B、 C、 D、6. 若关于x的不等式组 恰有3个整数解,则实数a的取值范围是( )A、 B、 C、 D、7. 不等式1<2x-3<x+1的解集是( )A、1<x<2 B、2<x<3 C、2<x<4 D、4<x<5
四、变式题3提升
-
8. 关于x的分式方程 的解为正数,且关于y的不等式组 的解集为y≥5,则所有满足条件的整数a的值之和是( )A、13 B、15 C、18 D、209. 定义一种运算: ,则不等式 的解集是( )A、 或 B、 C、 或 D、 或
五、原题8
-
10. 西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位置,从矩的一端A(人眼)望点E,使视线通过点C,记人站立的位置为点B,量出BG长,即可算得物高EG.令BG=x(m), EG=y(m),若a=30cm,b=60cm,AB=1.6m,则y关于x的函数表达式为( )
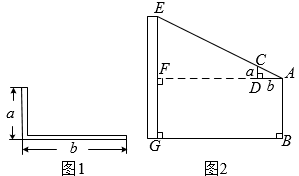 A、 B、 C、 D、
A、 B、 C、 D、六、变式题4基础
-
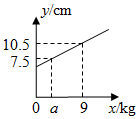
11. 如图,一个弹簧不挂重物时长6cm,挂上重物后,在弹性限度内弹簧伸长的长度与所挂重物的质量成正比.弹簧总长y(单位:cm)关于所挂物体质量x(单位:kg)的函数图象如图所示,则图中a的值是( )
 A、3 B、4 C、5 D、612. 已知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( )A、y=4x(x≥0) B、y=4x-3(x≥ ) C、y=3-4x(x≥0) D、y=3-4x(0≤x≤ )13. 小涵与阿嘉一起去咖啡店购买同款咖啡豆,咖啡豆每公克的价钱固定,购买时自备容器则结帐金额再减5元.若小涵购买咖啡豆250公克且自备容器,需支付295元;阿嘉购买咖啡豆x公克但没有自备容器,需支付y元,则y与x的关系式为下列何者?( )
A、3 B、4 C、5 D、612. 已知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/小时,若用x表示行走的时间(小时),y表示余下的路程(千米),则y关于x的函数解析式是( )A、y=4x(x≥0) B、y=4x-3(x≥ ) C、y=3-4x(x≥0) D、y=3-4x(0≤x≤ )13. 小涵与阿嘉一起去咖啡店购买同款咖啡豆,咖啡豆每公克的价钱固定,购买时自备容器则结帐金额再减5元.若小涵购买咖啡豆250公克且自备容器,需支付295元;阿嘉购买咖啡豆x公克但没有自备容器,需支付y元,则y与x的关系式为下列何者?( )
A、 B、 C、 D、14. 长方形的周长为24 cm,其中一边长为x cm(其中0<x<12),面积为y cm2 , 则该长方形中y与x的关系式可以写为( )A、y=x2 B、y=(12-x)2 C、y=(12-x)·x D、y=2(12-x)15. 某校组织学生到距学校6 km的光明科技馆参观.王红准备乘出租车去科技馆,出租车的收费标准如下表:里程数
收费/元
3 km以下(含3 km)
8.00
3 km以上每增加1 km
1.80
则收费y(元)与出租车行驶里程数x(km)(x≥3)之间的关系式为( )
A、y=8x B、y=1.8x C、y=8+1.8x D、y=2.6+1.8x16. 表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )甲方案
乙方案
门号的月租费(元)
400
600
MAT手机价格(元)
15000
13000
注意事项:以上方案两年内不可变更月租费
A、500 B、516 C、517 D、600七、变式题5巩固
-
17. 小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )
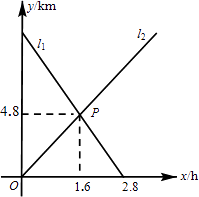 A、3km/h和4km/h B、3km/h和3km/h C、4km/h和4km/h D、4km/h和3km/h18. 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
A、3km/h和4km/h B、3km/h和3km/h C、4km/h和4km/h D、4km/h和3km/h18. 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个八、变式题6提升
-
19. 小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:

①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )
A、1个 B、2个 C、3个 D、4个20. 甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:①A,B之间的距离为1200m;
②乙行走的速度是甲的1.5倍;
③b=960;
④a=34.
以上结论正确的有( )
 A、①② B、①②③ C、①③④ D、①②④
A、①② B、①②③ C、①③④ D、①②④
-
-