人教版七年级下数学期末复习知识点扫盲满分计划——7.1平面直角坐标系
试卷更新日期:2023-05-11 类型:复习试卷
一、写出直角坐标系中点坐标
-
1. 已知平面直角坐标系中有一点M(m-1,2m+3).若点M在x轴上,求M的坐标2. 在平面直角坐标系中,已知点P的坐标为(1)、若点P在y轴上,求点P的坐标;(2)、若点P在第四象限,求a的取值范围.3. 已知线段AB∥y轴,点A(1,-3),B(m,n),且AB=5时,点B的坐标为 .4. 在平面直角坐标系中,已知点 , 点P在过点,且与x轴平行的直线上,求出点P的坐标.5. 平面直角坐标系中,点 , , 经过点A的直线a与x轴平行,如果点C是直线a上的一个动点,那么当线段的长度最短时,点C的坐标为( )A、 B、 C、 D、
二、求点到坐标轴的距离
-
6. 点到x轴距离为 , 到y轴距离为 .7. 点到y轴距离为 .8. 在平面直角坐标系中,点P的坐标是(3,﹣4),则点P到x轴的距离为 .9. 点A(-3,-2)到y轴的距离为( )A、-3个单位长度 B、-2个单位长度 C、2个单位长度 D、3个单位长度10. 平面直角坐标系中,点到x轴的距离是 .
三、判断点所在的象限
-
11. 在平面直角坐标系中,点A的坐标是(3a﹣9,a﹣2),则下列说法正确的是( )A、当点A在x轴上时,a=3 B、当点A在y轴上时,a=2 C、当a>3时,点A在第一象限 D、当a<2时,点A在第二象限12. 已知点在轴的负半轴上,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限13. 在平面直角坐标系中,点P( , )一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限14. 下列命题:①方程 有无数组整数解﹔②垂直于同一直线的两条直线互相平行﹔③若 是关于 的一元一次不等式,则 ;④若 ,则点 在第二、四象限.其中是真命题的个数是( )A、1个 B、2个 C、3个 D、4个15. 在平面直角坐标系中,点 在( ).A、 轴正半轴上 B、 轴负半轴上 C、 轴正半轴上 D、 轴负半轴上
四、已知点所在的象限求参数
-
16. 已知点在第一象限,且到两坐标轴距离相等,则的值是 .17.(1)、平面直角坐标系中,有一点 , 当点到轴距离是1时,求的值.(2)、已知 , .
已知的算术平方根为3,求的值;
如果一个正数的平方根分别为、 , 求这个正数.
18. 平面直角坐标系上有一点 , 请根据题意回答下列问题:(1)、若点P在x轴上,求出点P的坐标.(2)、点Q的坐标为且轴,求出点P的坐标.(3)、若点P到y轴的距离为2,直接写出a的值.19. 在平面直角坐标系中,已知点 .(1)、将点M向下平移1个单位长度得到 , 则k的值为(2)、已知点M在第二象限,若点M到y轴的距离是它到x轴距离的2倍,则k的值为20. 若点A(3,a+1)在x轴上,点B(2b﹣1,1)在y轴上,则a﹣b的值为( )A、 B、 C、 D、五、坐标与图形
-
21. 在平面直角坐标系中,点O为坐标原点,点的坐标分别为 , , , 若的面积为面积的2倍,则m的值为22. 如图,已知在平面直角坐标系中, , , 三角形的面积为24,点P是x轴的上方距离x轴的距离为6的直线上的任意一点.
 (1)、A点的坐标为 , C的坐标为;(2)、若点P的横坐标为1,连接 , , 则三角形的面积为;(3)、是否存在点P,使三角形的面积等于的面积?如果存在,请求出点P的坐标;若不存在,请说明理由.23. 如图所示,在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是 , , , 先将向上平移3个单位长度,再向右平移2个单位长度,得到 .
(1)、A点的坐标为 , C的坐标为;(2)、若点P的横坐标为1,连接 , , 则三角形的面积为;(3)、是否存在点P,使三角形的面积等于的面积?如果存在,请求出点P的坐标;若不存在,请说明理由.23. 如图所示,在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是 , , , 先将向上平移3个单位长度,再向右平移2个单位长度,得到 .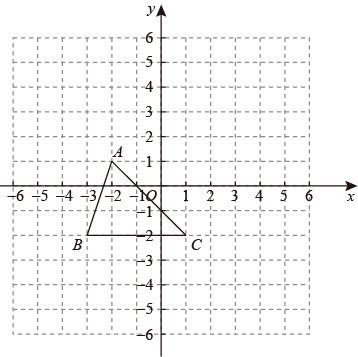 (1)、在图中画出 .(2)、写出点的坐标.(3)、若y轴上有一点P,使与面积相等,求出P点的坐标.24. 在平面直角坐标系中,有点A(2,4),点B(0,2),若在坐标轴上有一点C(不与点B重合),使三角形AOC和三角形AOB面积相等,则点C的坐标为 .25. 如图,在平面直角坐标系中,的三个顶点的坐标分别是 , , . 将向上平移4个单位长度,再向右平移5个单位长度,得到 .
(1)、在图中画出 .(2)、写出点的坐标.(3)、若y轴上有一点P,使与面积相等,求出P点的坐标.24. 在平面直角坐标系中,有点A(2,4),点B(0,2),若在坐标轴上有一点C(不与点B重合),使三角形AOC和三角形AOB面积相等,则点C的坐标为 .25. 如图,在平面直角坐标系中,的三个顶点的坐标分别是 , , . 将向上平移4个单位长度,再向右平移5个单位长度,得到 . (1)、直接写出点的坐标;(2)、在平面直角坐标系中画出;(3)、若轴上有一点 , 且的面积与的面积相等,求点的坐标.
(1)、直接写出点的坐标;(2)、在平面直角坐标系中画出;(3)、若轴上有一点 , 且的面积与的面积相等,求点的坐标.六、点坐标规律探索
-
26. 在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右→向下→向右→向上→向右”的方向依次不断运动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点 A1 , 第二次移动到点A2……第n次移动到点An , 则点A2023的坐标是
 27. 在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2 , 点A2的伴随点为A3 , 点A3的伴随点为A4 , …,这样依次得到点A1 , A2 , A3 , …,An , …若点A1的坐标为(2,4),点A2021的坐标为( )A、(3,﹣1) B、(﹣2,﹣2) C、(﹣3,3) D、(2,4 )28. 如图,在平面直角坐标系中, , , , ……根据这个规律,探究可得点的坐标是 .
27. 在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P伴随点.已知点A1的伴随点为A2 , 点A2的伴随点为A3 , 点A3的伴随点为A4 , …,这样依次得到点A1 , A2 , A3 , …,An , …若点A1的坐标为(2,4),点A2021的坐标为( )A、(3,﹣1) B、(﹣2,﹣2) C、(﹣3,3) D、(2,4 )28. 如图,在平面直角坐标系中, , , , ……根据这个规律,探究可得点的坐标是 . 29. 如图,在一个单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7 , ……,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2019的横坐标为( )
29. 如图,在一个单位为1的方格纸上,△A1A2A3 , △A3A4A5 , △A5A6A7 , ……,是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,﹣1),A3(0,0),则依图中所示规律,A2019的横坐标为( ) A、﹣1008 B、2 C、1 D、101130. 如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n是自然数)的坐标为( )
A、﹣1008 B、2 C、1 D、101130. 如图,在平面直角坐标系中,一动点从原点O出发,按向上、向右、向下、向右的方向依次不断地移动,每次移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…,那么点A4n+1(n是自然数)的坐标为( )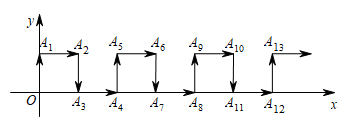 A、(1,2n) B、(2n,1) C、(n,1) D、(2n-1,1)31. 如图,在平面直角坐标系上有点 , 点第一次跳至点 , 第二次向右跳动3个单位至点 , 第三次跳至点 , 第四次向右跳动5个单位至点 , …依此规律跳动下去,点第2022次跳至点的坐标是( )
A、(1,2n) B、(2n,1) C、(n,1) D、(2n-1,1)31. 如图,在平面直角坐标系上有点 , 点第一次跳至点 , 第二次向右跳动3个单位至点 , 第三次跳至点 , 第四次向右跳动5个单位至点 , …依此规律跳动下去,点第2022次跳至点的坐标是( )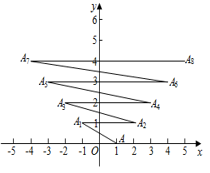 A、 B、 C、 D、
A、 B、 C、 D、七、综合训练
-
32. 已知点在x轴正半轴上,则a的取值范围是 .33. 下列说法错误的是( )A、x轴上的点的纵坐标为0 B、点到y轴的距离是1 C、若点在第二象限,那么 D、若 , 那么点在第四象限34. 平面直角坐标系中.已知轴,M点的坐标为 , 并且MN=4,则N点的坐标为 .35. 已知平面直角坐标系中有一点 .(1)、若点M到x轴的距离为1,请求出点M的坐标.(2)、若点),且轴,求线段的长度.36. 在平面直角坐标系xOy中,点M的坐标是(1,2),轴, , 则点N的坐标是 .37. 已知平面直角坐标系内不同的两点、到x轴的距离相等,则a的值为 .38. 如图所示,在平面直角坐标系中,点A,B的坐标分别为(a,0),B(b,0),且a,b满足 , 点C的坐标为(0,3).
 (1)、求a,b的值及S△ABC;(2)、若点M在x轴上,且 , 试求点M的坐标.39. 在平面直角坐标系中,如果过点A 和B的直线平行于x轴,且AB=4,则点B的坐标为( )A、 B、 C、或 D、或40. 已知点、、 .(1)、若 , 求BC的长;(2)、若点C在x轴上,求三角形ABC的面积.(3)、若点C在y轴上,求证:三角形BOA面积等于三角形BOC面积.41. 在平面直角坐标系xOy中,已知点A(a,﹣1),B(2,3﹣b),C(﹣5,4).若AB∥x轴,AC∥y轴,则a﹣b= .42. 在平面直角坐标系中,以任意两点 P(x1 , y1),Q(x2 , y2)为端点的线段的中点坐标为.现有 A(3,4),B(1,8),C(-2,6)三点,点D为线段AB的中点,点C 为线段AE的中点,则线段DE的中点坐标为.43. 已知,点(1)、若点P的横、纵坐标恰好为一个正数a的两个平方根,则a的值为;(2)、若点到两个坐标轴的距离相等,求点的坐标.44. 已知平面直角坐标系中有一点 .(1)、若点P在第四象限,求m的取值范围;(2)、若点P到y轴的距离为3,且点P在第三象限,求点P的坐标.45. 已知点且 , 则n的值等于 .46. 已知点在y轴上,点在x轴上,则点的坐标为( )A、 B、 C、 D、
(1)、求a,b的值及S△ABC;(2)、若点M在x轴上,且 , 试求点M的坐标.39. 在平面直角坐标系中,如果过点A 和B的直线平行于x轴,且AB=4,则点B的坐标为( )A、 B、 C、或 D、或40. 已知点、、 .(1)、若 , 求BC的长;(2)、若点C在x轴上,求三角形ABC的面积.(3)、若点C在y轴上,求证:三角形BOA面积等于三角形BOC面积.41. 在平面直角坐标系xOy中,已知点A(a,﹣1),B(2,3﹣b),C(﹣5,4).若AB∥x轴,AC∥y轴,则a﹣b= .42. 在平面直角坐标系中,以任意两点 P(x1 , y1),Q(x2 , y2)为端点的线段的中点坐标为.现有 A(3,4),B(1,8),C(-2,6)三点,点D为线段AB的中点,点C 为线段AE的中点,则线段DE的中点坐标为.43. 已知,点(1)、若点P的横、纵坐标恰好为一个正数a的两个平方根,则a的值为;(2)、若点到两个坐标轴的距离相等,求点的坐标.44. 已知平面直角坐标系中有一点 .(1)、若点P在第四象限,求m的取值范围;(2)、若点P到y轴的距离为3,且点P在第三象限,求点P的坐标.45. 已知点且 , 则n的值等于 .46. 已知点在y轴上,点在x轴上,则点的坐标为( )A、 B、 C、 D、