人教版七年级下数学期末复习知识点扫盲满分计划——6.3实数
试卷更新日期:2023-05-11 类型:复习试卷
一、无理数:无限不循环小数
-
1. 在下列各数:3.14,-π, , 、、中无理数的个数是( )A、2 B、3 C、4 D、52. 在 , , , , 这五个数中,无理数的个数为( )A、2 B、3 C、4 D、53. 在下列实数中,无理数是( )A、 B、2 C、 D、4. 在下列实数中:2019, , , 0,π, , (相邻两个3间依次多一个0),其中无理数有个.5. 实数3.141, , π, , , 0.2,0.1010010001……中无理数有个 (填个数).
二、实数的分类:有理数和无理数
-
6. 把下列各数填入相应的括号内:(1)、无理数:{ …};(2)、负实数:{ …};(3)、整 数:{ …};(4)、分 数:{ …};7. 将下列各数进行分类填序号即可:
①1, , ③0,④-3.2, , , 每个“2”之间依次多一个“0“.
正整数: ;
分数: ;
无理数: .
8. 把下列各数填在相应的横线上:0, , , , -3.14, , , 1.212212221……(两个1之间依次多1个2).
整 数:.
负分数:.
无理数:.
9. 将下列各数写到相应的横线上,(填序号)①;②;③;④;⑤;⑥.
(1)、有理数: ;(2)、无理数: ;(3)、负数: .10. 把下列各数填入相应的大括号中:0.3, , , , 0, , 3.14, , , , , 0.125, ,
负数集合{ …};
整数集合{ …};
有理数集合{ …};
无理数集合{ …}.
三、实数与数轴上的点一一对应
-
11. 一只蚂蚁趴在如图所示的数轴上,它从点A沿数轴向右爬行2个单位长度到达点B,设点A表示 , 那么点B所表示的数为( )
 A、 B、 C、 D、12. 在如图所示的数轴上近似地表示下列各数,并用“<”连接.
A、 B、 C、 D、12. 在如图所示的数轴上近似地表示下列各数,并用“<”连接., 1.5, , -π.
 13. 已知实数a在数轴上的位置如图所示,则化简:+的结果为( )
13. 已知实数a在数轴上的位置如图所示,则化简:+的结果为( ) A、2 B、-2 C、2a-6 D、-2a+614. 实数 , 在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A、2 B、-2 C、2a-6 D、-2a+614. 实数 , 在数轴上的对应点的位置如图所示,下列结论中正确的是( ) A、 B、 C、 D、15. 实数a、b在数轴上的位置如图所示,那么化简的结果是( )
A、 B、 C、 D、15. 实数a、b在数轴上的位置如图所示,那么化简的结果是( )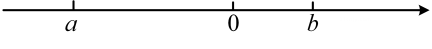 A、 B、b C、 D、
A、 B、b C、 D、四、无理数的整数和小数部分
-
16. 设实数 的整数部分为m,小数部分为n,则(2m+n)(2m-n)的值是( )A、 B、 C、 D、17. 阅读下面材料:.
∵<< , 即2< <3,
∴的整数部分为2,小数部分为-2.
请解答下列问题;
(1)、的整数部分是 , 小数部分是;(2)、已知7-的小数部分是m,7+的小数部分是n,求m+n的值.18. 我们知道,是一个无理数,将这个数减去整数部分,差就是小数部分.即的整数部分是1,小数部分是 , 请回答以下问题:(1)、的小数部分是 , 的小数部分是.(2)、若是的整数部分,是的小数部分.求的平方根.(3)、若 , 其中是整数,且 , 求的值.19. 我们知道≈1.414,于是我们说:“的整数部分为1,小数部分则可记为-1”.则:(1)、+1的整数部分是 , 小数部分可以表示为(2)、已知+2的小数部分是a,7-的小数部分为b.那a+b=(3)、已知的整数部分为x,的小数部分为y,求(y-)x-1的平方根.20. 在与之间,整数个数有个五、程序设计与实数运算
-
21. 有一个数值转换器,原理如下:

当输入的x=9时,输出的y等于( )
A、 B、± C、 D、22. 按下图所示程序框图计算,若输入的值为 , 则输出结果为( ) A、 B、 C、4 D、23. 按如图所示的程序计算,若开始输入的x的值是64,则输出的y的值是( )
A、 B、 C、4 D、23. 按如图所示的程序计算,若开始输入的x的值是64,则输出的y的值是( ) A、 B、 C、2 D、324. 如图是一个数据转换器,当输入的数x为4时,输出的y的值为;若输入有效的x后,始终输不出y的值,则满足条件的x的值为.
A、 B、 C、2 D、324. 如图是一个数据转换器,当输入的数x为4时,输出的y的值为;若输入有效的x后,始终输不出y的值,则满足条件的x的值为. 25. 有一个数值转换器,原理如图所示,当输入的x的值为64时,输出的y值是( )
25. 有一个数值转换器,原理如图所示,当输入的x的值为64时,输出的y值是( )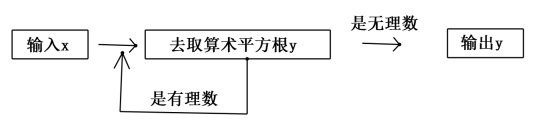 A、8 B、 C、 D、26. 有一个数值转换器原理如下:当输入x=16时,输出的数是( )
A、8 B、 C、 D、26. 有一个数值转换器原理如下:当输入x=16时,输出的数是( ) A、8 B、2 C、 D、
A、8 B、2 C、 D、六、新定义下的实数运算
-
27. 定义为不大于x的最大整数,如 , , , 则满足 , 则的最大整数为.28. 阅读下面文字,然后回答问题.
给出定义:一个实数的整数部分是不大于这个数的最大数,这个实数的小数部分为这个数与它的整数部分的差的绝对值.例如:2.4的整数部分为2,小数部分为 ; 的整数部分为1,小数部分可用 表示;再如,﹣2.6的整数部分为﹣3,小数部分为 .由此我们得到一个真命题:如果 ,其中 是整数,且 ,那么 , .
(1)、如果 ,其中 是整数,且 ,那么 , ;(2)、如果 ,其中 是整数,且 ,那么 , ;(3)、已知 ,其中m是整数,且 ,求 的值;29. 对于有理数 、 ,定义 的含义为:当 时, ,例如: .已知 , ,且 和 为两个连续正整数,则 的立方根为( )A、 B、 C、 D、30. 设表示小于的最大整数,如 , , 则下列结论中正确的是( )A、 B、的最小值是0 C、的最大值是1 D、不存在实数 , 使31. 规定符号[a]表示实数a的整数部分,[]=0,[4.15]=4.按此规定[+2]的值为 .七、综合训练
-
32. 计算33. 实数a,b,c在数轴上对应的点的位置如图所示,如果 , 那么下列各式正确的是( )
 A、 B、 C、 D、34. 与最接近的整数是( )A、2 B、3 C、4 D、1035. 如图,数轴上的三个点A,B,C分别表示实数a,b,c.
A、 B、 C、 D、34. 与最接近的整数是( )A、2 B、3 C、4 D、1035. 如图,数轴上的三个点A,B,C分别表示实数a,b,c. (1)、如果点C是的中点,那么a,b,c之间的数量关系是;(2)、比较与的大小,并说明理由;(3)、化简: .36. 数轴上1,的点分别为A和B,若A为BC的中点,则点C表示的数是( )A、 B、 C、 D、37. 已知 , 均为有理数,且 , 则 , 的值分别为( )A、3, B、 , 1 C、1, D、 , 338. 根据下表回答问题:
(1)、如果点C是的中点,那么a,b,c之间的数量关系是;(2)、比较与的大小,并说明理由;(3)、化简: .36. 数轴上1,的点分别为A和B,若A为BC的中点,则点C表示的数是( )A、 B、 C、 D、37. 已知 , 均为有理数,且 , 则 , 的值分别为( )A、3, B、 , 1 C、1, D、 , 338. 根据下表回答问题:16
16.1
16.2
16.3
16.4
16.5
16.6
16.7
16.8
256
259.21
262.44
265.69
268.96
272.25
275.56
278.89
282.24
(1)、265.69的平方根是;(2)、 , , ;(3)、设 的整数部分为 ,求 的立方根.39. 下列说法:①有理数与数轴上的点是一一对应的;②无理数与数轴上的点是一一对应的;③每一个实数都能在数轴上找到对应的点;④数轴上的每一个点都对应一个实数.其中正确的说法有( )A、4个 B、3个 C、2个 D、1个