2022~2023学年安徽省中考数学优质仿真模拟卷(二)
试卷更新日期:2023-05-10 类型:中考模拟
一、单选题(每题4分,共40分)
-
1. 下列说法正确的是( )A、两个数的和为零,则它们互为相反数 B、负数的倒数一定比原数大 C、π的相反数是-3.14 D、原数一定比它的相反数小2. 2022年杭州市的GDP达到18800亿元,用科学记数法表示“18800亿”正确的是( )A、0.188×1013 B、1.88×1012 C、1.88×1013 D、1.818×10143. 下列计算结果正确的是( )A、 B、 C、 D、4. 我市江华县有“神州摇都”的美涨,每逢“盘王节”会表演长鼓舞,长鼓舞中使用的“长鼓”内腔挖空,两端相通,两端鼓口为圆形,中间鼓腰较为细小.如图为类似“长鼓”的几何体,其俯视图的大致形状是( ).

 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,烧杯内液体表面与烧杯下底部平行,光线从液体中射向空气时发生折射,光线变成 , 点在射线上.已知 , , 则( )
5. 如图,烧杯内液体表面与烧杯下底部平行,光线从液体中射向空气时发生折射,光线变成 , 点在射线上.已知 , , 则( ) A、 B、 C、 D、6. 下列语句中,正确的有( )A、圆是轴对称图形,任何一条直径都是它的对称轴 B、平分弦的直径垂直于弦 C、在同圆或等圆中,相等的圆心角所对的弧相等 D、长度相等的两条弧相等7. 一个容器内有进水管和出水管,开始4min内只进水不出水,在随后的8min内既进水又出水,第12min后只出水不进水.进水管每分钟的进水量和出水量每分钟的出水量始终不变,容器内水量 (单位:L)与时间 (单位:min)之间的关系如图所示.
A、 B、 C、 D、6. 下列语句中,正确的有( )A、圆是轴对称图形,任何一条直径都是它的对称轴 B、平分弦的直径垂直于弦 C、在同圆或等圆中,相等的圆心角所对的弧相等 D、长度相等的两条弧相等7. 一个容器内有进水管和出水管,开始4min内只进水不出水,在随后的8min内既进水又出水,第12min后只出水不进水.进水管每分钟的进水量和出水量每分钟的出水量始终不变,容器内水量 (单位:L)与时间 (单位:min)之间的关系如图所示.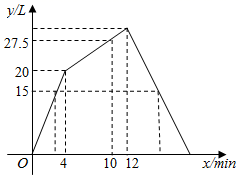
根据图象有下列说法:①进水管每分钟的进水量为5L;② 时, ;③当 时, ;④当 时, ,或 .其中正确说法的个数是( )
A、1个 B、2个 C、3个 D、4个8. 在四张完全相同的卡片上,分别画有圆,等腰三角形,直角三角形,菱形,现从中随机抽取一张,卡片上的图形恰好是中心对称图形的概率是( )A、 B、 C、 D、19. 关于x的方程(x﹣1)(x+2)=p2(p为常数)的根的情况,下列结论中正确的是( )A、两个正根 B、两个负根 C、一个正根,一个负根 D、无实数根10. 如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )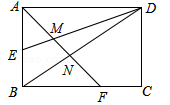 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空5分,共20分)
-
11. 因式分解:x3–x= .12. 如图,是的直径,与相切于点A, , 的延长线交于点P,则的度数是.
 13. 如图,点A是反比例函数y= (x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB= .点C是反比例函数y= (x>0)图象上一动点,连接AC,OC,若△AOC的面积为 ,则点C的坐标为 .
13. 如图,点A是反比例函数y= (x>0)图象上一点,过点A作AB⊥x轴于点B,连接OA,OB,tan∠OAB= .点C是反比例函数y= (x>0)图象上一动点,连接AC,OC,若△AOC的面积为 ,则点C的坐标为 .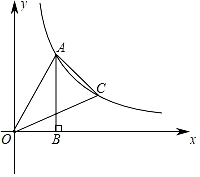 14. 关于的二次函数 , 在时有最大值6,则 .
14. 关于的二次函数 , 在时有最大值6,则 .三、解答题(共9题,共90分)
-
15. 解不等式 .16. 《孙子算经》中有一道题目:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺,木长几何?”题大意为:“现在有一根长木,不知道它的长度.用绳子去量这根长木,绳子还剩余4.5尺,将绳子对折后再量这根长木,长木还剩下1尺,问长木长多少尺?”请你用所学知识,求出长木长多少尺?17. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
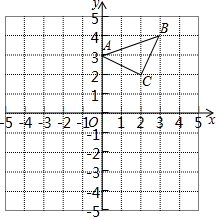
( 1 )画出△ABC向下平移4个单位长度得到的△A1B1C1;
( 2 )以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且位似比为2:1;
(3)△A2B2C2的面积是 ▲ 平方单位.18. 为了提高动手操作能力,安徽某学校九年级学生利用课后服务时间进行拼图大赛,他们用边长相同的正方形和正三角形进行拼接,赛后整理发现一组有规律的图案,如图所示.【观察思考】
第1个图案有4个正三角形,第2个图案有7个正三角形,第3个图案有10个正三角形,…依此类推

【规律总结】
(1)、第5个图案有个正三角形(2)、第n个图案中有个正三角形,(用含n的代数式表示)(3)、【问题解决】现有2023个正三角形,若按此规律拼第n个图案,要求正三角形一次用完,则该图案需要正方形多少个?
19. 如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF,BF,DF. (1)、求证:△ABC≌△ABF;
(1)、求证:△ABC≌△ABF;
(2)、当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.20. 如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4 米. (1)、求新传送带AC的长度.
(1)、求新传送带AC的长度.
(2)、如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点5米的货物MNQP是否需要挪走,并说明理由.参考数据: .
21. 某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛,特为甲、乙两名队员举行了一次选拔赛,要求这两名队员各射击10次.比赛结束后,根据比赛成绩情况,将甲、乙两名队员的比赛成绩制成了如下的统计图(表):甲队员的成绩统计表
成绩(单位:环)
7
8
9
10
次数(单位:次)
5
1
2
2
 (1)、在图1中,求“8环”所在扇形的圆心角的度数;(2)、经过整理,得到的分析数据如表,求表中的a、b、c的值.
(1)、在图1中,求“8环”所在扇形的圆心角的度数;(2)、经过整理,得到的分析数据如表,求表中的a、b、c的值.队员
平均数
中位数
众数
方差
甲
8
7.5
7
c
乙
a
b
7
1
(3)、根据甲、乙两名队员的成绩情况,该射击队准备选派乙参加比赛,请你写出一条射击队选派乙的理由.22. 在平面直角坐标系中,已知点 , 直线经过点A,抛物线恰好经过A,B,C三点中的两点.(1)、求直线的解析式;(2)、求a,b的值;(3)、平移抛物线 , 使其顶点仍在直线上,求平移后所得抛物线与y轴交点纵坐标的最大值.23.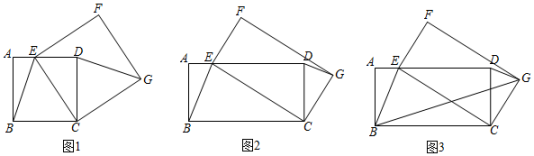 (1)、【问题情境】如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是;(2)、【类比探究】
(1)、【问题情境】如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是;(2)、【类比探究】如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;
(3)、【拓展提升】如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为 .