人教版七年级下数学期末复习知识点扫盲满分计划——5.3平行线性质
试卷更新日期:2023-05-10 类型:复习试卷
一、两直线平行,同位角相等
-
1. 如图,直线与相交于点 , , , , 求证:.

证明:已知 ,
( )
已知 ,
▲ ( )
已知 ,
( )
即 ▲ .
▲ ( )
( )
2. 如图,点E、F分别在AB、CD上,AF⊥CE于点O,∠l=∠B,∠A+∠2=90°,求证:AB∥CD.请完善解答过程,并在括号内填写相应的依据.
证明:∵AF⊥CE (已知),
∴∠AOE=90° ( )
又,∵∠1=∠B(已知)
∴ ▲ ∥ ▲ (同位角相等,两直线平行),
∴∠AFB=∠AOE( )
∴∠AFB= ▲ °,
又∵∠AFC+∠AFB+∠2=180°(平角的定义)
∴∠AFC+∠2= ▲ °
又∵∠A+∠2=90° (已知)
∴∠A=∠AFC ( )
∴AB∥CD.( )
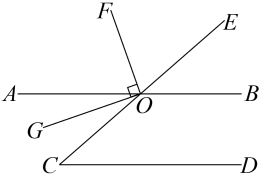
3. 如图, , . (1)、求证:;(2)、若 , , 求的度数.4. 如图,已知 , , 求的大小.
(1)、求证:;(2)、若 , , 求的度数.4. 如图,已知 , , 求的大小.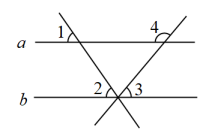 5. 如图,BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H,∠3+∠4=180°,试说明∠1=∠2.
5. 如图,BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H,∠3+∠4=180°,试说明∠1=∠2.
二、两直线平行,内错角相等
-
6. 完成下面的证明:
已知:如图, , .
求证:.
证明:∵(已知),
∴ ▲ // ▲ ( ).
∴( ).
又∵(已知),
∴( ).
即.
∴ ▲ // ▲ ( ).
∴(两直线平行,内错角相等).
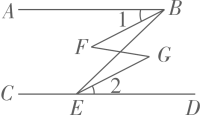
7. 如图,已知∠ABC+∠DCB=180°且∠1=∠2,试说明∠GFA+∠FDB=180°,请将下面的说明过程填写完整.
解:∵∠ABC+∠DCB=180°
∴CG∥AB,
∴∠1=∠FEA,( )
∵∠1=∠2,∴∠2=∠FEA,( )
∴EG∥ ▲ , ( )
∴ ▲ +∠FDB=180°,
∵∠GFA=∠DFE,( )
∴∠GFA+∠FDB=180°.
8. 如图,一块含有45°角的直角三角板的两个顶点放在直尺的对边上.若∠1=21°,则∠2度数为( )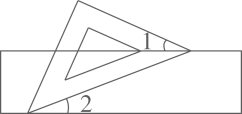 A、21° B、22° C、23° D、24°9. 如图,AB⊥AC,点D、E分别在线段AC、BF上,DF、CE分别与AB交于点M、N,若∠1=∠2,∠C=∠F,求证;AB⊥BF.请完善解答过程,并在括号内填写相应的依据.
A、21° B、22° C、23° D、24°9. 如图,AB⊥AC,点D、E分别在线段AC、BF上,DF、CE分别与AB交于点M、N,若∠1=∠2,∠C=∠F,求证;AB⊥BF.请完善解答过程,并在括号内填写相应的依据.
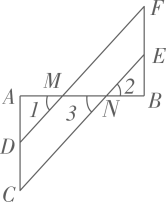
证明:∵∠1=∠2,∠2=∠3,
∴∠1=∠ ▲ . (等量代换)
∴DF∥CE( )
∴∠ADM=∠ ▲ (两直线平行,同位角相等)
∵∠C=∠F,(已知)
∴∠ADM=∠ ▲ (等量代换)
∴AC∥BF( )
∴∠A=∠B( )
∵AB⊥AC,(已知)
∴∠A=90°.
∴∠B=90°.
∴AB⊥BF.( )
10. 如图,∠ABC+∠ECB=180°,∠P=∠Q.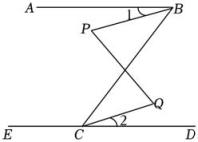
求证:∠1=∠2.
根据图形和已知条件,请补全下面这道题的解答过程.
证明:∵∠ABC+∠ECB=180°( ),
∴AB∥ED( ).
∴∠ABC=∠BCD( ).
又∵∠P=∠Q(已知),
∴PB∥ ▲ .
∴∠PBC= ▲ .
又∵∠1=∠ABC- ▲ , ∠2=∠BCD- ▲ ,
∴∠1=∠2(等量代换).
三、两直线平行,同旁内角互补
-
11. 已知,和中, , 试探究:
 (1)、如图1,与的关系是 ;(2)、如图2,写出与的关系,并说明理由.12. 如图, , .若 , 则的大小为( )
(1)、如图1,与的关系是 ;(2)、如图2,写出与的关系,并说明理由.12. 如图, , .若 , 则的大小为( ) A、 B、 C、 D、13. 已知直线 , 将含有的直角三角尺按如图方式放置(),其中A,C两点分别落在直线m,n上,若 , 则的度数为( )
A、 B、 C、 D、13. 已知直线 , 将含有的直角三角尺按如图方式放置(),其中A,C两点分别落在直线m,n上,若 , 则的度数为( )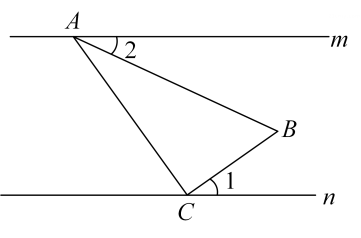 A、 B、 C、 D、14. 如图,AF的延长线与BC的延长线交于点E,AD∥BE,∠1=∠2,∠3=∠4.
A、 B、 C、 D、14. 如图,AF的延长线与BC的延长线交于点E,AD∥BE,∠1=∠2,∠3=∠4. (1)、求证:AB∥DC;(2)、若∠B=78°,∠E=25°,求∠CAE的度数.15. 如图,已知 , , 点是射线上一动点(与点不重合), , 分别平分和 , 交射线于点 , .
(1)、求证:AB∥DC;(2)、若∠B=78°,∠E=25°,求∠CAE的度数.15. 如图,已知 , , 点是射线上一动点(与点不重合), , 分别平分和 , 交射线于点 , .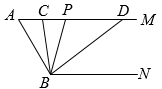 (1)、求的度数;(2)、在点运动过程中,试判断与之间的数量关系?并说明理由;(3)、当点运动到使时,求出的度数.
(1)、求的度数;(2)、在点运动过程中,试判断与之间的数量关系?并说明理由;(3)、当点运动到使时,求出的度数.四、平行线的拐点辅助线
-
16. 已知点C在射线OA上.
 (1)、如图①,CD∥OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)、在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示);(3)、在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.17. 某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知 , , , 则 .
(1)、如图①,CD∥OE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;(2)、在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示);(3)、在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.17. 某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知 , , , 则 . 18. 如图,AB∥DE,BC⊥CD,则以下说法中正确的是( )
18. 如图,AB∥DE,BC⊥CD,则以下说法中正确的是( ) A、α,β的角度数之和为定值 B、α随β增大而增大 C、α,β的角度数之积为定值 D、α随β增大而减小19. 如图,直线AB//CD, , , 则.
A、α,β的角度数之和为定值 B、α随β增大而增大 C、α,β的角度数之积为定值 D、α随β增大而减小19. 如图,直线AB//CD, , , 则. 20. 如图
20. 如图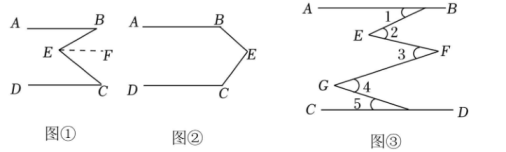 (1)、问题发现:
(1)、问题发现:如图①,直线AB∥CD,连接BE,CE,可以发现∠B+∠C=∠BEC.请把下面的证明过程补充完整:
证明:过点E作EF∥AB,
∵AB∥DC (已知)
∴EF∥DC( ).
∴∠C=∠CEF.( ).
∵EF∥AB,
∴∠B=∠BEF(同理).
∴∠B+∠C= ▲ (等量代换).即∠B+∠C=∠BEC.
(2)、拓展探究:如果点E运动到图②所示的位置,其他条件不变,说明:∠B+∠C+∠BEC=360°.
(3)、解决问题:如图③,AB∥DC,E、F、G是AB与CD之间的点,直接写出∠1,∠2,∠3,∠4,∠5之间的数量关系.五、综合训练
-
21. 如图,直线 , 直线与 , 分别交于点 , , .小安将一个含角的直角三角板按如图①放置,使点、分别在直线、上,且在点、的右侧, , .


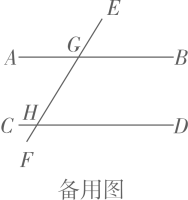 (1)、填空; (填“”“ ”或“=” );(2)、若的平分线交直线于点 , 如图②.
(1)、填空; (填“”“ ”或“=” );(2)、若的平分线交直线于点 , 如图②.①当 , 时,求的度数;
②小安将三角板沿直线左右移动,保持 , 点、分别在直线和直线上移动,请直接写出的度数(用含的式子表示).
22. 如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(点P与点A不重合),BC、BD分别平分∠ABP和∠PBN. (1)、求∠ABN的度数;(2)、当点P运动时,∠CBD的度数是否随之发生变化?若不变化,请求出它的度数;若变化,请写出变化规律;(3)、当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.23. 如图,在四边形中, , 平分 , , , 点H在直线上,满足. 若 , 则k的值是( )
(1)、求∠ABN的度数;(2)、当点P运动时,∠CBD的度数是否随之发生变化?若不变化,请求出它的度数;若变化,请写出变化规律;(3)、当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.23. 如图,在四边形中, , 平分 , , , 点H在直线上,满足. 若 , 则k的值是( ) A、和 B、和 C、和 D、和24. 如图1,直线与直线交于点O,().小明将一个含 , 的直角三角板如图1所示放置,使顶点P落在直线上,过点Q作直线交直线于点H(点H在Q左侧).
A、和 B、和 C、和 D、和24. 如图1,直线与直线交于点O,().小明将一个含 , 的直角三角板如图1所示放置,使顶点P落在直线上,过点Q作直线交直线于点H(点H在Q左侧). (1)、若 , , 求的度数.(2)、如图2,若的角平分线交直线于点E.
(1)、若 , , 求的度数.(2)、如图2,若的角平分线交直线于点E.①当 , 时,求证:.
②小明将三角板保持并向左平移,运动过程中,探究与之间的数量关系,并说明理由.
25. 已知点E在直线AB,CD之间,且∠BAE=∠AEC-∠ECD. (1)、如图1,求证:AB∥CD;(2)、若AH平分∠BAE,FG∥CE.
(1)、如图1,求证:AB∥CD;(2)、若AH平分∠BAE,FG∥CE.①如图2,若∠AEC=98°,FH平分∠DFC,求∠AHF的度数;
②如图3,若FH平分∠CFC,试判断∠AHF与∠AEC的数量关系并说明理由.
26. 如图,已知 , , BC与b相交,若 , 则的度数为. 27. 如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B.
27. 如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°,试说明:∠GDC=∠B. 28. 问题情境:如图1, , , , 求的度数.小明的思路是过点作 , 通过平行线的性质来求.
28. 问题情境:如图1, , , , 求的度数.小明的思路是过点作 , 通过平行线的性质来求.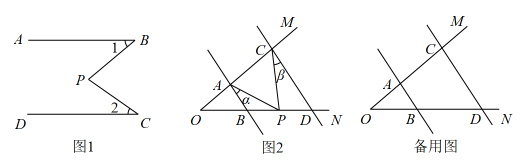 (1)、按照小明的思路,则的度数为;(2)、问题迁移:如图2, , 点在射线上运动,记 , .当点在、两点之间运动时,问与、之间有何数量关系?请说明理由;(3)、在(2)的条件下,如果点不在、两点之间运动时(点与点、、三点不重合),写出与、之间的数量关系,并说明理由.
(1)、按照小明的思路,则的度数为;(2)、问题迁移:如图2, , 点在射线上运动,记 , .当点在、两点之间运动时,问与、之间有何数量关系?请说明理由;(3)、在(2)的条件下,如果点不在、两点之间运动时(点与点、、三点不重合),写出与、之间的数量关系,并说明理由.