人教版七年级下数学期末复习知识点扫盲满分计划——5.2平行线
试卷更新日期:2023-05-10 类型:复习试卷
一、平行公理及应用:平行于同一条直线的两条直线平行
-
1. 图,在同一平面内过点且平行于直线的直线有( )
 A、0条 B、1条 C、2条 D、无数条2. 直线a、b、c中,a∥b,b∥c,则直线a与直线c的关系是( )A、相交 B、平行 C、垂直 D、不确定3. 为增强学生体质,某学校将“抖空竹”引入阳光体育一小时活动.图1是一位同学抖空竹时的一个瞬间,数学老师把它抽象成图2的数学问题:已知AB∥CD,∠EAB=80°,∠ECD=110°.求∠AEC的度数.小明在解决过程中,过E点作EF∥CD,则可以得到EF∥AB,其理由是 , 根据这个思路可得∠AEC=°.
A、0条 B、1条 C、2条 D、无数条2. 直线a、b、c中,a∥b,b∥c,则直线a与直线c的关系是( )A、相交 B、平行 C、垂直 D、不确定3. 为增强学生体质,某学校将“抖空竹”引入阳光体育一小时活动.图1是一位同学抖空竹时的一个瞬间,数学老师把它抽象成图2的数学问题:已知AB∥CD,∠EAB=80°,∠ECD=110°.求∠AEC的度数.小明在解决过程中,过E点作EF∥CD,则可以得到EF∥AB,其理由是 , 根据这个思路可得∠AEC=°. 4. 下列语句:
4. 下列语句:①不相交的两条直线叫平行线
②在同一平面内,两条直线的位置关系只有两种:相交和平行
③如果线段AB和线段CD不相交,那么直线AB和直线CD平行
④如果两条直线都和第三条直线平行,那么这两条直线平行
⑤过一点有且只有一条直线与已知直线平行
正确的个数是( )
A、1 B、2 C、3 D、45. 已知直线a∥b,b∥c,c∥d,则a与d的关系是什么?为什么?二、平行判定:同位角相等,两直线平行
-
6. 如图AF 与BD相交于点C,∠B=∠ACB, 且CD平分∠ECF.求证: .
请完成下列推理过程:
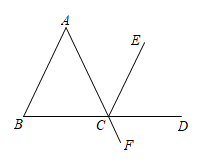
证明:∵CD 平分∠ECF
∴∠ECD= ▲ ( )
∵∠ACB=∠FCD( )
∴∠ECD=∠ACB( )
∵∠B=∠ACB
∴∠B=∠▲( )
∴ ( ).
7. 如图,∠B+∠BAD=180°,∠1=∠2. 求证:ABCD.请将下面的证明过程补充完整.
证明:
∵∠B+∠BAD=180°(已知),
∠1+∠BAD=180°( ),
∴∠1=∠B( ).
∵∠1=∠2(已知),
∴∠2=_▲_( ).
∴ABCD( ).
8. 已知:如图,CF平分∠ACM,∠1=72°,∠2=36°,判断CM与DN是否平行,并说明理由. 9. 把下面的说理过程补充完整:
9. 把下面的说理过程补充完整:已知,如图,直线AB,CD被直线EF所截,点H为CD与EF的交点,GH⊥CD于点H,∠2=30°,∠1=60°.试说明: .
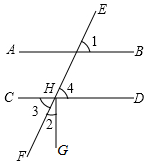
解:∵GH⊥CD( ),
∴∠CHG=90°( ).
又∵∠2=30°( ),
∴∠3=( ).
∴∠4=60°( ).
又∵∠1=60°( ),
∴∠1=∠4( ).
∴( ).
10. 如图所示,直线AB,CD相交于点O,OD平分.∠EOB,OF平分∠AOE,GH⊥CD,垂足为点H,GH与FO平行吗?说明理由.
三、平行判定:内错角相等,两直线平行
-
11. 如图,AB⊥ BC,BC⊥ CD,且∠ 1=∠ 2,证明:EB∥ CF
 12. 完成下面推理填空:
12. 完成下面推理填空:如图,E,F分别在AB和CD上, , 与互余,于G.
求证: .

证明:∵ , ∴( ),
∵(已知),∴ ▲ ▲ ( ),
∴( ),
∵(平角的定义),∴ .
∵与互余(已知),∴(互余的定义),
∴( ),∴( ).
13. 将一幅三角板拼成如图的图形,过点C作CF平分∠DCE交DE于点F.试说明CF∥AB的理由.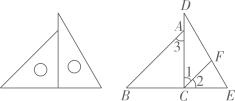 14. 完成下面的说理过程:如图,在四边形中,E、F分别是 , 延长线上的点,连接 , 分别交 , 于点G、H.已知 , , 对和说明理由.
14. 完成下面的说理过程:如图,在四边形中,E、F分别是 , 延长线上的点,连接 , 分别交 , 于点G、H.已知 , , 对和说明理由.
理由:∵(已知),
( ),
∴(等量代换).
∴( ).
∵( ).
∵(已知),
∴.( ).
∴( ).
15. 已知:如图,直线EF分别与直线AB,CD相交于点P,Q,PM垂直于EF,∠1+∠2=90°.求证:AB//CD.
四、平行判定:同旁内角互补两直线平行
-
16. 已知:如图.在△ABC中.点D,E,F分到在边AB,AC,BC上,CD与EF相交于点H,且∠BDC+∠DHF=180°.∠DEF=∠B,求证:DE∥BC.
 17. 如图,分别平分和 , 且 , 求证: .
17. 如图,分别平分和 , 且 , 求证: .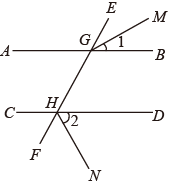 18. 如图所示,AD与BE相交于点F,∠A=∠C,∠1与∠2互补,求证:ABCE.
18. 如图所示,AD与BE相交于点F,∠A=∠C,∠1与∠2互补,求证:ABCE. 19. 如图,已知AE平分∠BAC交BC于点E,AF平分∠CAD交BC的延长线于点F,∠B=64°,∠EAF=58°,试判断AD与BC是否平行.
19. 如图,已知AE平分∠BAC交BC于点E,AF平分∠CAD交BC的延长线于点F,∠B=64°,∠EAF=58°,试判断AD与BC是否平行.
解:∵AE平分∠BAC,AF平分∠CAD(已知),
∴∠BAC=2∠1,∠CAD= ▲ ( ).
又∵∠EAF=∠1+∠2=58°,
∴∠BAD=∠BAC+∠CAD
=2(∠1+∠2)
= ▲ °(等式性质).
又∵∠B=64°(已知),
∴∠BAD+∠B= ▲ °.
∴ ▲ ▲ ( ).
20. 在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线、 , 并说出自己做法的依据。小琛、小萱、小冉三位同学的做法如下:
小琛说:“我的做法的依据是内错角相等,两直线平行”
小琛说的是否正确?(回答正确或错误)
小萱做法的依据是
小冉做法的依据是 .
五、平面内垂直于同一条直线的两条直线平行
-
21. 命题:直线a、b、c,若a⊥b,c⊥b,则a//c;则此命题为 命题.(填真或假)22. 已知四条直线a,b,c,d在同一平面内,a⊥b,b⊥c,c⊥d,则下列式子成立的是( )A、a⊥c B、b⊥d C、a⊥d D、a∥d23. 如图, , , , 垂足分别为点F,E,求证: .
 24. 如图,已知AD⊥BC , FG⊥BC , 垂足分别为D , G.且∠1=∠2,猜想:DE与AC有怎样的关系?说明理由.
24. 如图,已知AD⊥BC , FG⊥BC , 垂足分别为D , G.且∠1=∠2,猜想:DE与AC有怎样的关系?说明理由.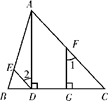 25. 如图, , , 于点 .求证: .
25. 如图, , , 于点 .求证: .
六、综合训练
-
26. 如图所示,已知∠1=∠A,∠2=∠B,要证MN//EF.请完善证明过程.并在括号内填上相应依据.

证明:∵∠1=∠A(已知),
∴ ()。
∵∠2=∠B(已知),
∴(),
∴MN∥EF()
27. 已知:如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.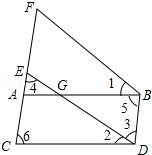 28. 如图,F是上一点,于点是上一点,于点 , 求证: .
28. 如图,F是上一点,于点是上一点,于点 , 求证: . 29. 如图,三角形ABC中,AC=BC , D是BC上的一点,连接AD , DF平分∠ADC交∠ACB的外角∠ACE的平分线于F . 求证:CF AB .
29. 如图,三角形ABC中,AC=BC , D是BC上的一点,连接AD , DF平分∠ADC交∠ACB的外角∠ACE的平分线于F . 求证:CF AB . 30. 推理填空
30. 推理填空如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,求证:CE∥DF.请完成下面的解题过程.

解:∵BD平分∠ABC,CE平分∠ACB ( 已知 )
∴∠DBC= ∠_▲_,∠ECB= ∠_▲_( 角平分线的定义)
又∵∠ABC=∠ACB (已知)
∴∠_▲_=∠_▲_.
又∵∠_▲_=∠_▲_ (已知)
∴∠F=∠_▲_
∴CE∥DF_▲__.
31. 完成下面的证明.已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵AB∥CD(已知)
∴∠4=∠ , .
∵∠3=∠4(已知)
∴∠3=∠ , .
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF
即:∠=∠ .
∴∠3=∠ .
∴AD∥BE.
 32. MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由.
32. MF⊥NF于F,MF交AB于点E,NF交CD于点G,∠1=140°,∠2=50°,试判断AB和CD的位置关系,并说明理由. 33. 如图,已知:CD⊥AB于点D,EF⊥AB于点F,∠1=∠2.
33. 如图,已知:CD⊥AB于点D,EF⊥AB于点F,∠1=∠2.求证:DG∥BC.
 34. 如图,直线AB,CD相交于点O,OD平分∠EOB,OF平分∠AOE,GH⊥CD,垂足为H,求证:GH∥FO.
34. 如图,直线AB,CD相交于点O,OD平分∠EOB,OF平分∠AOE,GH⊥CD,垂足为H,求证:GH∥FO. 35.
35.如图,∠E=∠1,∠3+∠ABC=180°,BE是∠ABC的角平分线.你能判断DF与AB的位置关系吗?请说明理由.
 36. 如图∠1+∠2=180°, , 判断图中有哪些直线平行?并给予说理.
36. 如图∠1+∠2=180°, , 判断图中有哪些直线平行?并给予说理. 37. 阅读下面的解答过程,并填空.
37. 阅读下面的解答过程,并填空.如图, , 平分 , 平分 , . 求证: .

证明:∵平分 , 平分 , (已知)
∴ ▲ , ▲ . (角平分线的定义)
又∵ , (已知)
∴∠ ▲ =∠ ▲ . (等量代换)
又∵ , (已知)
∴∠ ▲ ∠ ▲ . (等量代换)
∴ . ( )
38. 如图直角三角形ABC中, , 平分 , ,求证: .

