初中数学同步训练必刷题(人教版七年级下册 9.3 一元一次不等式组)
试卷更新日期:2023-05-10 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 下列不等式组中,是一元一次不等式组的是( )
A、 B、 C、 D、2. x是不大于5的正数,则下列表示正确的是( )A、0<x<5 B、0<x≤5 C、0≤x≤5 D、x≤53. 不等式组的解集在数轴上表示为( )A、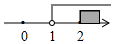 B、
B、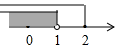 C、
C、 D、
D、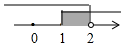 4. 橘子是我们常见的一种水果,取5个大小均等的橘子放在同一简易天平秤,如图,则估计一个橘子的重量大约是( )
4. 橘子是我们常见的一种水果,取5个大小均等的橘子放在同一简易天平秤,如图,则估计一个橘子的重量大约是( ) A、20 B、30 C、40 D、455. 已知关于x的不等式组有四个整数解,则m的取值范围是( )A、 B、 C、 D、6. 已知不等式组解集为 , 则的值为( )A、1 B、2022 C、-1 D、-20227. 运行程序如图所示,规定:从“输入一个值x”到“结果是否95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )
A、20 B、30 C、40 D、455. 已知关于x的不等式组有四个整数解,则m的取值范围是( )A、 B、 C、 D、6. 已知不等式组解集为 , 则的值为( )A、1 B、2022 C、-1 D、-20227. 运行程序如图所示,规定:从“输入一个值x”到“结果是否95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( ) A、 B、 C、 D、8. 下列属于一元一次不等式组的是( )A、 B、 C、 D、9. 若关于x的不等式组的解集为﹣3<x<2,则a+b的值为( )A、﹣5 B、5 C、6 D、﹣610. 把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本,共有( )名同学.A、5 B、6 C、7 D、8
A、 B、 C、 D、8. 下列属于一元一次不等式组的是( )A、 B、 C、 D、9. 若关于x的不等式组的解集为﹣3<x<2,则a+b的值为( )A、﹣5 B、5 C、6 D、﹣610. 把一些书分给几名同学,如果每人分3本,那么余8本;如果前面的每名同学分5本,那么最后一人就分不到3本,共有( )名同学.A、5 B、6 C、7 D、8二、填空题(每空3分,共30分)
-
11. 某方便面外包装标明“净含量为250g10g”,用不等式表示这袋方便面的净含量x是 .12. 一元一次不等式组的数集为 .13. 如果不等式组有解,那么m的取值范围是 .14. 若关于x的不等式组的解集为x>a,则字母a的取值范围是 .15. 已知点P(2-a,3a)在第二象限,那么a的取值范围是 .16. 已知关于 , 的方程组的解为整数,且关于的不等式组有且仅有3个整数解,则所有满足条件的整数a的和为.17. 把一筐苹果分给几个学生,如果每人分3个,那么余8个;如果每人分5个,那么最后一人分到,但不足3个.设学生有x人,列不等式组为 .18. 已知 , 且 , 那么的取值范围为 .19. 若关于x的不等式组 , 有且只有三个整数解,则n的取值范围是 .20. 运行程序如图所示,规定:从“输入一个值x”到“结果是否>5”为一次程序操作,如果程序操作进行了两次才停止,那么x的取值范围是 .

三、解答题(共6题,共60分)
-
21. 解下列不等式(组),并把解集在数轴上表示出来.(1)、1+>5-(2)、22. 已知 .(1)、请用含x的式子表示y;(2)、当时,求x的最大值.23. 已知关于x的不等式组(1)、当时,求该不等式组的整数解;(2)、若原不等式组的整数解只有7,8,求m的取值范围.24. 为鼓励学生参加体育锻炼,学校体育组准备购买一批篮球和排球.已知篮球的单价比排球的单价多15元/个,买2个排球和3个篮球一共需要220元.(1)、篮球和排球的单价分别是多少元?(2)、体育组购买的篮球和排球总数量是36个,其中篮球的数量比排球的2倍还多,购买总资金不超过1700元,有几种购买方案?25. 某景区的门票每张8元,一次性使用,考虑到人们的不同需求,也为了吸引更多的游客,该景区除保留原来的售票方法外,还推出了一种“购买个人年票”(个人年票从购买日起,可供持票者使用一年)的售票方法,年票分A,B,C三类:A类年票每张100元,持票者进入景区时,无需再购买门票;B类年票每张50元,持票者进入该景区时,需再购买门票,每次2元;C类年票每张20元,持票者进入该景区时,需再购买门票,每次3元.(1)、如果只能选择一种购买门票的方式,并且计划在一年中花费80元在该景区的门票上,通过计算,找出可进入该景区次数最多的方式.(2)、一年中进入该景区不少于多少次时,购买A类年票比较合算?26. 先阅读理解下面的例题,再按要求解答下列问题.
例题:解不等式 .
解:由有理数的乘法法则“两数相乘,同号得正,异号得负”,得 , , 解不等式组 , 得 , 解不等式组 , 得 , 的解集为或 .
(1)、满足的的取值范围是;(2)、仿照材料,解不等式 .