四川省攀枝花市2023届高三理数第三次统一考试试卷

试卷更新日期：2023-05-10 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $M = {x | - 1 < x \leq 3 ， x \in Z}$ ， $N = {x | (x + 1) (x - 2) \leq 0}$ ，则 $M \cap N =$ （）

A、 ${x | - 1 < x \leq 2}$ B、 ${- 1 ， 0 ， 1 ， 2}$ C、 ${0 ， 1 ， 2}$ D、 ${- 1 ， 0 ， 1 ， 2 ， 3}$

查看试题解析
2. 如果一个复数的实部和虚部相等，则称这个复数为“等部复数”，若复数 $z = \frac{i}{1 - a i}$ （i为虚数单位）为“等部复数”，则实数a的值为（）

A、-3 B、-1 C、0 D、1

查看试题解析
3. 攀枝花昼夜温差大，是内陆地区发展特色农业的天然宝地，干热河谷所孕育的早春蔬菜为大家送去新鲜优质的维生素和膳食纤维.下图为攀枝花 $2023$ 年 $3$ 月 $6$ 日至 $12$ 日的最高气温与最低气温的天气预报数据，下列说法错误的是（）

A、这 $7$ 天的单日最大温差为 $17$ 度的有 $2$ 天 B、这 $7$ 天的最高气温的中位数为 $29$ 度 C、这 $7$ 天的最高气温的众数为 $29$ 度 D、这 $7$ 天的最高气温的平均数为 $29$ 度

查看试题解析
4. 如图所示的程序框图中，若输出的函数值 $f (x)$ 在区间 $[- 3 ， 2]$ 内，则输入的实数x的取值范围是（）

A、 $[- 4 ， 1]$ B、 $[- 2 ， 4]$ C、 $[- 1 ， 4]$ D、 $[- 1 ， 2]$

查看试题解析
5. $(1 + \frac{1}{x}) (1 - 2 x)^{5}$ 的展开式中，常数项是（）

A、-9 B、-10 C、9 D、10

查看试题解析
6. 对于直线m和平面 $α$ ， $β$ ，下列命题中正确的是（）

A、若 $m / / α$ ， $α / / β$ ，则 $m / / β$ B、若 $m ⊥ β$ ， $α ⊥ β$ ，则 $m / / α$ C、若 $m ⊥ α$ ， $α / / β$ ，则 $m ⊥ β$ D、若 $m \subset α$ ， $α ⊥ β$ ，则 $m ⊥ β$

查看试题解析
7. 已知 $α$ 为锐角， $s i n α = \frac{3}{5}$ ，角 $β$ 的终边上有一点 $P (2 ， 1)$ ，则 $t a n (α + β) =$ （）

A、2 B、 $\frac{10}{11}$ C、 $\frac{11}{10}$ D、 $- \frac{11}{12}$

查看试题解析
8. 为落实立德树人的根本任务，践行五育并举，某学校开设 $A$ 、 $B$ 、 $C$ 三门德育校本课程，现有甲、乙、丙、丁四位同学报名参加校本课程的学习，每位同学仅报一门，每门至少有一位同学报名，则甲和乙都没选择 $A$ 门课程的不同报名种数为（）

A、12 B、14 C、16 D、18

查看试题解析
9. “绿水青山就是金山银山”理念已经成为全党全社会的共识和行动，工业废水中的某稀有金属对环境有污染，甲企业经过数年攻关，成功开发出了针对该金属的“废水微循环处理利用技术”，废水每通过一次该技术处理，可回收20%的金属．若当废水中该金属含量低于最原始的5%时，至少需要循环使用该技术的次数为（）（参考数据： $l g 2 \approx 0.301$ ）

A、12 B、13 C、14 D、15

查看试题解析
10. 已知函数 $f (x) = s i n (ω x + \frac{π}{3}) (ω > 0)$ 对任意 $x \in (0 ， \frac{3 π}{8})$ 都有 $f (x) > \frac{1}{2}$ ，则当 $ω$ 取到最大值时， $f (x)$ 图象的一条对称轴为（）

A、 $x = \frac{π}{8}$ B、 $x = \frac{3 π}{16}$ C、 $x = \frac{π}{2}$ D、 $x = \frac{3 π}{4}$

查看试题解析
11. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点分别为 $F_{1}$ 、 $F_{2}$ ，过 $F_{1}$ 作直线 $l$ ，使得它双曲线的一条渐近线垂直且垂足为点 $Q$ ， $l$ 与双曲线的右支交于点 $P$ ，若线段 $P Q$ 的垂直平分线恰好过 $C$ 的右焦点 $F_{2}$ ，则双曲线 $C$ 的离心率为（）

A、 $\frac{\sqrt{5}}{2}$ B、 $\frac{\sqrt{13}}{3}$ C、 $\frac{\sqrt{13}}{2}$ D、2

查看试题解析
12. 定义在 $R$ 上的连续可导函数 $f (x)$ 的导函数为 $f^{'} (x)$ ， $f (x)$ 满足 $f (1 - x) = f (x + 1)$ ，且 $y = f (4 x + 2)$ 为奇函数．当 $x \in (2 ， 3]$ 时， $f (x) = {(x - 2)}^{3} - 3 (x - 2)$ ，则 $f^{'} (2022) + f (2023) =$ （）

A、-5 B、-2 C、-1 D、1

查看试题解析

二、填空题

13. 已知实数x，y满足约束条件 ${\begin{array}{l} x - y \leq 0 \\ x + y \leq 1 \\ x \geq 0 \end{array}$ ，则 $z = x + 2 y$ 的最大值为.

查看试题解析
14. 已知抛物线 $C ： y^{2} = 4 x$ 的焦点为F，过F的直线l与C交于A，B两点，O为坐标原点，则 $\vec{O A} \cdot \vec{O B} =$ .

查看试题解析
15. 如图，圆台 $O_{1} O_{2}$ 中， $O_{1} O_{2} = \sqrt{5}$ ，其外接球的球心O在线段 $O_{1} O_{2}$ 上，上下底面的半径分别为 $r_{1} = 1$ ， $r_{2} = \sqrt{3}$ ，则圆台外接球的表面积为.

查看试题解析
16. 如图，圆的内接四边形 $A B C D$ 中， $A C$ 与 $B D$ 相交于点 $O$ ， $A C$ 平分 $∠ D A B$ ， $∠ A B C = \frac{π}{3}$ ， $A B = 3 B C = 3$ ．则 $△ A C D$ 的面积为．

查看试题解析

三、解答题

17. 某企业从生产的一批产品中抽取 $100$ 个作为样本，测量这些产品的一项质量指标值，由测量结果制成如图所示的频率分布直方图．

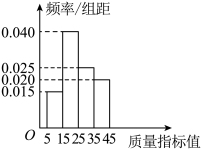(1)、求这 $100$ 件产品质量指标值的样本平均数 $\bar{x}$ （同一组数据用该区间的中点值作代表）和中位数；

(2)、已知某用户从该企业购买了 $3$ 件该产品，用 $X$ 表示这 $3$ 件产品中质量指标值位于 $[15 ， 25)$ 内的产品件数，用频率代替概率，求 $X$ 的分布列和数学期望．

查看试题解析
18. 已知等差数列 ${a_{n}}$ 的公差为 $d (d \neq 0)$ ，前n项和为 $S_{n}$ ，现给出下列三个条件：① $S_{1} ， S_{2} ， S_{4}$ 成等比数列；② $S_{4} = 32$ ；③ $S_{6} = 3 (a_{6} + 2)$ .请你从这三个条件中任选两个解答下列问题.

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $b_{n} - b_{n - 1} = 2 a_{n} (n \geq 2)$ ，且 $b_{1} = 3$ ，设数列 ${\frac{1}{b_{n}}}$ 的前n项和为 $T_{n}$ ，求证： $\frac{1}{3} \leq T_{n} < \frac{1}{2}$ .

查看试题解析
19. 如图1，圆的内接四边形ABCD中， $∠ D A C = 4 5^{∘}$ ， $∠ C A B = 6 0^{∘}$ ，直径 $A C = 2$ ．将圆沿AC折起，并连接OB、OD、BD，使得△BOD为正三角形，如图2．

(1)、证明：图2中的 $A B ⊥$ 平面BCD；

(2)、在图2中，求二面角 $O - B D - C$ 的余弦值．

查看试题解析
20. 已知椭圆 $C$ 的焦点坐标为 $F_{1} (- 2 ， 0)$ 和 $F_{2} (2 ， 0)$ ，且椭圆经过点 $G (2 ， \frac{\sqrt{5}}{5})$ ．

(1)、求椭圆 $C$ 的标准方程；

(2)、椭圆 $C$ 的上、下顶点分别为点 $M$ 和 $N$ ，动点 $A$ 在圆 $x^{2} + y^{2} = 1$ ，动点 $B$ 在椭圆 $C$ 上，直线 $M A ， M B$ 的斜率分别为 $k_{1} ， k_{2}$ ，且 $k_{1} = 5 k_{2}$ ．
（ⅰ）证明： $N ， A ， B$ 三点共线；
（ⅱ）求 $△ M A B$ 外接圆直径的最大值．

查看试题解析
21. 已知函数 $f (x) = x e^{x} - a l n x$ 在 $x = 1$ 处的切线方程为 $y = (2 e + 1) x - b (a ， b \in R)$

(1)、求实数 $a$ ， $b$ 的值；

(2)、设函数 $g (x) = f (x) - 2 e^{x} - x + 3$ ，当 $x \in [\frac{1}{2} ， 1]$ 时， $g (x)$ 的值域为区间 $(m ， n) (m ， n \in Z)$ 的子集，求 $n - m$ 的最小值．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，曲线 $C_{1}$ 的参数方程为 ${\begin{array}{l} x = t + \frac{1}{t} \\ y = t - \frac{1}{t} \end{array}$ （t为参数），曲线 $C_{2} ： {(x - 2)}^{2} + y^{2} = 4$ ，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系.

(1)、求 $C_{1}$ ， $C_{2}$ 的极坐标方程；

(2)、若射线 $θ = \frac{π}{6} (ρ \geq 0)$ 分别与曲线 $C_{1}$ ， $C_{2}$ 相交于A，B两点，求 $△ C_{2} A B$ 的面积.

查看试题解析
23. 已知函数 $f (x) = | x - 1 | + | x - 3 |$ .

(1)、解不等式 $f (x) \leq x + 1$ ；

(2)、设函数 $f (x)$ 的最小值为c，正实数a，b满足 $a + b = c$ ，求 $\frac{1}{a} + \frac{1}{b + 1}$ 的最小值.

查看试题解析