四川省名校联盟2023届高三理数下学期4月联考试卷

试卷更新日期：2023-05-10 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知 $(1 - i) z - 2 i = 2$ ，则 $| z | =$ （）

A、2 B、 $\frac{\sqrt{2}}{2}$ C、1 D、 $\frac{1}{2}$

查看试题解析
2. 设集合 $A = {x \in N^{*} | x^{2} - 2 x - 8 < 0}$ ， $B = {x | x - a > 0}$ ，集合 $A \cap B$ 中恰好含有2个元素，则实数a的取值范围为（）

A、 $(1 ， 2)$ B、 $[1 ， 2)$ C、 $(1 ， 2]$ D、 $[1 ， 2]$

查看试题解析
3. 我国古代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”，意思是说，有一块正方形田地，在其一角有一个圆形的水池（其中圆与正方形一角的两边均相切），如图所示．已知圆O的半径为2丈，过C作圆O的两条切线，切点分别为M，N，若 $M N = \sqrt{3} O M$ ，则对角线AC长度为（）

A、 $4 + 2 \sqrt{2}$ 丈 B、 $2 + \sqrt{2}$ 丈 C、 $10 - 2 \sqrt{2}$ 丈 D、 $2 + 4 \sqrt{2}$ 丈

查看试题解析
4. 国家统计局公报显示绘制出的2017-2021年每年本专科、中等职业教育及普通高中的招生人数（单位：万）统计图如下图所示，则下列关于2017-2021年说法正确的是（）

A、每年本专科、中等职业教育和普通高中的招生人数都在增长 B、中等职业教育和普通高中的招生人数差距最大的年份是2019年 C、本专科每年的招生人数增幅最大的年份是2018年 D、本专科的招生人数所占比例最高的年份是2021年

查看试题解析
5. 已知等比数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ， $a_{4} = 1$ ， $S_{8} = 3 (a_{2} + a_{4} + a_{6} + a_{8})$ ，则（）

A、 $a_{n} = 2^{n - 4}$ B、 $a_{n} = 2^{n + 4}$ C、 $S_{n} = 16 + 2^{4 - n}$ D、 $S_{n} = 16 - 2^{4 - n}$

查看试题解析
6. 设函数 $f (x) = \frac{x}{e^{x}}$ ，则曲线 $y = f (x)$ 在 $(- 1 ， f (- 1))$ 处的切线与两坐标轴围成的三角形面积为（）

A、e B、 $\frac{e}{2}$ C、 $\frac{e}{4}$ D、 $\frac{e}{8}$

查看试题解析
7. 函数 $f (x) = \frac{1}{3} x^{3} - \frac{l n | x |}{x}$ 的图象可能为（）

A、 B、 C、 D、

查看试题解析
8. 过抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点F的直线交抛物线于A，B点， $\vec{A F} = 3 \vec{F B}$ ，且 $| A B | = 8$ ，则 $p =$ （）

A、1 B、2 C、3 D、4

查看试题解析
9. 已知函数 $f (x) = c o s (ω x + \frac{2 π}{3}) (ω > 0)$ 在区间 $(a ， b)$ 内单调且 $b - a = \frac{π}{2}$ ，在区间 $(0 ， \frac{π}{3})$ 内存在最值点，则当 $ω$ 取得最大值时，满足 $f (x_{0}) = - \frac{\sqrt{3}}{2}$ 的一个 $x_{0}$ 值可能为（）

A、0 B、 $\frac{π}{12}$ C、 $\frac{π}{6}$ D、 $\frac{π}{3}$

查看试题解析
10. 已知四棱锥 $P - A B C D$ 的底面ABCD为梯形， $A B ∥ D C$ ， $∠ B A D = 90 °$ ， $A D = C D = 2$ ， $A B = 4$ ， $△ P A B$ 为正三角形，平面 $P A B ⊥$ 平面ABCD，E，F分别为PA，PB的中点，则（）

A、 $C F$ $∥$ 平面PAD B、PD与平面ABCD所成角的正弦值为 $\frac{\sqrt{5}}{5}$ C、 $D E ⊥ P B$ D、四棱锥 $P - A B C D$ 的体积为 $8 \sqrt{3}$

查看试题解析
11. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ ， $F_{1}$ ， $F_{2}$ 为 $C$ 的左、右焦点， $B (0 ， 4 b)$ ，直线 $B F_{2}$ 与 $C$ 的一支交于点 $P$ ，且 $\frac{| B P |}{| P F_{2} |} = λ (λ \geq 1)$ ，则 $C$ 的离心率最大值为（）

A、 $\sqrt{5}$ B、2 C、 $2 \sqrt{2}$ D、 $2 \sqrt{5}$

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} x + 2 ， x < 0 \\ {(x - 1)}^{2} ， x \geq 0 \end{array}$ ，函数 $y = t$ 的图象与曲线 $y = f (x)$ 有3个不同的交点，其横坐标依次为 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ，设 $x_{1} < x_{2} < x_{3}$ ，则 $x_{2} - x_{1} x_{3}$ 的取值范围为（）

A、 $[2 ， \frac{86}{27}]$ B、 $(2 ， \frac{86}{27}]$ C、 $(2 ， 3]$ D、 $[2 ， 3]$

查看试题解析

二、填空题

13. 已知向量 $\vec{a} = (x + 1 ， \sqrt{3})$ ， $\vec{b} = (1 ， 0)$ ， $\vec{a} \cdot \vec{b} = - 2$ ，则向量 $\vec{a} + \vec{b}$ 与 $\vec{b}$ 的夹角为．

查看试题解析
14. 2022年11月29日，神舟十五号载人飞船成功发射升空，在飞船入轨后未来6个月里，空间站将逐步解锁、安装并测试15个科学实验机柜，开展涵盖空间科学研究与应用、航天医学、航天技术等领域的40余项空间科学实验和技术试验．已知此科学实验机柜在投入使用前会进行调试工作，现有8个科学实验机柜，其中包括5个A类型、3个B类型，两名调试员计划共抽取3个机柜进行调试，则至少有1人抽到B类型机柜进行调试的概率为．

查看试题解析
15. 已知正项数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，满足 $4 S_{n} = a_{n}^{2} + 2 a_{n} - 8$ ，则 $a_{8} =$ ．

查看试题解析
16. 在正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A B = A D = 2$ ， $A A_{1} = 4$ ， M，N在棱 $B B_{1}$ ， $D D_{1}$ 上，且 $B_{1} M = 2$ ， $D_{1} N = 1$ ，过 $A_{1} M N$ 的平面交 $C C_{1}$ 于G，则截面 $A_{1} M G N$ 的面积为；若线段 $A_{1} G$ 上存在一点P，使得 $A P ⊥ A_{1} G$ ，则 $\frac{P G}{A_{1} G} =$ ．

查看试题解析

三、解答题

17. 已知锐角 $△ A B C$ 的内角A，B，C的对边分别为a，b，c．在下列三个条件① $\vec{m} = (s i n A ， - \frac{\sqrt{3}}{2})$ ， $\vec{n} = (2 c o s 2 A ， 2 c o s A)$ ，且 $\vec{m} / / \vec{n}$ ；② $a s i n B = \sqrt{3} b c o s A$ ；③ $c o s^{2} B + c o s^{2} C = c o s^{2} A + 1 - s i n B s i n C$ 中任选一个，回答下列问题．

(1)、求A；

(2)、若 $a = 2$ ，求 $△ A B C$ 面积的最大值．

查看试题解析
18. 在三棱锥 $S - A B C$ 中，底面ABC是边长为4的正三角形，侧面 $S A C ⊥$ 底面ABC， $S A = S C$ ， $S B = 2 \sqrt{5}$ ，点E在线段SB上，且 $\frac{S E}{E B} = \frac{2}{3}$ ．

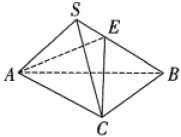(1)、证明： $S B ⊥$ 平面ACE；

(2)、求二面角 $A - S B - C$ 的正弦值．

查看试题解析
19. 锚定2060碳中和，中国能源演进“绿之道”，为响应绿色低碳发展的号召，某地在沙漠治理过程中，计划在沙漠试点区域四周种植红柳和梭梭树用于防风固沙，中间种植适合当地环境的特色经济作物，通过大量实验发现，单株经济作物幼苗的成活率为0.8，红柳幼苗和梭梭树幼苗成活的概率均为p，且已知任取三种幼苗各一株，其中至少有两株幼苗成活的概率不超过0.896．
附：若随机变量Z服从正态分布 $N (μ ， σ^{2})$ ，则 $P (μ - σ ≤ Z ≤ μ + σ) \approx 0.6827$ ， $P (μ - 2 σ ≤ Z ≤ μ + 2 σ) \approx 0.9545$ ， $P (μ - 3 σ \leq Z \leq μ + 3 σ) \approx 0.9973$ ．

(1)、当p最大时，经济作物幼苗的成活率也将提升至0.88，求此时三种幼苗均成活的概率（ $\sqrt{10.24} = 3.2$ ）；

(2)、正常情况下梭梭树幼苗栽种5年后，其树杆地径服从正态分布 $N (250 ， 5^{2})$ （单位：mm）．
㈠梭梭树幼苗栽种5年后，若任意抽取一棵梭梭树，则树杆地径小于235mm的概率约为多少？（精确到0.001）
㈡为更好地监管梭梭树的生长情况，梭梭树幼苗栽种5年后，农林管理员随机抽取了10棵梭梭树，测得其树杆地径均小于235mm，农林管理员根据抽检结果，认为该地块土质对梭梭树的生长产生影响，计划整改地块并选择合适的肥料，试判断该农林管理员的判断是否合理？并说明理由．

查看试题解析
20. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ， A，B为其左、右顶点，M为椭圆上一点，且 $k_{M A} \cdot k_{M B} = - \frac{3}{4}$ ．

(1)、求C的离心率；

(2)、若左焦点 $F_{1}$ 到椭圆上的点的最大距离为3，且直线 $M F_{2}$ 交C于另一点N，已知 $△ A M F_{2}$ 的面积是 $△ A N F_{2}$ 的2倍，求直线MN的方程．

查看试题解析
21. 已知函数 $f (x) = a l n x - x^{2}$ ．

(1)、讨论 $f (x)$ 的单调性；

(2)、若函数 $g (x) = f (x) + (2 - a) x$ 恰有两个零点，求实数a的取值范围．

查看试题解析
22. 在直角坐标系xOy中，曲线 $C_{1}$ 的参数方程为 ${\begin{array}{l} x = t + 4 \\ y = \sqrt{16 - t^{2}} \end{array}$ （t为参数），曲线 $C_{2}$ 的参数方程为 ${\begin{array}{l} x = - \frac{1}{2} s \\ y = 8 \sqrt{3} + \frac{\sqrt{3}}{2} s \end{array}$ （s为参数）．

(1)、求曲线 $C_{2}$ 被曲线 $C_{1}$ 所截得的弦长；

(2)、以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线 $C_{3}$ 的极坐标方程为 $ρ c o s θ + \sqrt{3} ρ s i n θ - 8 = 0$ ，记曲线 $C_{1}$ 与 $C_{3}$ 交于A，B两点，求 $\vec{O A} \cdot \vec{O B}$ ．

查看试题解析
23. 已知函数 $f (x) = | 3 x - 2 | + | 3 x + a | (a \in R)$ ．

(1)、当 $a = 2$ 时，求不等式 $f (x) \leq 6$ 的解集；

(2)、若 $f (x) \geq 4$ ，求a的取值范围．

查看试题解析