四川省德阳市2023届高三理数下学期4月三诊考试试卷
试卷更新日期:2023-05-10 类型:高考模拟
一、单选题
-
1. 在复平面内,复数(i是虚数单位)对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知集合 , 则( )A、 B、 C、 D、3. 已知互相垂直的平面α,β交于直线l,若直线m,n满足m∥α,n⊥β,则( )A、m∥l B、m∥n C、n⊥l D、m⊥n4. 已知 , q:任意 , 则p是q成立的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件5. 经济学家在研究供求关系时,一般用纵轴表示产品价格(自变量),而用横轴来表示产品数量(因变量).某类产品的市场供求关系在不受外界因素(如政府限制最高价格等)的影响下,市场会自发调解供求关系:当产品价格低于均衡价格时,需求量大于供应量,价格会上升为;当产品价格高于均衡价格时,供应量大于需求量,价格又会下降,价格如此波动下去,产品价格将会逐渐靠近均衡价格 . 能正确表示上述供求关系的图形是( ).A、
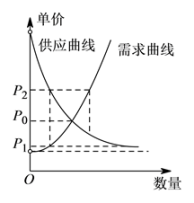 B、
B、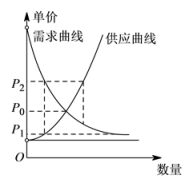 C、
C、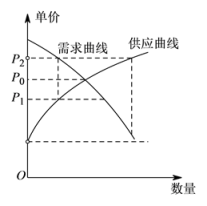 D、
D、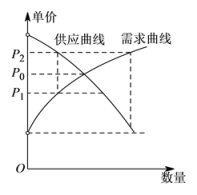 6. 已知矩形ABCD的面积为8,当矩形ABCD周长最小时,沿对角线AC把折起,则三棱锥D-ABC的外接球表面积等于( )A、 B、 C、 D、不确定的实数7. 函数()的部分图象如图所示,其中两点之间的距离为5,则的递增区间是( )
6. 已知矩形ABCD的面积为8,当矩形ABCD周长最小时,沿对角线AC把折起,则三棱锥D-ABC的外接球表面积等于( )A、 B、 C、 D、不确定的实数7. 函数()的部分图象如图所示,其中两点之间的距离为5,则的递增区间是( )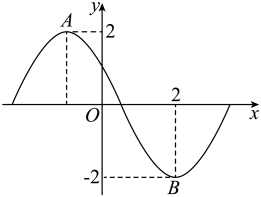 A、 B、 C、 D、8. 设x,y满足约束条件则的最大值是( )A、-3 B、-6 C、-7 D、129. 已知D为正三角形ABC中边BC的中点,E在线段AC上且 , 若AD与BE交于M,若 , 则正三角形ABC的边长为( )A、6 B、12 C、18 D、2410. 唐代诗人李颀的诗《古从军行》开头两句是“白日登山望烽火,黄昏饮马傍交河”.诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为 , 若将军从点处出发,河岸线对应的直线方程为x+y=2,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”问题中的最短总路程为( )A、6 B、5 C、4 D、311. 已知实数x、y满足 , 则x、y的大小关系为( )A、 B、 C、 D、12. 已知、为椭圆与双曲线的公共焦点,P是其一个公共点, , 则椭圆与双曲线离心率之积的最小值为( )A、 B、1 C、 D、2
A、 B、 C、 D、8. 设x,y满足约束条件则的最大值是( )A、-3 B、-6 C、-7 D、129. 已知D为正三角形ABC中边BC的中点,E在线段AC上且 , 若AD与BE交于M,若 , 则正三角形ABC的边长为( )A、6 B、12 C、18 D、2410. 唐代诗人李颀的诗《古从军行》开头两句是“白日登山望烽火,黄昏饮马傍交河”.诗中隐含着一个有趣的数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为 , 若将军从点处出发,河岸线对应的直线方程为x+y=2,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”问题中的最短总路程为( )A、6 B、5 C、4 D、311. 已知实数x、y满足 , 则x、y的大小关系为( )A、 B、 C、 D、12. 已知、为椭圆与双曲线的公共焦点,P是其一个公共点, , 则椭圆与双曲线离心率之积的最小值为( )A、 B、1 C、 D、2二、填空题
-
13. 已知的展开式中x的系数为2,则实数a的值为 .14. 设抛物线 的焦点为 ,经过点 的直线 与抛物线相交于 , 两点,又知点 恰为 的中点,则15. 已知的外接圆O的半径为1, . 从圆O内随机取一点M,若点M在内的概率恰为 , 则的周长为 .16. 如图所示,一个正四棱锥和一个正三棱锥所有棱长都相等,F为棱的中点,将和 , 和 , 和分别对应重合为P,B,C得到一个组合体.关于该组合体有如下三个结论:①AD⊥SP;②直线AD与直线SF所成角为60°;③ . 其中正确结论的个数是 .

三、解答题
-
17. 已知数列是等差数列,且满足 , . 数列的前n项和是 , 且 .(1)、求数列及数列的通项公式;(2)、若 , 求数列的前n项和 .18. 某学校高二年级某学科的教师决定帮助本年级100名对该科学习困难的学生.为了做到精准帮助,教师对这100名学生的学习兴趣、学习态度、学习习惯等进行调查,并把调查结果转化为各学生的学困指标x,将指标x分成 , , , , 五组,得到如图所示的频率分布直方图.规定若 , 则认定该生为“绝对学困生”,否则认定该生为“相对学困生”;当时,认定该生为“亟待帮助生”.
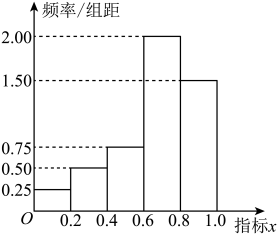 (1)、分别求出“绝对学困生”,“亟待帮助生”的人数;并求学困指标的平均值.(2)、在学困指标处于内的学困生中,随机选取两名,用X表示所选两名学生中“亟待帮助生”的人数,求X的分布列和数学期望.19. 如图,在中, , P为AB边上一动点,交AC于点D,现将沿PD翻折至 .
(1)、分别求出“绝对学困生”,“亟待帮助生”的人数;并求学困指标的平均值.(2)、在学困指标处于内的学困生中,随机选取两名,用X表示所选两名学生中“亟待帮助生”的人数,求X的分布列和数学期望.19. 如图,在中, , P为AB边上一动点,交AC于点D,现将沿PD翻折至 .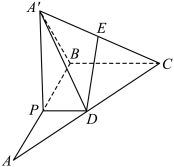 (1)、沿PD翻折中是否会改变二面角的大小,并说明理由;(2)、若PB=CB=2PD=2,E是的中点.求证:平面 , 并求当平面平面PBCD时,二面角的余弦值.20. 已知椭圆:的离心率为 , 、分别是其左、右焦点,若是椭圆上的右顶点,且 .(1)、求椭圆的方程;(2)、设直线与椭圆交于两点,点关于轴的对称点为(与不重合),问直线与轴是否交于一个定点?若是,请写出该定点的坐标,并证明你的结论;若不是,请说明理由.
(1)、沿PD翻折中是否会改变二面角的大小,并说明理由;(2)、若PB=CB=2PD=2,E是的中点.求证:平面 , 并求当平面平面PBCD时,二面角的余弦值.20. 已知椭圆:的离心率为 , 、分别是其左、右焦点,若是椭圆上的右顶点,且 .(1)、求椭圆的方程;(2)、设直线与椭圆交于两点,点关于轴的对称点为(与不重合),问直线与轴是否交于一个定点?若是,请写出该定点的坐标,并证明你的结论;若不是,请说明理由.