2022-2023学年初数北师大版八年级下册第六章平行四边形全章测试卷

试卷更新日期：2023-05-10 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 下列条件中，不能判断四边形ABCD是平行四边形的是（）

A、AB=CD，AD∥BC B、∠A=∠C，∠A+∠B=180° C、AD=BC，AD∥BC D、∠A=∠C，∠B=∠D

查看试题解析
2. 在四边形ABCD中，AB∥CD且AB=CD，若∠B=56°，则∠C的度数是（）

A、56° B、65° C、114° D、124°

查看试题解析
3. 如图，四边形ABCD是平行四边形，∠BAC=90°，BD=10，AC=6，则AB的长为（）

A、4 B、5 C、6 D、8

查看试题解析
4. 如图，四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 交于点 $O$ ，下列条件不能判定四边形 $A B C D$ 为平行四边形的是（）

A、 $∠ B A D = ∠ B C D$ ， $∠ A B C = ∠ A D C$ B、 $∠ A B C = ∠ A D C$ ， $A B / / C D$ C、 $A B / / C D$ ， $O B = O D$ D、 $A B = C D$ ， $O A = O C$

查看试题解析
5. 如图，将平行四边形ABCD沿对角线AC折叠，使点B落在点B'处，若∠1=48°，∠2=32°，则∠B的度数为（）

A、124° B、114° C、104° D、56°

查看试题解析
6. 如图，在 $▱$ ABCD中，∠ABC的平分线交AD于E，AE=3，DE=2，则 $▱$ ABCD的周长为（）

A、11 B、12 C、16 D、22

查看试题解析
7. 一个多边形每个内角都是150°，这个多边形是（）

A、九边形 B、十边形 C、十二边形 D、十八形

查看试题解析
8. 如图，为测量位于一水塘旁的两点A，B间的距离，在地面上确定点O，分别取OA，OB的中点C，D，量得CD=10m，则A，B之间的距离是（）

A、10 m B、20 m C、5 m D、40 m

查看试题解析
9. 如图，在四边形ABCD中，点P是对角线BD的中点，点E、F分别是AB、CD的中点，AD=BC，∠CBD=30°，∠ADB=100°，则∠PFE的度数是（）

A、15° B、25° C、30° D、35°

查看试题解析
10. 如图，P为平行四边形ABCD内一点，过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点，若S_四边形_AHPE＝3，S_四边形_PFCG＝5，则S_△_PBD为（）

A、0.5 B、1 C、1.5 D、2

查看试题解析

二、填空题（每空3分，共24分）

11. 如图，在 $▱ A B C D$ 中， $A E ⊥ C D$ 于点E，若 $∠ B = 55 °$ ，则 $∠ D A E$ 的度数为．

查看试题解析
12. 如图，在△ABC中，点D，E分别是AB，AC的中点，连结BE，若AE＝6，DE＝5，∠BEC＝90°，则BE＝.

查看试题解析
13. 一个n边形的内角和等于外角和的2倍，则n=

查看试题解析
14. 如图，将一副三角板在平行四边形 $A B C D$ 中作如下摆放，设 $∠ 1 = 30 °$ ，那么 $∠ 2 =$ .

查看试题解析
15. 如图，平行四边形ABCD，点F是BC上的一点，∠FAD=60°，AE平分∠FAD，交CD于点E，且点E是CD的中点，连接EF，已知AD=5，CF=3，则EF=

查看试题解析
16. 一个多边形的内角和跟它的外角和相等，则这个多边形是边形．

查看试题解析
17. 如图，在平行四边形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O，在 $D C$ 的延长线上取点E，使 $C E = \frac{1}{2} C D$ ，连接 $O E$ 交 $B C$ 于点F，若 $B C = 12$ ，则 $C F =$ ．

查看试题解析
18. 如图，在平面直角坐标系中， $▱ A O B C$ 的顶点B在x轴上，点A坐标为 $(1 ， 2)$ ，以点O为圆心，任意长为半径画弧，分别交OA，OB于点D，E，再分别以点D，点E为圆心，以大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧在∠AOB内相交于点F，作射线OF交AC于点P．则点P的坐标是．

查看试题解析

三、解答题（共7题，共66分）

19. 作图：

(1)、直接写出AC的长为 .

(2)、在图1中找到格点D，画出以点A、B、C、D为顶点的平行四边形，画出所有的情况的平行四边形.

(3)、在图2中找到格点D，画出以点A、B、C、D为顶点且周长最小的平行四边形，直接写出周长最小值.

(4)、在（3）条件下，直接写出平行四边形的面积.

查看试题解析
20. 如图，在 $△ A B C$ 中，D、E分别为AB、AC的中点，过点C作 $C F / / B D$ 交DE的延长线于点F．

(1)、求证：四边形BCFD为平行四边形；

(2)、若 $B C = 6$ ，求EF的长．

查看试题解析
21. 如图，四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点 $O$ ， $A O = C O$ ， $E F$ 过点 $O$ 且与 $A D$ 、 $B C$ 分别相交于点 $E$ 、 $F$ ， $O E = O F$

(1)、求证：四边形 $A B C D$ 是平行四边形；

(2)、连接 $A F$ ，若 $E F ⊥ A C$ ， $Δ A B F$ 周长是15，求四边形 $A B C D$ 的周长.

查看试题解析
22. 已知：如图，在△ABC中，M、N分别是边AB、AC的中点，D是边BC延长线上的一点，且 $C D = \frac{1}{2} B C$ ，联结CM、DN.

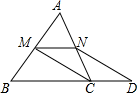(1)、求证：四边形MCDN是平行四边形；

(2)、若三角形AMN的面积等于5，求梯形MBDN的面积.

查看试题解析
23. 如图，在▱ABCD中，点E在边AD上，连接EB并延长至F，使BF＝BE；连接EC并延长至G，使CG＝CE，连接FG，点H为FG的中点，连接DH，AF．

(1)、若∠BAE＝70°，∠DCE＝20°，求∠DEC的度数；

(2)、求证：四边形AFHD为平行四边形．

查看试题解析
24. 如图，在四边形ABCD中，AB $∥$ CD，∠ABC=∠ADC，DE垂直于对角线AC，垂足是E，连接BE．

(1)、求证：四边形ABCD是平行四边形；

(2)、若点E是AC的中点，判断BE与AC的位置关系，并说明理由；

(3)、若△ABE是等边三角形，AD= $\sqrt{14}$ ，求对角线AC的长．

查看试题解析
25. 如图，在 $▱ A B C D$ 中， $A B = B D$ ，点 $E$ 在射线 $B D$ 上（不与 $B$ ， $D$ 重合）， $C F ∥ A E$ 交直线 $B D$ 于点 $F$ ．

(1)、如图1，当点 $E$ 在线段 $B D$ 上时，请直接写出 $B E$ ， $B F$ ， $C D$ 之间的数量关系；

(2)、如图2，当点 $E$ 在线段 $B D$ 的延长线上时，请写出 $B E$ ， $B F$ ， $C D$ 之间的数量关系，并加以证明．

查看试题解析

2022-2023学年初数北师大版八年级下册第六章 平行四边形 全章测试卷

一、单选题（每题3分，共30分）

二、填空题（每空3分，共24分）

三、解答题（共7题，共66分）

2022-2023学年初数北师大版八年级下册第六章平行四边形全章测试卷