2022-2023学年初数北师大版八年级下册6.4 多边形的内角与外角和 同步训练必刷题
试卷更新日期：2023-05-10 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 五边形的外角和为（ ）A、180° B、360° C、450° D、540°2. 正多边形的每一个外角都等于45°，则这个多边形的边数是（ ）A、6 B、7 C、8 D、93. 在五边形ABCDE中，∠A，∠B，∠C，∠D，∠E的度数之比为3：5：3：4：3，则∠D的外角等于（ ）A、60° B、75° C、90° D、120°4. 若一个正多边形的每一个外角都等于36°，则这个正多边形的边数是（ ）A、7 B、8 C、9 D、105. 如图，五边形ABCDE是正五边形，F，G是边CD，DE上的点，且BF∥AG．若∠CFB=57°，则∠AGD=（ ）
A、108° B、36° C、129° D、72°6. 一个多边形的每个内角均为120°，则这个多边形是（ ）A、五边形 B、六边形 C、七边形 D、八边形．7. 一个多边形的内角和是外角和的4倍，这个多边形的边数是（ ）A、8 B、9 C、10 D、118. 若n边形的内角和与外角和相加为 ， 则n的值为（ ）A、7 B、8 C、9 D、109. 衢州钟灵塔的塔基是个正n边形（n是正整数）.测得塔基所在的正n边形的一个外角为60°，如图所示，n的值是（ ）
A、5 B、6 C、7 D、810. 如图，五边形ABCDE中， ， ， 、、分别是、、的外角，则等于（ ）
A、 B、 C、 D、二、填空题（每空3分，共30分）
-
11. 七边形的内角和为度.12. 一个多边形的内角和是其外角和的4倍，则这个多边形的边数是.13. 如图所示的多边形中，根据标出的各内角度数，求出x的值是 ．
14. 如图，在四边形ABCD中，∠A+∠C=136°，点E在边AD上，连结BE，若∠D与∠EBC互补，则∠EBA的值为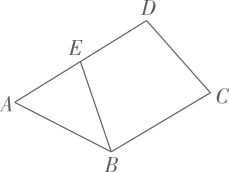
15. 第五套人民币中的5角硬币色泽为镍白色，正，反面的内周边缘均为正十一边形.则其内角和为 °.
16. 如果一个多边形的每个外角都是 ， 那么这个多边形的边数为 ．17. 已知一个多边形的内角和再加上一个外角共 ， 则这个多边形的边数是18. 在平行四边形中，：：：：：： ， 则.19. 足球表面为什么用正六边形和正五边形构成？因为正六边形的两个内角和正五边形的一个内角加起来接近一个周角，而又不足一个周角．这样，由平面折叠而成的多面体充气后最终就呈现为球形．如图，在折叠前的平面上，拼接点处的缝隙∠AOB的大小为 ．
20. 如图，点A、B、C、D、E在同一平面内，连接、、、、 ， 若 ， 则 ．
三、解答题（共6题，共60分）
-
21. 多边形上或内部的一点与多边形各顶点的连线，可以将多边形分割成若干个小三角形.如图，给出了四边形的三种具体分割方法，分别将四边形分割成了2个、3个、4个小三角形，这样我们就可以借助研究三角形的经验研究四边形了.
图①被分割成2个小三角形
图②被分割成3个小三角形
图③被分割成4个小三角形
(1)、请按照上述三种方法分别将图中的六边形进行分割，并写出每种方法所得到的小三角形的个数：
图①被分割成个小三角形、图②被分割成个小三角形、图③被分割成个小三角形；
(2)、如果按照上述三种分割方法分别分割 边形，请写出每种方法所得到的小三角形的个数(用含 的代数式写出结论即可，不必画图)：按照上述图①、图②、图③的分割方法， 边形分别可以被分割成、、个小三角形.22. 已知一个多边形的内角和与外角和之比为11：2。(1)、求这个多边形的内角和；(2)、求这个多边形的边数。23. 在四边形ABCD中，∠A=140°，∠D=80°
(1)、如图1，若∠B=∠C，试求出∠C的度数；(2)、如图2，若∠ABC的平分线BE交DC于点E，且BE∥AD，试求出∠C的度数；(3)、如图3，若∠ABC和∠BCD的平分线相交于点E，试求出∠BEC的度数。24. 如图
(1)、如图1，求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数；(2)、如图2，求∠1+∠2+∠3+∠4+∠5+∠6的度数。
