2022-2023学年初数北师大版八年级下册6.3 三角形的中位线同步训练必刷题
试卷更新日期:2023-05-10 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图,在 中,点D,点E分别是边AB,AC的中点,若 ,则DE-( )
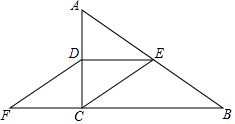
 A、1 B、2 C、3 D、42. 如图,在△ABC中,D、E分别为AB、AC的中点,CF平分∠ACB,交DE于点F,若AC=4,则EF的长为( )
A、1 B、2 C、3 D、42. 如图,在△ABC中,D、E分别为AB、AC的中点,CF平分∠ACB,交DE于点F,若AC=4,则EF的长为( ) A、1 B、2 C、3 D、43. 已知:中,D、E、F分别是边、、的中点,则四边形的周长等于( )
A、1 B、2 C、3 D、43. 已知:中,D、E、F分别是边、、的中点,则四边形的周长等于( ) A、 B、 C、 D、的周长4. 如图,A,B两地被池塘隔开,小明通过下面的方法估测出了A,B间的距离:先在外选一点C,然后步测出 , 的中点M,N,并步测出的长为12米,由此他就知道A,B间的距离是( )
A、 B、 C、 D、的周长4. 如图,A,B两地被池塘隔开,小明通过下面的方法估测出了A,B间的距离:先在外选一点C,然后步测出 , 的中点M,N,并步测出的长为12米,由此他就知道A,B间的距离是( ) A、6米 B、12米 C、24米 D、48米5. 如图,中, , 则的值为( )
A、6米 B、12米 C、24米 D、48米5. 如图,中, , 则的值为( ) A、6 B、 C、7 D、86. 如图所示,▱ABCD中,对角线AC,BD交于点O,E是CD中点,连接OE,若OE=3cm,则AD的长为( )
A、6 B、 C、7 D、86. 如图所示,▱ABCD中,对角线AC,BD交于点O,E是CD中点,连接OE,若OE=3cm,则AD的长为( ) A、3cm B、6cm C、9cm D、12cm7. 如图,矩形ABCD的对角线AC,BD交于点O,点E,F分别为AO,AD的中点,若EF=4,AB=8,则∠ACB的度数为( )
A、3cm B、6cm C、9cm D、12cm7. 如图,矩形ABCD的对角线AC,BD交于点O,点E,F分别为AO,AD的中点,若EF=4,AB=8,则∠ACB的度数为( ) A、30° B、35° C、45° D、60°8. 如图,▱的对角线 , 交于点 , 是的中点,连结 , , , 若 , 则等于( )
A、30° B、35° C、45° D、60°8. 如图,▱的对角线 , 交于点 , 是的中点,连结 , , , 若 , 则等于( ) A、3 B、4 C、5 D、69. 如图,矩形ABCD中,AB=2,BC=3,P是CD边的中点,E是BC边上的一动点,M、N分别是AE、PE的中点,随着点E的运动,线段MN长( )
A、3 B、4 C、5 D、69. 如图,矩形ABCD中,AB=2,BC=3,P是CD边的中点,E是BC边上的一动点,M、N分别是AE、PE的中点,随着点E的运动,线段MN长( ) A、不断增大 B、先增大,后减小 C、保持不变,长度为 D、保持不变,长度为10. 如图,将△ABC沿着它的中位线DE对折,点A落在F处.若∠C=120°,∠A=20°,则∠FEB的度数是( )
A、不断增大 B、先增大,后减小 C、保持不变,长度为 D、保持不变,长度为10. 如图,将△ABC沿着它的中位线DE对折,点A落在F处.若∠C=120°,∠A=20°,则∠FEB的度数是( ) A、140° B、120° C、100° D、80°
A、140° B、120° C、100° D、80°二、填空题(每空3分,共30分)
-
11. 如图,在平行四边形中, , 点E,F分别是 , 的中点,则的长为 .
 12. 如图,在中, , , 分别是 , , 的中点,若的周长是12,则的周长是 .
12. 如图,在中, , , 分别是 , , 的中点,若的周长是12,则的周长是 . 13. 如图,在中, , , , 点D在外,连接、 , 点E是的中点, , , 则线段的长 .
13. 如图,在中, , , , 点D在外,连接、 , 点E是的中点, , , 则线段的长 . 14. 东东家有一块等腰三角形的空地ABC,如图,已知E,F分别是边AB,AC的中点,量得AB=AC=12米,BC=10米,他想把四边形BCFE用篱笆围成一圈养鸡,则需篱笆长米.
14. 东东家有一块等腰三角形的空地ABC,如图,已知E,F分别是边AB,AC的中点,量得AB=AC=12米,BC=10米,他想把四边形BCFE用篱笆围成一圈养鸡,则需篱笆长米. 15. 如图,在矩形中, , , 为边的中点,点在线段上运动,是的中点,则的周长的最小值是.
15. 如图,在矩形中, , , 为边的中点,点在线段上运动,是的中点,则的周长的最小值是. 16. 如图,的对角线AC,BD相交于点O,点E是AD的中点,连接OE,若 , 的周长为5,则的周长等于 .
16. 如图,的对角线AC,BD相交于点O,点E是AD的中点,连接OE,若 , 的周长为5,则的周长等于 . 17. 如图,人字梯保险杠两端点D,E分别是梯柱AB,AC的中点,梯子打开时DE=38cm,此时梯脚的距离BC长为 cm.
17. 如图,人字梯保险杠两端点D,E分别是梯柱AB,AC的中点,梯子打开时DE=38cm,此时梯脚的距离BC长为 cm. 18.
18.
如图, , 分别为矩形的边 , 的中点,连接 , , .已知 , , 则的长为.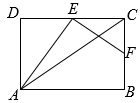 19. 如图,已知矩形ABCD的两条边AB=6,AD=8,点E是对角线AC、BD的交点,点P是边AD上一个动点,作点D关于直线PE的对称点D′,当ED′与矩形一条边垂直时,PD的长是 .
19. 如图,已知矩形ABCD的两条边AB=6,AD=8,点E是对角线AC、BD的交点,点P是边AD上一个动点,作点D关于直线PE的对称点D′,当ED′与矩形一条边垂直时,PD的长是 . 20. 如图, , , , 分别是四边形边 , , , 的中点,若 , 则四边形的周长为 .
20. 如图, , , , 分别是四边形边 , , , 的中点,若 , 则四边形的周长为 .
三、解答题(共6题,共60分)
-
21. 如图所示,在△ABC中,D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF//BC.
 (1)、求证:四边形BDEF是平行四边形.(2)、线段BF,AB,AC的数量之间具有怎样的关系?证明你所得到的结论.22. 如图,四边形ABCD为平行四边形,E为AD上的一点,连结EB并延长至点F,使BF=BE,连结EC并延长至点G,使CG=CE,连结FG.H为FG的中点,连结DH,AF。
(1)、求证:四边形BDEF是平行四边形.(2)、线段BF,AB,AC的数量之间具有怎样的关系?证明你所得到的结论.22. 如图,四边形ABCD为平行四边形,E为AD上的一点,连结EB并延长至点F,使BF=BE,连结EC并延长至点G,使CG=CE,连结FG.H为FG的中点,连结DH,AF。 (1)、求证:四边形AFHD为平行四边形;(2)、若CB=CE,∠EBC=75°,∠DCE=10°,求∠DAB的度数。23. 如图,在△ABC中,中线BD,CE相交于点O,F,G分别是OB,OC的中点。
(1)、求证:四边形AFHD为平行四边形;(2)、若CB=CE,∠EBC=75°,∠DCE=10°,求∠DAB的度数。23. 如图,在△ABC中,中线BD,CE相交于点O,F,G分别是OB,OC的中点。 (1)、求证:四边形DEFG是平行四边形;(2)、连结AO,若BC=7,AO=5,则平行四边形DEFG的周长为。24. 如图,在△ABC中,AD平分∠BAC,AD⊥BD于点D,取BC的中点E,连结DE。
(1)、求证:四边形DEFG是平行四边形;(2)、连结AO,若BC=7,AO=5,则平行四边形DEFG的周长为。24. 如图,在△ABC中,AD平分∠BAC,AD⊥BD于点D,取BC的中点E,连结DE。 (1)、求证:DE∥AC;(2)、若AB=8,AC=12,求DE的长。
(1)、求证:DE∥AC;(2)、若AB=8,AC=12,求DE的长。