人教版七年级下数学期末复习知识点扫盲满分计划——5.1相交线
试卷更新日期:2023-05-10 类型:复习试卷
一、相交线:对顶角相等,邻补角互补
-
1. 如图,直线AB与直线CD相交于点O,若∠AOC增大40°,则∠BOD( )
 A、减少40° B、增大40° C、不变 D、增大0°2. 如图,直线、相交于点O, , . 则 .
A、减少40° B、增大40° C、不变 D、增大0°2. 如图,直线、相交于点O, , . 则 . 3. 如图,点O在直线AB上,∠COE是直角,OF平分∠AOE,∠COF=30°,求∠EOB的大小.
3. 如图,点O在直线AB上,∠COE是直角,OF平分∠AOE,∠COF=30°,求∠EOB的大小.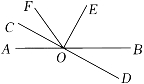 4. 如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOC的度数是( )
4. 如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOC=110°,则∠BOC的度数是( ) A、115° B、125° C、135° D、145°5. 如图,直线AB、CD、EF相交于点O,若∠1+∠2=150°,则∠3=°.
A、115° B、125° C、135° D、145°5. 如图,直线AB、CD、EF相交于点O,若∠1+∠2=150°,则∠3=°.
二、垂线:垂线段最短;距离必须为垂线段
-
6. 如图,已知AB⊥BC,垂足为B,AB=3,点P是射线BC上的动点,则线段AP长不可能是( )
 A、5 B、4 C、3 D、2.57. 如图,污水处理厂要从A处把处理过的水引入排水沟PQ,做法如下:过点A作AB⊥PQ于点B,沿着AB方向铺设排水管道可用料最省.能准确解释这一现象的数学知识是( )
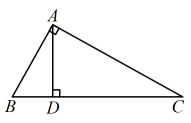
A、5 B、4 C、3 D、2.57. 如图,污水处理厂要从A处把处理过的水引入排水沟PQ,做法如下:过点A作AB⊥PQ于点B,沿着AB方向铺设排水管道可用料最省.能准确解释这一现象的数学知识是( ) A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、过直线外一点有且只有一条直线与这条直线平行8. 如图所示, , , 下列说法错误的是( )
A、两点之间线段最短 B、两点确定一条直线 C、垂线段最短 D、过直线外一点有且只有一条直线与这条直线平行8. 如图所示, , , 下列说法错误的是( ) A、点B到AC的垂线段是线段AB B、点C到AB的垂线段是线段AC C、线段AD是点D到BC的垂线段 D、线段BD是点B到AD的垂线段9. 如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
A、点B到AC的垂线段是线段AB B、点C到AB的垂线段是线段AC C、线段AD是点D到BC的垂线段 D、线段BD是点B到AD的垂线段9. 如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( ) A、垂线段最短 B、点到直线的距离 C、两点确定一条直线 D、两点之间线段最短10. 在下列图形中,线段的长表示点P到直线的距离的是( )A、
A、垂线段最短 B、点到直线的距离 C、两点确定一条直线 D、两点之间线段最短10. 在下列图形中,线段的长表示点P到直线的距离的是( )A、 B、
B、 C、
C、 D、
D、
三、同位角、内错角、同旁内角:公共边为截线
-
11. 如图所示,∠1和∠2是同位角的是( )
 A、②③ B、①②③ C、①②④ D、①④12. 如下图,直线AD、BE被直线BF和AC所截,下列说法正确的是( )
A、②③ B、①②③ C、①②④ D、①④12. 如下图,直线AD、BE被直线BF和AC所截,下列说法正确的是( ) A、∠3与∠4是同旁内角 B、∠2与∠5是同位角 C、∠6与∠1是内错角 D、∠2与∠6是同旁内角13. 如图所示,在所标识的角中,内错角是( )
A、∠3与∠4是同旁内角 B、∠2与∠5是同位角 C、∠6与∠1是内错角 D、∠2与∠6是同旁内角13. 如图所示,在所标识的角中,内错角是( )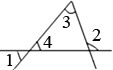 A、和 B、和 C、和 D、和14. 如图,直线a、b被直线c所截,则与是内错角.
A、和 B、和 C、和 D、和14. 如图,直线a、b被直线c所截,则与是内错角. 15. 如图,下列各组角中,互为内错角的是( )
15. 如图,下列各组角中,互为内错角的是( ) A、和 B、和 C、和 D、和
A、和 B、和 C、和 D、和四、综合训练
-
16. 如图,直线AB,CD相交于点O,OF⊥OC于O,OE平分∠AOF,∠COE=15°,求∠BOD的度数.
 17. 如图,直线AB,CD相交于点O,OE⊥AB.若∠DOE=2∠AOC,则∠BOD的度数为( )
17. 如图,直线AB,CD相交于点O,OE⊥AB.若∠DOE=2∠AOC,则∠BOD的度数为( ) A、25° B、30° C、60° D、75°18. 如图,直线 , 相交于点 , , 垂足为O,且平分.若 , 求的大小.
A、25° B、30° C、60° D、75°18. 如图,直线 , 相交于点 , , 垂足为O,且平分.若 , 求的大小.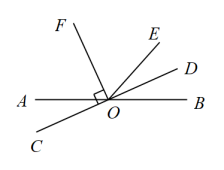 19. 如图,直线和相交于点O,平分 , .若 , , 则以下等式一定成立的是( )
19. 如图,直线和相交于点O,平分 , .若 , , 则以下等式一定成立的是( )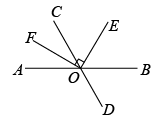 A、 B、 C、 D、20. 如图,三角尺的直角顶点P在直线上,点A,B在直线的同侧.
A、 B、 C、 D、20. 如图,三角尺的直角顶点P在直线上,点A,B在直线的同侧. (1)、如图①,若 , 求的度数.(2)、如图②,若平分 , 平分 , 求的度数.(3)、绕点P旋转三角尺 , 使点A,B在直线的异侧,如图③,当时,求的度数.21. 如图,射线的方向是北偏东 , 射线的方向是北偏西 , 是的角平分线.是的反向延长线.求:
(1)、如图①,若 , 求的度数.(2)、如图②,若平分 , 平分 , 求的度数.(3)、绕点P旋转三角尺 , 使点A,B在直线的异侧,如图③,当时,求的度数.21. 如图,射线的方向是北偏东 , 射线的方向是北偏西 , 是的角平分线.是的反向延长线.求: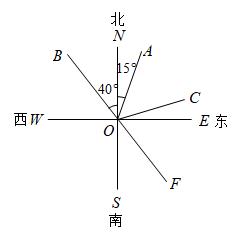 (1)、射线的方向.(2)、的度数.22. 下列四个说法:①两点确定一条直线;②过直线上一点有且只有一条直线垂直于已知直线;③连接直线外一点与直线上各点的所有线段中,垂线段最短;④从直线外一点到这条直线的垂线段,叫做点到直线的距离,其中正确的说法的个数是( )A、1 B、2 C、3 D、423. 已知点O是直线AB上一点,过O作射线OC,使∠BOC=110°.
(1)、射线的方向.(2)、的度数.22. 下列四个说法:①两点确定一条直线;②过直线上一点有且只有一条直线垂直于已知直线;③连接直线外一点与直线上各点的所有线段中,垂线段最短;④从直线外一点到这条直线的垂线段,叫做点到直线的距离,其中正确的说法的个数是( )A、1 B、2 C、3 D、423. 已知点O是直线AB上一点,过O作射线OC,使∠BOC=110°. (1)、如图①,∠AOC=;(2)、如图②,过点O作射线OD使∠COD=90°,作∠AOC的平分线OE,求∠DOE的度数;(3)、在(2)的条件下,作射线OF,若∠BOF与∠AOE互余,画出图形,并求出∠DOF的度数.24. 如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=25°,求∠COD的度数.
(1)、如图①,∠AOC=;(2)、如图②,过点O作射线OD使∠COD=90°,作∠AOC的平分线OE,求∠DOE的度数;(3)、在(2)的条件下,作射线OF,若∠BOF与∠AOE互余,画出图形,并求出∠DOF的度数.24. 如图,直线AB与直线MN相交,交点为O,OC⊥AB,OA平分∠MOD,若∠BON=25°,求∠COD的度数. 25. 过点向边作垂线段,下列画法中正确的是( )A、
25. 过点向边作垂线段,下列画法中正确的是( )A、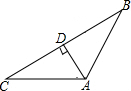 B、
B、 C、
C、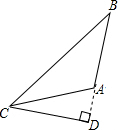 D、
D、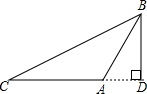 26. 如图,在所标注的角中.
26. 如图,在所标注的角中. (1)、对顶角有对,邻补角有对;(2)、若 , , 求与的度数.27. 如图所示,点C到AB所在的直线的距离是指图中线段( )的长度.
(1)、对顶角有对,邻补角有对;(2)、若 , , 求与的度数.27. 如图所示,点C到AB所在的直线的距离是指图中线段( )的长度.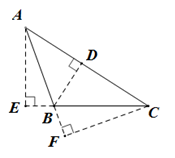 A、AE B、CF C、BD D、BE28. 如图,直线EF和CD相交于点O,射线 , 且OC平分∠AOF,∠BOD=20°.求∠BOE的度数.
A、AE B、CF C、BD D、BE28. 如图,直线EF和CD相交于点O,射线 , 且OC平分∠AOF,∠BOD=20°.求∠BOE的度数. 29. 如图,点C到直线的距离是( )
29. 如图,点C到直线的距离是( ) A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度
A、线段的长度 B、线段的长度 C、线段的长度 D、线段的长度