广西邕衡金卷2023届高三理数一轮复习诊断性联考试卷
试卷更新日期:2023-05-09 类型:高考模拟
一、单选题
-
1. 若 , 则( )A、 B、 C、 D、2. 关于统计数据的分析,有以下几个结论,其中正确的是( )A、将一组数据中的每个数据都减去同一个数后,平均数与方差均没有变化 B、样本数据9、3、5、7、12、13、1、8、10、18的中位数是8或9 C、在刻画回归模型的拟合效果时,相关指数的值越大,说明拟合的效果越好 D、在调查影院中观众观后感时,从20排中(每排人数相同)每排任意抽取一人进行调查是系统抽样法3. 已知集合 , , 则( )A、 B、 C、 D、4. 某几何体的三视图如图所示,则该几何体的体积为( )
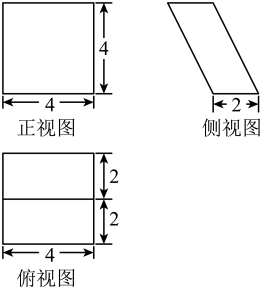 A、 B、8 C、32 D、5. 函数的图象大致为( )A、
A、 B、8 C、32 D、5. 函数的图象大致为( )A、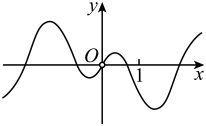 B、
B、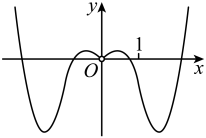 C、
C、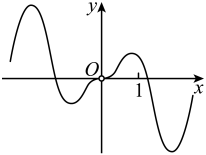 D、
D、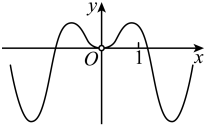 6. 已知函数 , 且 , 在区间上有最小值,则的取值范围为( )A、 B、 C、 D、7. 如图,在直三棱柱中,棱长均为 . , , 分别为 , , 的中点,则直线与平面所成角的正弦值是( )
6. 已知函数 , 且 , 在区间上有最小值,则的取值范围为( )A、 B、 C、 D、7. 如图,在直三棱柱中,棱长均为 . , , 分别为 , , 的中点,则直线与平面所成角的正弦值是( )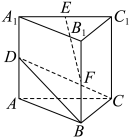 A、 B、 C、 D、8. 如图,在扇形中,C是弦的中点,D在上, . 其中 , 长为 . 则的长度约为(提示:时,)( )
A、 B、 C、 D、8. 如图,在扇形中,C是弦的中点,D在上, . 其中 , 长为 . 则的长度约为(提示:时,)( )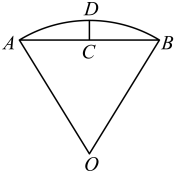 A、 B、 C、 D、9. 如图,圆锥的轴截面为正三角形,点为顶点,点为底面圆心,过轴的三等分点(靠近点)作平行底面的截面,以该截面为底面挖去一个圆柱,此圆柱的下底面在圆锥的底面上,则所得圆柱的体积与原圆锥的体积之比为( )
A、 B、 C、 D、9. 如图,圆锥的轴截面为正三角形,点为顶点,点为底面圆心,过轴的三等分点(靠近点)作平行底面的截面,以该截面为底面挖去一个圆柱,此圆柱的下底面在圆锥的底面上,则所得圆柱的体积与原圆锥的体积之比为( )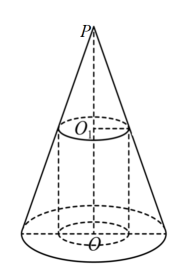 A、1:9 B、2:9 C、1:27 D、2:2710. 设函数在区间恰有三个极值点、三个零点,则的取值范围是( )A、 B、 C、 D、11. 已知双曲线 , 左焦点为 , 虚轴上端点为 , 直线与双曲线交于 , 两点,直线与直线的倾斜角互补,且点满足 , 双曲线的离心率为 , 则( )A、 B、 C、 D、12. 设 , , , 则( )A、 B、 C、 D、
A、1:9 B、2:9 C、1:27 D、2:2710. 设函数在区间恰有三个极值点、三个零点,则的取值范围是( )A、 B、 C、 D、11. 已知双曲线 , 左焦点为 , 虚轴上端点为 , 直线与双曲线交于 , 两点,直线与直线的倾斜角互补,且点满足 , 双曲线的离心率为 , 则( )A、 B、 C、 D、12. 设 , , , 则( )A、 B、 C、 D、二、填空题
-
13. 已知 , 与的夹角 , 则在方向上的投影为.14. 现有6个乒乓球,其中3个是新球3个是旧球,不放回地抽取两次,每次取一个球,则在第一次取到新球的条件下,第二次取到旧球的概率是 .15. 设为椭圆的两个焦点,为上关于坐标原点对称的两点,且 , 则四边形的面积为 .16. 在中, , 点在线段上,且 , , 则面积的最大值为 .
三、解答题
-
17. 记为数列的前项和.已知 .(1)、证明:是等比数列;(2)、记 , 求前项和的最小值.18. 已知四棱锥中,底面为直角梯形,平面 , , , , , M为中点,过C,D,M的平面截四棱锥所得的截面为 .
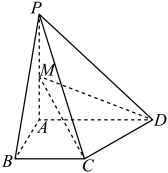 (1)、若与棱交于点F,画出截面 , 保留作图痕迹(不用说明理由),求点F的位置;(2)、求平面与平面所成锐二面角的余弦值.19. 为了丰富学生的课外活动,学校举办篮球、足球、羽毛球比赛,经过前期的预赛和半决赛,最终甲、乙两个班级进入决赛,决赛中每个项目胜方得8分,负方得0分,没有平局.三个项目比赛结束后,总得分高的班级获得冠军.已知甲班级在篮球、足球、羽毛球中获胜的概率分别为0.4,0.8,0.6,各项目的比赛结果相互独立.(1)、求甲班级获得冠军的概率;(2)、用X表示乙班级的总得分,求X的分布列与期望.20. 设抛物线的焦点为 , 点 , 过的直线交于 , 两点.当直线垂直于轴时, .(1)、求的方程;(2)、若点 , , 过点A的动直线交抛物线于、 , 直线交抛物线于另一点 , 连接并延长交抛物线于点S.证明直线与直线的斜率之和为定值.
(1)、若与棱交于点F,画出截面 , 保留作图痕迹(不用说明理由),求点F的位置;(2)、求平面与平面所成锐二面角的余弦值.19. 为了丰富学生的课外活动,学校举办篮球、足球、羽毛球比赛,经过前期的预赛和半决赛,最终甲、乙两个班级进入决赛,决赛中每个项目胜方得8分,负方得0分,没有平局.三个项目比赛结束后,总得分高的班级获得冠军.已知甲班级在篮球、足球、羽毛球中获胜的概率分别为0.4,0.8,0.6,各项目的比赛结果相互独立.(1)、求甲班级获得冠军的概率;(2)、用X表示乙班级的总得分,求X的分布列与期望.20. 设抛物线的焦点为 , 点 , 过的直线交于 , 两点.当直线垂直于轴时, .(1)、求的方程;(2)、若点 , , 过点A的动直线交抛物线于、 , 直线交抛物线于另一点 , 连接并延长交抛物线于点S.证明直线与直线的斜率之和为定值.