安徽省蚌埠市五河县2023届数学二模试卷
试卷更新日期:2023-05-09 类型:高考模拟
一、单选题
-
1. 对于数集 , , 定义 , , , 若集合 , 则集合中所有元素之和为( )A、 B、 C、 D、2. 复数 =( )A、 B、 C、 D、3. ( )A、 B、 C、 D、4. 若直线 与曲线 有两个不同的交点,则实数 的取值范围是( )A、 B、 C、 D、5. 已知某地区中小学生人数如图①所示,为了解该地区中小学生的近视情况,卫生部门根据当地中小学生人数,用分层抽样的方法抽取了10%的学生进行调查,调查数据如图②所示,则估计该地区中小学生的平均近视率为( )
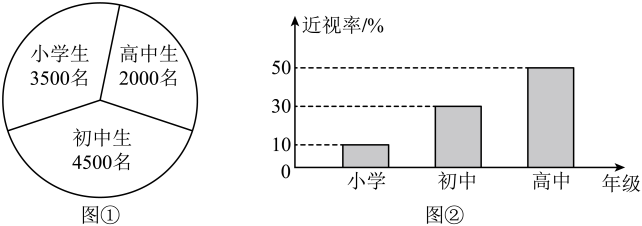 A、50% B、32% C、30% D、27%6. 已知椭圆的右焦点为 , 上顶点为 , 若直线与圆:相切,则该椭圆的离心率为( )A、 B、 C、 D、或7. 函数 的图象如图所示,则下列结论成立的是( )
A、50% B、32% C、30% D、27%6. 已知椭圆的右焦点为 , 上顶点为 , 若直线与圆:相切,则该椭圆的离心率为( )A、 B、 C、 D、或7. 函数 的图象如图所示,则下列结论成立的是( )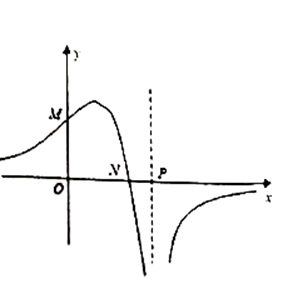 A、 B、 C、 D、8. 在△ABC中,已知 ,且 ,角A是锐角,则△ABC的形状是( )A、直角三角形 B、等腰三角形 C、等腰直角三角形 D、等边三角形
A、 B、 C、 D、8. 在△ABC中,已知 ,且 ,角A是锐角,则△ABC的形状是( )A、直角三角形 B、等腰三角形 C、等腰直角三角形 D、等边三角形二、多选题
-
9. 数列共有项(常数为大于5的正整数),对任意正整数 , 有 , 且当时,.记的前项和为 , 则下列说法中正确的有( )A、若 , 则 B、中可能出现连续五项构成等差数列 C、对任意小于的正整数 , 存在正整数 , 使得 D、对中任意一项 , 必存在 , 使得按照一定顺序排列可以构成等差数列10. 已知过抛物线的焦点的直线与抛物线交于点、 , 若、两点在准线上的射影分别为、 , 线段的中点为 , 则下列叙述正确的是( )A、 B、四边形的面积等于 C、 D、直线AC与抛物线相交11. 如图,在棱长为的正方体中,为线段上一动点(包括端点),则以下结论正确的有( )
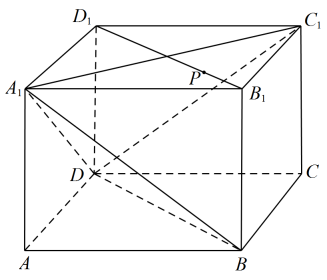 A、三棱锥外接球表面积为 B、三棱锥的体积为定值 C、过点平行于平面的平面被正方体截得的多边形的面积为 D、直线与平面所成角的正弦值的范围为12. 已知函数 , 则下列说法中正确的是( )A、函数的图象关于原点对称 B、函数的图象关于轴对称 C、函数在上是减函数 D、函数的值域为
A、三棱锥外接球表面积为 B、三棱锥的体积为定值 C、过点平行于平面的平面被正方体截得的多边形的面积为 D、直线与平面所成角的正弦值的范围为12. 已知函数 , 则下列说法中正确的是( )A、函数的图象关于原点对称 B、函数的图象关于轴对称 C、函数在上是减函数 D、函数的值域为三、填空题
-
13. 设 , 向量 , , , 且 , , 则= .14. 的展开式中含的项的系数是 .15. 若直线过点 , 则的最小值为 .16. 已知为奇函数,当时,;则当 , 的解析式为.
四、解答题
-
17. 某地有一家知名蛋糕房根据以往某种蛋糕在天里的销售记录,绘制了以下频数分布表:
日销售量单位:个
频数
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)、求在未来连续天里,有连续天的日销量都不低于个且另一天的日销售量低于个的概率;(2)、用表示在未来天里日销售量不低于个的天数,求随机变量的概率分布、均值和方差 .18. △的内角A,B,C的对边分别为a,b,c,已知.(1)、求角C;(2)、若 , 求的面积.19. 已知等比数列的前项和为 , 且 , , 成等差数列.(1)、求的值及数列的通项公式;(2)、若求数列的前项和20. 如图,已知四棱锥的底面是菱形,平面平面 , 为的中点,点在上,.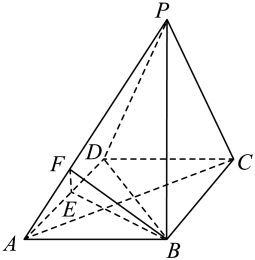 (1)、证明:平面;(2)、若 , 且与平面所成的角为 , 求平面与平面夹角的余弦值.
(1)、证明:平面;(2)、若 , 且与平面所成的角为 , 求平面与平面夹角的余弦值.