浙江省温州市三校联盟2022-2023学年七年级下学期期中数学试题
试卷更新日期：2023-05-09 类型：期中考试
一、选择题(每小题3分，共30分)
-
1. 下列大学校微可以看成是由图案自身的一部分经平移后得到的为（ ）A、
B、
C、
D、
2. 科学家在实验中测出某微生物细胞的直径约为0.0000035米，将0.0000035用科学记计数法表示为（ ）A、3.5×10-6 B、3.5×10-5 C、35×10-5 D、3.5×1063. 下列各式是二元一次方程的是（ ）A、y=x-1 B、x+=2 C、x+y-3 D、x+xy=84. 如图，平行线AB，CD被直线AE所截，∠1=80°，则∠2的度数是（ ）
A、80° B、90° C、100° D、110°5. 若(x-5)(x+4)=x2+ax-20，则a的值为（ ）A、-5 B、-1 C、1 D、46. 下列计算中正确的是（ ）A、a2+a3=a5 B、a2·a3=a6 C、a6÷a2=a4 D、(2a)3=6a37. 如果是关于x、y的二元一次方程ax+y=1的解，那么a的值为（ ）A、-2 B、-1 C、0 D、I8. 小温同学在美术课上将△ABC通过平移设计得到“一棵树”，已知底边AB上的高CD为5cm，沿CD方向向下平移3cm到△A1B1C1的位置，再经过相同的平移到△A2B2C2的位置，下方树干EF长为6cm，则树的高度CF长为（ ）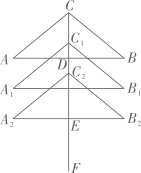
A、19 B、17 C、15 D、119. 《九章算术》是我国传统数学的重要著作，其中记载了一个数学问题：今有共买物，人出八，盈三；人出七，不足四，问物价为几何？译文：今有人合伙购物，每人出8钱，会多出3钱：每人出7钱，又会差4钱．问物价是多少？设共有x人，物价为y钱，根据题意得（ ）A、 B、 C、 D、10. 已知M，N分别是长方形纸条ABCD边AB，CD上两点(AM>DN)，如图1所示，沿M，N所在直线进行第一次折叠，点A，D的对应点分别为点E，F，EM交CD于点P；如图2所示，继续沿PM进行第二次折叠，点B，C的对应点分别为点G，H，若∠1=∠2．则∠CPM的度数为（ ）
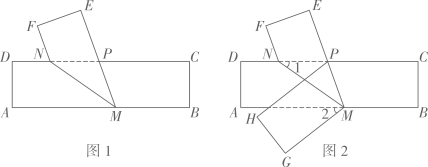A、74° B、72° C、70° D、68°二、 填空题(每小题3分， 共24分)
-
11. 2x·(-5xy)= ．12. 已知2x+y=8，用含x的代数式表示y，则y= ．13. 如图，要使AD∥BC只需添加一个条件，这个条件是 ． (填一个正确的即可，不添加其它字母与辅助线)
14. 计算(-5)4×()4=15. 已知直线m∥n，将一块含30°角的直角三角板ABC按如图方式放置(∠ABC=30°)，直线m交AB，AC于点D，E，点B落在直线n上，若∠1=25°，则∠2的度数为.
16. 定义一种新运算： a★b=ab-a2 ， 则x★(x+y)= ．17. 已知关于x，y的二元一次方程组 ， 则代数式-2x-2y的值为 ．18. 如图1，有甲，乙两种大小不同的正方形纸片，把正方形甲放置在正方形乙中，连结EO，FO，得到图2，再将图2这样的四个图案不重叠，无缝隙地拼成如图3所示的正方形ABCD，若正方形ABCD的阴影区域面积和为12，且FM=4，则一张正方形甲和一张正方形乙的面积和为
三、解答题(本题有6小题，共46分)
-
19.(1)、计算：(-4)0+(-1)2023+()-1(2)、化简： (-8x2+16x)÷(4x)．20. 解方程组：(1)、(2)、21. 先化简，再求值；(x+ 1)2+(3+x)(3-x)，其中x=-2．22. 如图是10×8的正方形网格，每个小正方形的边长为1，其顶点称为格点．请按要求在图中画出格点三角形(顶点均在格点上) ．
(1)、平移格点三角形ABC， 画出平移后的格点三角形EFG(点A，B，C的对应点分别为点E，F，G)，使点D落在线段EF上(2)、三角形EFG的面积为 ．23. 如图，在三角形ABE中，C，D，F分别是三边上的点，BC∥FD，∠1+∠2=180°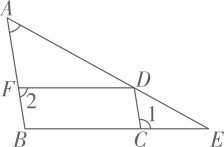
(1)、判断AB与CD的位置关系，并说明理由：(2)、若∠A=60°，∠1=4∠ADF，求∠ADF的度数．24. 根据以下素材，探索完成任务。设计烟花采购方案
自疫情开放以来，旅游业逐步回暖，为吸引游客，温州某乡镇决定举办烟花节，需考虑如何采购烟花及烟花燃放时长．
素材1
已知购买20箱A型和10箱B型烟花需要5500元，购买30箱A型和20箱B型烟花需要9500元．
素材2
某烟花厂提供产品信息如下：
(1)A型烟花每箱12发，B型烟花每箱20发．
(2)即将推出新品C型烟花，每箱200元，每箱20发．
(3)本厂生产的所有型号烟花每发间隔5秒．
素材3
(1)该乡镇准备支出9000元(全部用完)购买烟花．
(2)燃放烟花时逐箱不间断燃放，且每次仅燃放一箱，假设每发烟花均能正常绽放，且间隔时长保持不变，忽略每箱烟花之间的引燃时间，
问题解决
任务1
确定单价
求A，B型烟花每箱多少元？
任务2
确定方案①
若仅购买A， B型烟花，可以燃放多少秒？
确定方案②
若同时采购A，B，C三种烟花，A型烟花的箱数是C型的4倍，如何采购使得燃放时间最长？并求出最长燃放时间。