浙江省湖州市长兴县2022-2023学年八年级下学期4月期中数学试题

试卷更新日期：2023-05-09 类型：期中考试

进入出卷网下载

一、选择题(每小题3分，共30分)

1. 二次根式 $\sqrt{32}$ 的化简结果正确的是（）

A、 $2 \sqrt{4}$ B、 $2 \sqrt{8}$ C、 $4 \sqrt{2}$ D、 $8 \sqrt{2}$

查看试题解析
2. 下列方程中，没有实数根的是（）

A、x²-2x+1=0 B、x²-2x+5=0 C、x²-2x-1=0 D、x²-2x-2=0．

查看试题解析
3. 在3，2，1，3，2，2，4，5这八个数据中，众数是（）

A、2 B、3 C、4 D、5

查看试题解析
4. 十二边形的外角和的度数为（）

A、 $180 °$ B、 $360 °$ C、 $720 °$ D、 $1800 °$

查看试题解析
5. 如图，在 $▱$ ABCD中，下列说法一定正确的是（）

A、AB=AD B、AO=BO C、OC=OD D、AD=BC

查看试题解析
6. 如图， $▱$ ABCD的对角线AC与BD相交于点O，AB⊥AC，若AB=4，BO=5，则AC的长是（）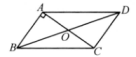

A、3 B、5 C、6 D、8

查看试题解析
7. 在同一平面内，设a，b，c是三条互相平行的直线，已知a与b间的距离为5 cm，b与c间的距离为4 cm，则a与c间的距离为（）cm．

A、1 B、9 C、4或5 D、1或9

查看试题解析
8. 在八年级数学运算比赛中，A班荣获团体总分第一名．A班参赛选手比赛成绩的方差计算公式为：S²= $\frac{1}{6}$ [(x₁-38)²+(x₂-38)²+……+(x₆-38)²]，下列说法错误的是（）

A、A班一共派出了6名选手 B、A班参赛选手的平均成绩为38分 C、A班选手比赛成绩的中位数为38 D、A班选手比赛成绩的团体总分为228分

查看试题解析
9. 已知y= $\sqrt{x - 5}$ + $\sqrt{5 - x}$ +2，则x^y（）

A、-10 B、7 C、10 D、25

查看试题解析
10. 已知实数x，y满足(x²+y²-1)²+x²+y²-3=0，则x²+y²的值是（）

A、1或-2 B、-1或2 C、2 D、1

查看试题解析

二、填空题(每小题4分，共24分)

11. 计算： $\sqrt{14} \div \sqrt{2}$ = ．

查看试题解析
12. 某研究员要对甲．乙两种植株进行考察，分别随机选取相同数量的两种植株后，对它们的高度进行测量并计算出了高度的方差分别为 $S_{甲}^{2}$ =2.4， $S_{乙}^{2}$ =3.6．从以上信息可知，这两种植株中，比较整齐的是植株．

查看试题解析
13. 一个n边形，它的内角和等于它的外角和，则n= ．

查看试题解析
14. 已知x=a是方程x²-3x-5=0的根，代数式2a²-6a+4的值为．

查看试题解析
15. 如图，直线AE∥BD，点C在BD上．若BD=9，△ABD的面积为27，△ACE的面积为18，则AE= ．

查看试题解析
16. 如图四边形ABCD，AD∥BC，AB⊥BC，AD=3，AB=6，BC=9，P为AB边上的一动点，以PD，PC为边作平行四边形PCQD，则对角线PQ的长的最小值是．

查看试题解析

三、解答题：(共66分)

17. 计算：

(1)、 $\sqrt{12} \times \sqrt{\frac{4}{3}}$ ；

(2)、 $（ \sqrt{3} - \sqrt{2} ）^{2}$

查看试题解析
18. 解下列方程：

(1)、4x²-3x=0；

(2)、x²-8x-1=0．

查看试题解析
19. 如图，在 $▱$ ABCD中，点E，F分别是AD，BC上的点，且DE=BF，连结BE，DF．
求证：BE=DF．

查看试题解析
20. 高空抛物极其危险，是我们必须杜绝的行为.据研究，高空抛出的物体下落的时间t（单位：s）和高度h（单位：m）近似满足 $t = \sqrt{\frac{h}{5}}$ （不考虑风速的影响）.

(1)、从200m高空抛物到落地所需时间t是多少？

(2)、从高空抛物经过3s落地，该物体下落的高度是多少？

查看试题解析

21. 某校举办了一次趣味数学比赛，满分100分，学生得分均为整数，这次比赛中，甲、乙两组学生成绩如下(单位：分)

甲组：30 ，60， 60， 60， 60， 60，70， 90，90， 100

乙组：50， 60， 60， 60，70，70，70，70，80 ，90．

组别	平均数	中位数	方差
甲组	68	a	376
乙组	b	70

(1)、以上成绩统计分析表中a=分，b=分

(2)、小亮同学说：“这次比赛我得了70分，在我们小组中属中游略偏上！”观察上面表格判断，小亮可能是甲、乙哪个组的学生？并说明理由．

(3)、计算乙组成绩的方差，如果你是该校数学比赛的教练员，现在需要你选一组同学代表学校参加复赛，你会选择哪一组？并说明理由．

查看试题解析

22. 如图，在4X4的正方形网格中，每个小正方形的边长为1，请在所给网格中按下列要求画出图形，

(1)、已知点A在格点(即小正方形的顶点)上，画一个平行四边形ABCD，使AB= $\sqrt{10}$ ， BC= $\sqrt{5}$ ，且点A，B，C，D都在格点上(只需画出符合条件的一个平行四边形)；

(2)、所画出的平行四边形ABCD的边AB上的高线长为多少？

查看试题解析
23. 某工厂生产并销售A，B两种型号车床共14台，生产并销售1台A型车床可以获利10万元；如果生产并销售不超过4台B型车床，则每台B型车床可以获利17万元，如果超出4台B型车床，则每超出1台，每台B型车床获利将均减少1万元．

(1)、请分别计算生产并销售A型车床5台与11台时，工厂的总获利分别是多少？

(2)、若生产并销售B型车床比生产并销售A型车床获得的利润多70万元，问：生产并销售B型车床多少台？

查看试题解析
24. 如图，平行四边形ABCD的对角线AC，BD交于点O，AE平分∠BAD，交BC于点E，且∠ADC= 60°．

(1)、求证：AE=BE；

(2)、若 $\frac{B C}{A B}$ =n(n>1)，AC= $4 \sqrt{3}$ ，连结OE；
①若n=2，求平行四边形ABCD的周长；

②若四边形OECD的面积是△OAD面积的k倍，请用含k的代数式表示n．

查看试题解析