湖北省武汉市洪山区2022-2023学年七年级下学期期中数学试卷
试卷更新日期:2023-05-09 类型:期中考试
一、单选题
-
1. 每年的5月8日是世界微笑日,在对别人的微笑中,你也会看到世界对自己微笑起来.下列图案是由图中所示的图案平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在实数:3.14159, , 1.010010001, , , 中,是无理数的有( )A、1个 B、2个 C、3个 D、4个3. 已知点 , 则点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,直线交于点O, , 把分为两部分,且 , 则的度数为( )
2. 在实数:3.14159, , 1.010010001, , , 中,是无理数的有( )A、1个 B、2个 C、3个 D、4个3. 已知点 , 则点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 如图,直线交于点O, , 把分为两部分,且 , 则的度数为( ) A、120° B、140° C、108° D、126°5. 如图,下列说法错误的是( )
A、120° B、140° C、108° D、126°5. 如图,下列说法错误的是( ) A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以6. 关于“”,下列说法不正确的是( )A、它可以表示面积为10的正方形的边长 B、若 , 则整数 C、 D、数轴上距离原点个单位长度的点有且只有一个7. 如图,将5个大小相同的长方形置于平面直角坐标系中,若顶点 , , 则顶点的坐标是( )
A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以6. 关于“”,下列说法不正确的是( )A、它可以表示面积为10的正方形的边长 B、若 , 则整数 C、 D、数轴上距离原点个单位长度的点有且只有一个7. 如图,将5个大小相同的长方形置于平面直角坐标系中,若顶点 , , 则顶点的坐标是( ) A、 B、 C、 D、8. 下列命题中,是真命题的为( )A、两条直线被第三条直线所截,内错角相等 B、直线外一点与直线上所有点的连线段中,垂线段最短 C、过一点有且只有一条直线与已知直线垂直 D、垂直于同一直线的两直线平行9. 如图, , 点P在射线上.分别平分 , , 若 , 且 , 则的度数为( )
A、 B、 C、 D、8. 下列命题中,是真命题的为( )A、两条直线被第三条直线所截,内错角相等 B、直线外一点与直线上所有点的连线段中,垂线段最短 C、过一点有且只有一条直线与已知直线垂直 D、垂直于同一直线的两直线平行9. 如图, , 点P在射线上.分别平分 , , 若 , 且 , 则的度数为( ) A、 B、 C、 D、10. “幻方”最早记载于春秋时期的《大戴礼记》中,如图1所示,每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等,现将填入如图2所示的“幻方”中,部分数据已填入,则的值为( )
A、 B、 C、 D、10. “幻方”最早记载于春秋时期的《大戴礼记》中,如图1所示,每个三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等,现将填入如图2所示的“幻方”中,部分数据已填入,则的值为( ) A、512 B、64 C、128 D、−512
A、512 B、64 C、128 D、−512二、填空题
-
11. 计算: = .12. 已知点 , , 则线段的长为.13. 如图,在三角形ABC中, , , 将三角形沿着与垂直的方向向上平移3cm得到三角形 , 则线段与扫过的面积之和为.
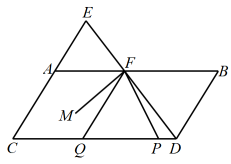
 14. 若的整数部分为 , 的小数部分为 , 则 .15. 如果点的坐标满足 , 那么称点P为和谐点.若和谐点P到y轴的距离为3,则点P的坐标为.16. 如图,点E在的延长线上,与交于点F,且 , , , P为线段上一动点,Q为上一点,且满足 , 为的平分线.下列结论:
14. 若的整数部分为 , 的小数部分为 , 则 .15. 如果点的坐标满足 , 那么称点P为和谐点.若和谐点P到y轴的距离为3,则点P的坐标为.16. 如图,点E在的延长线上,与交于点F,且 , , , P为线段上一动点,Q为上一点,且满足 , 为的平分线.下列结论:①;②平分;③;④.
其中结论正确的有(填写所有正确结论的序号).
三、解答题
-
17.(1)、计算:;(2)、解方程:.18. 完成下面推理过程:
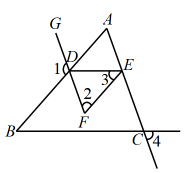
如图,点G,D,F共线,且 , , 求证:.
证明:∵ , (已知),
∴( ),
∴( ).
∴( ).
∵ ,
∴( ).
∴( ).
∴( ).
∵( ).
∴( ).
19. 小明同学用两个小正方形纸片做拼剪构造大正方形的游戏:(他选用的两个小正方形的面积分别为 , ). (1)、如图1, , , 拼成的大正方形边长为;
(1)、如图1, , , 拼成的大正方形边长为;如图2, , , 拼成的大正方形边长为;
如图3, , , 拼成的大正方形边长为.
(2)、若将(1)中的图3沿正方形边的方向剪裁,能否剪出一个面积为24且长宽之比为的长方形?若能,求它的长和宽;若不能,请说明理由.20. 如图,将一个长方形纸片沿所在直线折叠,使得点C,D的对应点分别为点N,M,NF交于点G,过点G作 , 交于点H. (1)、若 , 求的度数;(2)、求证:平分.21. 如图是由小正方形组成的9×9网格,每个小正方形的顶点叫做格点,每个小正方形的边长为1个单位长度.的顶点都是格点,将向左平移1格,再向上平移3格;
(1)、若 , 求的度数;(2)、求证:平分.21. 如图是由小正方形组成的9×9网格,每个小正方形的顶点叫做格点,每个小正方形的边长为1个单位长度.的顶点都是格点,将向左平移1格,再向上平移3格; (1)、在图中作出平移后的(2)、连接 , , 则这两条线段的关系是;(3)、过点A作射线 , 将分成两个面积相等的两个三角形,交于点N;(4)、找出格点E(不与B重合),使得与面积相等(只需找一个点E即可).22. 一个长方形台球桌面如图1所示,已知台球在与台球桌边缘碰撞的过程中,撞击线路与桌边的夹角等于反弹线路与桌边的夹角,即图1中的.
(1)、在图中作出平移后的(2)、连接 , , 则这两条线段的关系是;(3)、过点A作射线 , 将分成两个面积相等的两个三角形,交于点N;(4)、找出格点E(不与B重合),使得与面积相等(只需找一个点E即可).22. 一个长方形台球桌面如图1所示,已知台球在与台球桌边缘碰撞的过程中,撞击线路与桌边的夹角等于反弹线路与桌边的夹角,即图1中的. (1)、台球经过如图2所示的两次碰撞后,第二次的反弹线路为.若开始时的撞击线路为 , 求证:;(2)、台球桌因为长期使用,导致桌角松动变形如图3,在台球经过两次撞击之后,开始时的撞击线路EF所在直线与第二次的反弹线路所在直线相交于点M,若 , 求的度数.23. 如图,已知直线.
(1)、台球经过如图2所示的两次碰撞后,第二次的反弹线路为.若开始时的撞击线路为 , 求证:;(2)、台球桌因为长期使用,导致桌角松动变形如图3,在台球经过两次撞击之后,开始时的撞击线路EF所在直线与第二次的反弹线路所在直线相交于点M,若 , 求的度数.23. 如图,已知直线. (1)、在图1中,点E在直线上,点F在直线上,点G在之间,若 , , 则;(2)、如图2,若平分 , 延长交于点M,且 , 当时,求的度数;(3)、在(2)的条件下,若绕E点以每秒转动4°的速度逆时针旋转一周,同时绕F点以每秒转动1°的速度逆时针旋转,当转动结束时也随即停止转动,在整个转动过程中,当秒时,.24. 在平面直角坐标系中,点 , 的坐标满足: , 将线段向右平移到的位置(点A与D对应,点B与C对应).
(1)、在图1中,点E在直线上,点F在直线上,点G在之间,若 , , 则;(2)、如图2,若平分 , 延长交于点M,且 , 当时,求的度数;(3)、在(2)的条件下,若绕E点以每秒转动4°的速度逆时针旋转一周,同时绕F点以每秒转动1°的速度逆时针旋转,当转动结束时也随即停止转动,在整个转动过程中,当秒时,.24. 在平面直角坐标系中,点 , 的坐标满足: , 将线段向右平移到的位置(点A与D对应,点B与C对应). (1)、直接写出点A的坐标 , 点B的坐标;(2)、如图1,将线段向右平移3个单位得到线段 , 求四边形的面积;(3)、如图2,点是四边形所在平面内的一点,且三角形的面积为4,求m,n之间的数量关系.
(1)、直接写出点A的坐标 , 点B的坐标;(2)、如图1,将线段向右平移3个单位得到线段 , 求四边形的面积;(3)、如图2,点是四边形所在平面内的一点,且三角形的面积为4,求m,n之间的数量关系.