湖北省武汉市洪山区2022-2023学年八年级下学期期中数学试卷
试卷更新日期:2023-05-09 类型:期中考试
一、单选题
-
1. 若二次根式在实数范围内有意义,则n的取值范围是( )A、 B、 C、 D、2. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 下列条件中,能够判断△ABC为直角三角形的是( )A、 , , B、 C、 D、5. 在下列给出的条件中,不能判定四边形ABCD为平行四边形的是( )A、 B、 C、 , D、6. 如图,某天下午2时,两艘船只分别从港口O点处出发,其中快船沿北偏东方向以2海里/时的速度行驶,慢船沿北偏西方向以1海里/时的速度行驶,当天下午4时,两艘船只分别到达A,B两点,则此时两船之间的距离等于( )
 A、海里 B、海里 C、2海里 D、2海里7. 顺次连接四边形四边中点所得的四边形一定是( )A、平行四边形 B、矩形 C、菱形 D、正方形8. 等腰中, , 若 , 则的长度为( )A、 B、或 C、 D、或9. 如图,将菱形的边以直线为对称轴翻折至 , 使点C恰好落在上.若此时 , 则的度数为( )
A、海里 B、海里 C、2海里 D、2海里7. 顺次连接四边形四边中点所得的四边形一定是( )A、平行四边形 B、矩形 C、菱形 D、正方形8. 等腰中, , 若 , 则的长度为( )A、 B、或 C、 D、或9. 如图,将菱形的边以直线为对称轴翻折至 , 使点C恰好落在上.若此时 , 则的度数为( ) A、 B、 C、 D、10. 如图,菱形的对角线长度为4,边长 , M为菱形外一个动点,满足 , N为中点,连接.则当M运动的过程中,长度的最大值为( )
A、 B、 C、 D、10. 如图,菱形的对角线长度为4,边长 , M为菱形外一个动点,满足 , N为中点,连接.则当M运动的过程中,长度的最大值为( ) A、 B、 C、1 D、2
A、 B、 C、1 D、2二、填空题
-
11. 化简二次根式:=.12. 如图,在数轴上表示1的点为A,以为边构造正方形 , 以O为圆心,为半径画圆弧交数轴于点D,则D点表示的数为.
 13. 如图,在中,D,E,F分别是 , , 的中点,若 , , 则的周长为.
13. 如图,在中,D,E,F分别是 , , 的中点,若 , , 则的周长为. 14. 如图,菱形的内角 , 以为边向外作等腰直角 , 连接交于F,则.
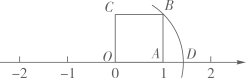
14. 如图,菱形的内角 , 以为边向外作等腰直角 , 连接交于F,则.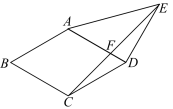 15. 已知 , 为的高且 , N为中点,则的长度为.16. 如图1所示,一个三角形纸片的尺寸为: , 将其放置于图2所示的矩形纸板上,首先移动到的位置,接着又移动到的位置,其中点A,B, , 均位于矩形纸板的边上.若在两次移动过程中,恰有 , 则线段的长度等于.
15. 已知 , 为的高且 , N为中点,则的长度为.16. 如图1所示,一个三角形纸片的尺寸为: , 将其放置于图2所示的矩形纸板上,首先移动到的位置,接着又移动到的位置,其中点A,B, , 均位于矩形纸板的边上.若在两次移动过程中,恰有 , 则线段的长度等于.
三、解答题
-
17. 计算:(1)、;(2)、.18. 如图,在平行四边形ABCD中, , 垂足分别为M,N.求证:四边形BNDM是矩形.
 19. 如图,在四边形中, , 求四边形的面积.
19. 如图,在四边形中, , 求四边形的面积.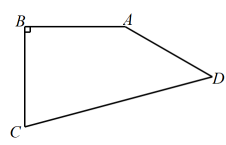 20. 已知.(1)、直接写出 , ;(2)、试求的值;(3)、试求的值.21. 如图所示,由正方形组成的的网格中,每个小正方形的顶点称为格点.等腰直角三角形的顶点均为格点,点M在线段上.请你仅用无刻度直尺按要求完成作图,作图痕迹用虚线表示.
20. 已知.(1)、直接写出 , ;(2)、试求的值;(3)、试求的值.21. 如图所示,由正方形组成的的网格中,每个小正方形的顶点称为格点.等腰直角三角形的顶点均为格点,点M在线段上.请你仅用无刻度直尺按要求完成作图,作图痕迹用虚线表示. (1)、作正方形;(2)、作线段的中点O;(3)、作线段 , 且 , 点E在线段上;(4)、在上作点N,使得.22. 如图所示,在平面直角坐标系中,点 , 轴于点M,点C在x轴的正半轴上,且 , 连接 , .
(1)、作正方形;(2)、作线段的中点O;(3)、作线段 , 且 , 点E在线段上;(4)、在上作点N,使得.22. 如图所示,在平面直角坐标系中,点 , 轴于点M,点C在x轴的正半轴上,且 , 连接 , . (1)、证明:四边形是平行四边形;(2)、当时,求m的值;(3)、当为等腰三角形时,直接写出m的值.
(1)、证明:四边形是平行四边形;(2)、当时,求m的值;(3)、当为等腰三角形时,直接写出m的值.