河南省洛阳市2022-2023学年八年级下学期期中数学试题

试卷更新日期：2023-05-09 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，为估计池塘岸边A，B间的距离，小方在池塘的一侧选取一点O，测得 $O A = 15$ 米， $O B = 10$ 米，A、B间的距离不可能是（）

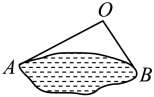A、20米 B、15米 C、10米 D、5米

查看试题解析
2. 如图，若要将一块不能弯曲的正方形（不考虑厚度）搬进室内，需要通过一扇高为2m，宽为1m的门，以下边长的木块中哪块可以通过此门？（）

A、2.8m B、2.5m C、2.2m D、以上答案都不对

查看试题解析
3. 如图，在 $△ A B C$ 中，点A的坐标为 $(0 ， 1)$ ，点C的坐标为 $(4 ， 3)$ ，若图中有一点D使 $△ A B D$ 与 $△ A B C$ 全等，则点D的坐标是（）

A、 $(4 ， - 1)$ B、 $(- 1 ， 3)$ C、 $(- 1 ， - 1)$ D、以上都可以

查看试题解析
4. 小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（）

A、角的内部到角的两边的距离相等的点在角的平分线上 B、角平分线上的点到这个角两边的距离相等 C、三角形三条角平分线的交点到三条边的距离相等 D、以上均不正确

查看试题解析
5. 如图是两个大小不同的量角器.小量角器由于长时间使用，某些刻度已经模糊不清.现将两个量角器的零刻度线放在同一直线上，使 $O_{2}$ 与C重合（如下图）.如果两个半圆的公共点P在大量角器上对应的度数为 $140 °$ ，那么在小量角器上对应的度数为（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $70 °$

查看试题解析
6. 若x为实数，在 $(\sqrt{3} + 1) □ x$ 的“ $□$ ”中添上一种运算符号（在＋，－，×，÷中选择）后，其运算的结果是有理数，则x不可能的是（）

A、 $\sqrt{3} + 1$ B、 $\sqrt{3} - 1$ C、 $2 \sqrt{3}$ D、 $1 - \sqrt{3}$

查看试题解析
7. 有足够多张如图所示的 $A$ 类、 $B$ 类正方形卡片和 $C$ 类长方形卡片，若要拼一个长为 $(3 a + 2 b)$ 、宽为 $(a + b)$ 的大长方形，则需要 $C$ 类卡片的张数为（）

A、3 B、4 C、5 D、6

查看试题解析
8. 我市防汛办为解决台风季排涝问题，准备在一定时间内铺设一条长4000米的排水管道，实际施工时，____.求原计划每天铺设管道多少米？题目中部分条件被墨汁污染，小明查看了参考答案为：“设原计划每天铺设管道x米，则可得方程 $\frac{4000}{x - 10} - \frac{4000}{x} = 20$ ， …”根据答案，题中被墨汁污染条件应补为（）

A、每天比原计划少铺设10米，结果延期20天完成 B、每天比原计划多铺设10米，结果延期20天完成 C、每天比原计划少铺设10米，结果提前20天完成 D、每天比原计划多铺设10米，结果提前20天完成

查看试题解析
9. 如图1是一座立交桥的示意图（道路宽度忽略不计），A为入口，F，G为出口，其中直行道为AB，CG，EF，且AB＝CG＝EF；弯道为以点O为圆心的一段弧，且所对的圆心角均为90°.甲、乙两车由A口同时驶入立交桥，均以8m/s的速度行驶，从不同出口驶出，其间两车到点O的距离y（m）与时间x（s）的对应关系如图2所示，结合题目信息，下列说法错误的是（）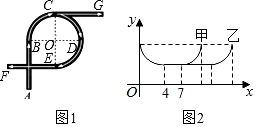

A、立交桥总长为168 m B、从F口出比从G口出多行驶48m C、甲车在立交桥上共行驶11 s D、甲车从F口出，乙车从G口出

查看试题解析
10. 如图，将△ABC沿DE、EF翻折，顶点A，B均落在点O处，且EA与EB重合于线段EO，若∠CDO+∠CFO＝100°，则∠C的度数为（）

A、40° B、41° C、42° D、43°

查看试题解析

二、填空题

11. 如图，在正方形网格中，每个小正方形的边长都是1，有 $A B ， C D ， E F ， G H$ 四条线段，其中能构成直角三角形三边的线段是.

查看试题解析
12. 下图是可调躺椅示意图（数据如图）， $A E$ 与 $B D$ 的交点为 $C$ ，且 $∠ A$ ， $∠ B$ ， $∠ E$ 保持不变．为了舒适，需调整 $∠ D$ 的大小，使 $∠ E F D = 110 °$ ，则图中 $∠ D$ 应（填“增加”或“减少”）度．

查看试题解析
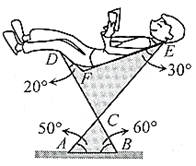13. 有两个正方形A、B，现将B放在A的内部得图甲，将A、B并列放置后构造新的正方形得图乙，若图甲和图乙中阴影部分的面积分别为2和20，则正方形A，B的面积之和为.

查看试题解析
14. 平面直角坐标系中，点 $A (1 ， 3) ， B (- 1 ， - 1) ， C (3 ， a)$ 在同一条直线上，则a的值为.

查看试题解析
15. 甲、乙两人骑自行车从相距s千米的两地同时出发，若同向而行，经过a小时甲追上乙；若相向而行，经过b小时甲、乙相遇.设甲的速度为 $v_{1}$ 千米/小时，乙的速度为 $v_{2}$ 千米/小时，则用字母a，b表示 $\frac{v_{1}}{v_{2}}$ 为.

查看试题解析

三、解答题

16. 先化简，再求值： $(\frac{3}{m + 2} + m - 2) \div \frac{m^{2} - 2 m + 1}{3 m + 6}$ ，其中m= $\sqrt{3}$ +1

查看试题解析
17. 某居民小区有块形状为长方形的绿地 $A B C D$ ，长 $B C$ 为 $\sqrt{128}$ 米，宽 $A B$ 为 $\sqrt{50}$ 米，现在要长方形绿地中修建两个形状大小相同的长方形花坛（即图中阴影部分），每个长方形花坛的长为 $(\sqrt{13} + 1)$ 米，宽为 $(\sqrt{13} - 1)$ 米.

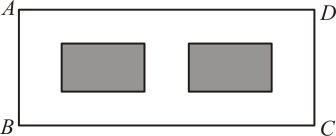(1)、求长方形 $A B C D$ 的周长.（结果化为最简二次根式）

(2)、除去修建花坛的地方，其它地方全修建成通道，通道上要铺上造价为30元/平方米的地砖，要铺完整个通道，则购买地砖需要花费多少元？

查看试题解析
18. 在一条东西走向河的一侧有一村庄C，河边原有两个取水点A，B，其中 $A B = A C$ ，由于种种原因，由C到A的路现在已经不通了，某村为方便村民取水决定在河边新建一个取水点H（A，H，B在一条直线上），并新修一条路 $C H$ ，测得 $C B = 3$ 千米， $C H = 2.4$ 千米， $H B = 1.8$ 千米.

(1)、问 $C H$ 是不是从村庄C到河边的最近路，请通过计算加以说明；

(2)、求原来的路线 $A C$ 的长.

查看试题解析
19. 如图，在平面直角坐标系中，一次函数 $y_{1} = k x + b (k \neq 0)$ 的图像与反比例函数 $y_{2} = \frac{m}{x} (m \neq 0)$ 的图像相交于第一、三象限内的 $A (3 ， 5) ， B (a ， - 3)$ 两点，与x轴交于点C.

(1)、求该反比例函数和一次函数的解析式；

(2)、不等式 $k x + b > \frac{m}{x}$ 的解集是；

(3)、在y轴上找一点P使 $P B - P C$ 最大，求 $P B - P C$ 的最大值及点P的坐标.

查看试题解析
20. 综合与实践
数学活动课上，老师让同学们以“过等腰三角形顶点的直线”为主题开展数学探究.

(1)、操作发现：如图甲，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ，且 $A B = A C$ ，直线l经过点A.小华分别过B、C两点作直线l的垂线，垂足分别为点D、E.易证 $△ A B D ≌ △ C A E$ ，此时，线段 $D E$ 、 $B D$ 、 $C E$ 的数量关系为：；

(2)、拓展应用：
如图乙， $△ A B C$ 为等腰直角三角形， $∠ A C B = 90 °$ ，已知点C的坐标为 $(- 2 ， 0)$ ，点B的坐标为 $(1 ， 2)$ .请利用小华的发现直接写出点A的坐标：；

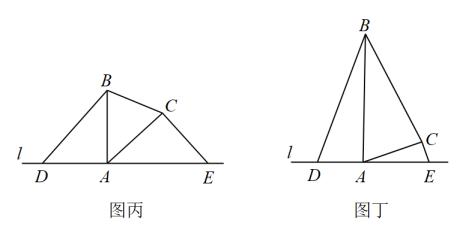
(3)、迁移探究：
①如图丙，小华又作了一个等腰 $△ A B C$ ， $A B = A C$ ，且 $∠ B A C \neq 90 °$ ，她在直线l上取两点D、E，使得 $∠ B A C = ∠ B D A = ∠ A E C$ ，请你帮助小华判断（1）中线段 $D E$ 、 $B D$ 、 $C E$ 的数量关系是否变化，若不变，请证明；若变化，写出它们的关系式并说明理由；
②如图丁， $△ A B C$ 中， $A B = 2 A C$ ， $∠ B A C \neq 90 °$ ，点D、E在直线 $l$ 上，且 $∠ B A C = ∠ B D A = ∠ A E C$ ，请直接写出线段 $D E$ 、 $B D$ 、 $C E$ 的数量关系.

查看试题解析