福建省泉州市泉港区2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-05-09 类型:期中考试
一、单选题
-
1. 若点在第二象限,且到轴的距离是3,到轴的距离是1,则点的坐标是( )A、 B、 C、 D、2. 下列图象中,表示y是x的函数的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在中对角线和交于O,若 , 则边长的取值范围是( )A、 B、 C、 D、4. 如下图,同一坐标系中,直线l1: y=2x-3和l2: y=-3x+2的图象大致是( )A、
3. 在中对角线和交于O,若 , 则边长的取值范围是( )A、 B、 C、 D、4. 如下图,同一坐标系中,直线l1: y=2x-3和l2: y=-3x+2的图象大致是( )A、 B、
B、 C、
C、 D、
D、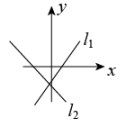 5. 下列四个选项中,不符合直线的性质特征的选项是( )A、经过第二、三、四象限 B、y随x的增大而减小 C、与x轴交于 D、与y轴交于6. 如图,在3×3的正方形网格中,以线段AB为对角线作平行四边形,使另两个顶点也在格点上,则这样的平行四边形最多可以画( )
5. 下列四个选项中,不符合直线的性质特征的选项是( )A、经过第二、三、四象限 B、y随x的增大而减小 C、与x轴交于 D、与y轴交于6. 如图,在3×3的正方形网格中,以线段AB为对角线作平行四边形,使另两个顶点也在格点上,则这样的平行四边形最多可以画( ) A、2个 B、3个 C、4个 D、5个7. 如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为
A、2个 B、3个 C、4个 D、5个7. 如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为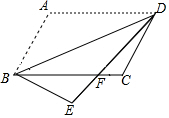 A、 B、 C、 D、8. 在平行四边形ABCD中,于点E,于点F,若 , , 平行四边形的ABCD周长为40,则( )
A、 B、 C、 D、8. 在平行四边形ABCD中,于点E,于点F,若 , , 平行四边形的ABCD周长为40,则( )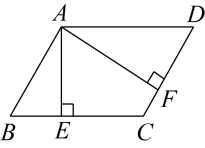 A、24 B、36 C、40 D、489. 若点 , , 在反比例函数图象上,则下列结论正确的是( )A、 B、 C、 D、10. 如图,线段 , 是线段上方的一点, , 在的同制作等边、等边和等边 , 则下列结论:
A、24 B、36 C、40 D、489. 若点 , , 在反比例函数图象上,则下列结论正确的是( )A、 B、 C、 D、10. 如图,线段 , 是线段上方的一点, , 在的同制作等边、等边和等边 , 则下列结论:
①;②;③四边形是平行四边形;④四边形面积的最大值是.其中正确的是( )
A、①③ B、①②③ C、①③④ D、②③④二、填空题
-
11. 点关于轴的对称点的坐标为.12. 函数:y=中,自变量x的取值范围是13. 如图,平行四边形ABCD的周长是12cm,对角线AC,BD相交于点O,OE⊥BD交AD于点E;则△ABE的周长为cm.
 14. 如图,直线和相交于点 , 则不等式的解集为.
14. 如图,直线和相交于点 , 则不等式的解集为. 15. 如图,中, , 则的长为.
15. 如图,中, , 则的长为. 16. 如图,平行四边形的顶点在轴的正半轴上,点在对角线上,反比例函数的图像经过两点,已知平行四边形的面积是 , 则点的坐标为.
16. 如图,平行四边形的顶点在轴的正半轴上,点在对角线上,反比例函数的图像经过两点,已知平行四边形的面积是 , 则点的坐标为.
三、解答题
-
17. 已知一次函数 的图象经过点 和点 ,求当 时,函数y的值.18. 如图,在中,过对角线的交点 , 且与边分别相交于点 , , 求四边形的周长.
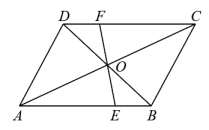 19. 已知:如图,在中,于点.
19. 已知:如图,在中,于点.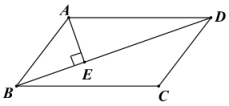 (1)、求作:线段 , 使得于点(请用无刻度的直尺与圆规作图,不写作法和证明,但要保留作图痕迹)(2)、在(1)的条件下,求证:.20. 如图,正比例函数y=kx与反比例函数 (x>0)的图象相交于点A(2,2),将直线y=kx向下平移,得到直线l.若直线l与该反比例函数的图象相交于点B(3,n).
(1)、求作:线段 , 使得于点(请用无刻度的直尺与圆规作图,不写作法和证明,但要保留作图痕迹)(2)、在(1)的条件下,求证:.20. 如图,正比例函数y=kx与反比例函数 (x>0)的图象相交于点A(2,2),将直线y=kx向下平移,得到直线l.若直线l与该反比例函数的图象相交于点B(3,n). (1)、求m,n的值;(2)、连结AB,OB,求△AOB的面积.21. 如图①,某乘客乘高速列车从甲地经过乙地到丙地,列车匀速行驶,图②为列车离乙地路程y(千米)与行驶时间x(小时)的函数关系图象.
(1)、求m,n的值;(2)、连结AB,OB,求△AOB的面积.21. 如图①,某乘客乘高速列车从甲地经过乙地到丙地,列车匀速行驶,图②为列车离乙地路程y(千米)与行驶时间x(小时)的函数关系图象. (1)、填空:甲、丙两地距离千米;(2)、求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围.22. 在中, , D是斜边上的一点,作 , 垂足为E,延长到F,连结 , 使.
(1)、填空:甲、丙两地距离千米;(2)、求高速列车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围.22. 在中, , D是斜边上的一点,作 , 垂足为E,延长到F,连结 , 使. (1)、求证:四边形是平行四边形;(2)、连接 , 若平分 , , 求四边形的面积.23. 为了迎接五一黄金周的购物高峰,某品牌专卖店准备购进甲、乙两种运动鞋,其中甲、乙两种运动鞋的进价和售价如下表:
(1)、求证:四边形是平行四边形;(2)、连接 , 若平分 , , 求四边形的面积.23. 为了迎接五一黄金周的购物高峰,某品牌专卖店准备购进甲、乙两种运动鞋,其中甲、乙两种运动鞋的进价和售价如下表:运动鞋价格
甲
乙
进价(元/双)
售价(元/双)
240
160
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)、求的值.(2)、若购进乙种运动鞋(双),要使购进的甲、乙两种运动鞋共200双的总利润(元)(利润=售价-进价)不少于13000元且不超过13500元,问:购进甲种运动鞋多少双时总利润最大,最大利润是多少?24. 在平行四边形ABCD中,点O是对角线BD中点,点E在边BC上,EO的延长线与边AD交于点F,连接BF、DE,如图1. (1)、求证:四边形BEDF是平行四边形;(2)、在(1)中,若DE=DC,∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、R,如图2.
(1)、求证:四边形BEDF是平行四边形;(2)、在(1)中,若DE=DC,∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、R,如图2.①当CD=6,CE=4时,求BE的长.
②探究BH与AF的数量关系,并给予证明.
25. 如图1,在平面直角坐标系xOy中,点O是坐标原点,直线: 与直线:交于点A,两直线与x轴分别交于点和. (1)、求直线和的表达式.(2)、点P是y轴上一点,当最小时,求点P的坐标.(3)、如图2,点D为线段上一动点,将沿直线翻折得到 , 线段交x轴于点F,若为直角三角形,求点D坐标.
(1)、求直线和的表达式.(2)、点P是y轴上一点,当最小时,求点P的坐标.(3)、如图2,点D为线段上一动点,将沿直线翻折得到 , 线段交x轴于点F,若为直角三角形,求点D坐标.