湖北省孝感市云梦县2023年中考数学模拟试卷

试卷更新日期：2023-05-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 给出下列结论： $①$ 一个有理数的 $3$ 倍大于这个有理数； $②$ 绝对值最小的整数是 $0$ ； $③$ 规定了原点和单位长度的直线叫数轴； $④$ 如果 $| a | = a$ ，那么 $a > 0$ ； $⑤$ 不是正数的数一定是负数.其中正确结论的个数为（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
2. 截至北京时间5月14日6时30分，全球累计确诊新冠肺炎病例超过435万例.用科学记数法表示435万是（）.

A、 $4.35 \times 10^{5}$ B、 $43.5 \times 10^{5}$ C、 $0.435 \times 10^{7}$ D、 $4.35 \times 10^{6}$

查看试题解析
3. 下列几何体中，主视图是圆的是（）

A、球 B、正方体 C、三棱锥 D、圆柱

查看试题解析
4. 下列运算正确的是（）

A、 $a^{3} \cdot a^{2} = a^{6}$ B、 $a^{5} + a^{5} = a^{10}$ C、 ${(a + b)}^{2} = a^{2} + b^{2}$ D、 ${(a^{2})}^{3} = a^{6}$

查看试题解析
5. 在物理实验课上，小明用弹簧称将铁块A悬于盛有水的水槽中，然后匀速向上提起，直至铁块完全露出水面一定高度，则下图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析
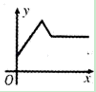6. 下列调查中，适宜采用抽样调查的是（）

A、对飞机零部件质量的调查 B、对全班45位同学身高的调查 C、对动车站客流量的调查 D、对全运会运动员使用兴奋剂的调查

查看试题解析
7. 如图，BD是△ABC的角平分线，DE是BC的垂直平分线，∠A=90°，AD=2，则CD的长为（）

A、3 $\sqrt{3}$ B、6 C、5 D、4

查看试题解析
8. 以下列各组数据为边长，可以构成等腰三角形的是（）

A、1，1，2 B、1，1，3 C、2，2，1 D、2，2，5

查看试题解析

二、填空题

9.
观光塔是潍坊市区的标志性建筑，为测量其高度，如图，一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°，然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°．已知楼房高AB约是45m，根据以上观测数据可求观光塔的高CD是 m．

查看试题解析
10. 在函数 $y = \frac{x}{1 + 2 x}$ 中，自变量x的取值范围是.

查看试题解析
11. 已知，正多边形的每个内角为150°，则这个多边形的对角线共有条.

查看试题解析
12. 对于实数a，b，定义运算“*”：a*b= ${\begin{array}{l} a^{2} - a b (a \geq b) \\ \frac{b - a}{a} (a < b) \end{array}$ 例如3*1，因为3＞1，所以3*1=3²-3×1=6.若x₁ ， x₂是一元二次方程x²-4=0的两个根，则x₁*x₂=.

查看试题解析
13. 如图，有四张扑克牌，分别是红桃 $4$ ，黑桃 $2$ ，方块 $8$ ，梅花 $6$ ，它们的背面都相同，现将它们背面朝上洗匀后，从中任意摸出一张，记下牌面数字后放回，再将它们背面朝上洗匀，从中再任意摸出一张，记下牌面数字，则两次牌面数字都是 $4$ 的倍数的概率是 .

查看试题解析
14. 如图，在扇形CBA中，∠ACB＝90°，连接AB，以BC为直径作半圆，交AB于点D.若阴影部分的面积为（π-1），则阴影部分的周长为.

查看试题解析
15. 如图，在平面直角坐标系中，一颗棋子从点P处开始跳动，第一次跳到点P关于x轴的对称点 $P_{1}$ 处，接着跳到点 $P_{1}$ 关于 $y$ 轴的对称点 $P_{2}$ 处，第三次再跳到点 $P_{2}$ 关于原点的对称点处， $\dots$ ，如此循环下去.当跳动第 $2009$ 次时，棋子落点处的坐标是.

查看试题解析
16. 如图， $△ A B C$ 中， $∠ A B C = 60 ° (A B < A C)$ ， D为边 $A C$ 上的点， $∠ A D B = 45 °$ ， $A C = \frac{7 \sqrt{3}}{3}$ ， $B D = 3 \sqrt{2}$ ，则 $A B$ 长是 .

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{9} - {(- 2)}^{2} + {(- 0.25)}^{0}$ ；

(2)、 ${(x - 2)}^{2} - (x - 3) (x - 1)$ .

查看试题解析
18. 为拓展学生视野，促进书本知识与生活实践的深度融合，某中学组织八年级全体学生开展研学活动.在此次活动中，若每名老师带队14名学生，则还剩10名学生没老师带；若每名老师带队15名学生，就有1名老师少带6名学生，现有甲、乙两种大型客车，它们的载客量和租金如表所示：
客车类型
甲型客车
乙型客车
载客量/（人/辆）
35
30
租金/（元/辆）
400
320
学校计划此次研学活动的租金总费用不超过3000元，且保证所有师生都有车坐，

(1)、参加此次研学活动的老师和学生各有多少人？

(2)、学校打算租甲型客车和乙型客车两种客车总共8辆车，学校共有几种租车方案？最少租车费用是多少？

查看试题解析
19. 2022年5月，某市准备面向全市中学生举办“建设绿色生态家园”主题知识竞赛.为此，某校为筛选参赛选手，举办了“建设绿色生态家园”主题知识答题活动，并将随机抽取的部分学生的成绩划分为A，B，C，D四个等级，绘制了不完整的两种统计图：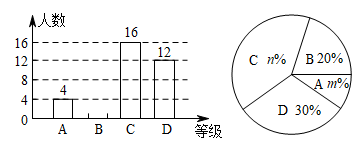
根据以上信息，回答下列问题：

(1)、计算成绩为B等级的学生数，并把条形图补充完整；

(2)、求扇形统计图中m的值；

(3)、求出扇形统计图中C部分的圆心角的度数.

查看试题解析
20. 如图，在锐角 $△ A B C$ 中， $A C$ 是最短边；以 $A C$ 中点O为圆心， $\frac{1}{2} A C$ 长为半径作 $⊙ O$ ，交 $B C$ 于E，过O作 $O D ∥ B C$ 交 $⊙ O$ 于D，连接 $A E$ 、 $A D$ 、 $D C$ .

(1)、求证：D是 $\overset{⌢}{A E}$ 的中点；

(2)、求证： $∠ D A O = ∠ B + ∠ B A D$ .

查看试题解析
21. 某衬衣店将进价为30元的一种衬衣以40元售出，平均每月能售出600件，调查表明：这种衬衣售价每上涨1元，其销售量将减少10件．

(1)、写出月销售利润y（单位：元）与售价x（单位：元/件）之间的函数解析式．

(2)、当销售价定为45元时，计算月销售量和销售利润．

(3)、当销售价定为多少元时会获得最大利润？求出最大利润．

查看试题解析
22. 如图在平面直角坐标系中，已知 $A (a ， 0)$ ， $B (b ， 0)$ ， $M (- 1.5 ， - 2)$ ，其中 $a$ 、 $b$ 满足 $| a + 1 | + {(b - 3)}^{2} = 0$ .

(1)、求 $△ A B M$ 的面积；

(2)、在x轴上求一点P，使得 $△ A M P$ 的面积与 $△ A B M$ 的面积相等；

(3)、在y轴上存在使 $△ B M P$ 的面积与 $△ A B M$ 的面积相等的P点，请直接写出点P的坐标.

查看试题解析
23. 如图，抛物线 $y = a x^{2} + b x + 2$ 经过点 $A (- 1 ， 0) ， B (4 ， 0)$ ，与y轴交于点C.

(1)、求抛物线的解析式；

(2)、点D为y轴右侧抛物线上一点，是否存在点D，使 $S_{△ A B C} = \frac{2}{3} S_{△ A B D}$ ？若存在，求出点D的坐标；若不存在，请说明理由；

(3)、将直线BC绕点B顺时针旋转45°，与直线AC交于点F，直接写出BF的长.

查看试题解析

客车类型	甲型客车	乙型客车
载客量/（人/辆）	35	30
租金/（元/辆）	400	320