湖北省咸宁市五校联考2023年九年级下学期3月质量检测数学试题
试卷更新日期:2023-05-09 类型:月考试卷
一、单选题
-
1. 的绝对值是( )A、 B、 C、7 D、-72. 春季天气多变,易滋生细菌,是流感、诺如病毒等传染病的高发期.各校积极开展“多病同防”的系列教育活动.某市卫生部门统计,截止3月15日,全市有万人感染了春季流行病,用科学记数法表示万,正确的是( )A、 B、 C、 D、3. 如图,在△ABC中,点D、E分别是AB、AC的中点,若∠B=40°,则∠BDE的度数为( )
 A、40° B、50° C、140° D、150°4. 下列运算正确的是( )A、 B、 C、 D、5. 如图所示的几何体的俯视图是( )
A、40° B、50° C、140° D、150°4. 下列运算正确的是( )A、 B、 C、 D、5. 如图所示的几何体的俯视图是( ) A、
A、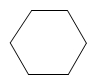 B、
B、 C、
C、 D、
D、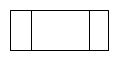 6. 下列说法正确的是( )A、打开电视机,它正在播广告是必然事件 B、掷一枚质地均匀的硬币,正面朝上的概率可能为0 C、一组数据“5,4,6,2,7,4,3”的众数是4,中位数是2 D、从全校1500名学生中抽取100名调查了解寒假阅读情况,抽取的样本容量为1007. 如图,正五边形内接于 , 其半径为1,作交于点F,则的长为( )
6. 下列说法正确的是( )A、打开电视机,它正在播广告是必然事件 B、掷一枚质地均匀的硬币,正面朝上的概率可能为0 C、一组数据“5,4,6,2,7,4,3”的众数是4,中位数是2 D、从全校1500名学生中抽取100名调查了解寒假阅读情况,抽取的样本容量为1007. 如图,正五边形内接于 , 其半径为1,作交于点F,则的长为( ) A、 B、 C、 D、8. 如图①,在矩形中,动点E从点A出发,沿的路线运动,当点E到达点C时停止运动.若 , 交于点F,设点E运动的路程为x, , 已知y关于x的函数图象如图②所示,当时,y的值为( )
A、 B、 C、 D、8. 如图①,在矩形中,动点E从点A出发,沿的路线运动,当点E到达点C时停止运动.若 , 交于点F,设点E运动的路程为x, , 已知y关于x的函数图象如图②所示,当时,y的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
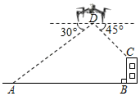
9. 二次根式在实数范围内有意义,则x的取值范围是 .10. 关于x的方程x2﹣x﹣1=0的两根分别为x1、x2则x1+x2﹣x1•x2的值为 .11. 以原点为中心,把抛物线的顶点顺时针旋转 , 得到的点的坐标为 .12. 《孙子算经》是我国传统数学的重要著作之一,其中记载的“荡杯问题”很有趣.其内容为:2人同吃一碗饭,3人同吃一碗羹,4人同吃一碗肉,共用65个碗,问有客人.13. 如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面米的处,无人机测得操控者的俯角为30°,测得点处的俯角为45°.又经过人工测量操控者和教学楼之间的水平距离为80米,教学楼的高度米.(注:点、、、都在同一平面上,参考数据: , 结果保留整数).
 14. 如图, 中, , ,请依据尺规作图的作图痕迹,计算 .
14. 如图, 中, , ,请依据尺规作图的作图痕迹,计算 .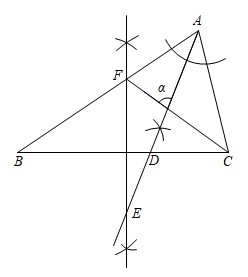 15. 我国古代数学家杨辉发现了如图所示的三角形,后人称它为“杨辉三角”,它具有一定的规律性,从图中取一斜列数:1,3,6,10,15,我们把第一个数记为 , 第二个数记为 , 第三个数记为 , …第n个数记为 , 则 .
15. 我国古代数学家杨辉发现了如图所示的三角形,后人称它为“杨辉三角”,它具有一定的规律性,从图中取一斜列数:1,3,6,10,15,我们把第一个数记为 , 第二个数记为 , 第三个数记为 , …第n个数记为 , 则 . 16. 如图,四边形为正方形,的平分线交于点E,将绕点B顺时针旋转90°得到 , 延长交于点G,连接 , , 与相交于点H.有下列结论:①;②G为的外心;③;④ . 其中正确结论的序号是 .
16. 如图,四边形为正方形,的平分线交于点E,将绕点B顺时针旋转90°得到 , 延长交于点G,连接 , , 与相交于点H.有下列结论:①;②G为的外心;③;④ . 其中正确结论的序号是 .
三、解答题
-
17. 计算:(π﹣1)0+| ﹣2|﹣( )﹣1+tan60°.18. 京东快递仓库使用机器人分拣货物,已知一台机器人的工作效率相当于一名分拣工人工作效率的20倍,若用一台机器人分栋8000件货物,比原先16名工人分拣这些货物要少小时.求一台机器人一小时可分拣多少件货物?19. 今年九年级体育中考选考项目是从篮球(用A表示)、排球(用B表示)和足球(用C表示)中选一项.
 (1)、如图是某校九年级同学选考项目的扇形统计图,则选考足球所对应的扇形圆心角为 .(2)、用画树状图或列表法求李强、王丽两位同学选择同一选考项目的概率.20. 如图,一次函数的图象与反比例函数的图象交于点A,B,与x轴交于点F,与y轴交于点C.点A的坐标为 , 点B的坐标为 .
(1)、如图是某校九年级同学选考项目的扇形统计图,则选考足球所对应的扇形圆心角为 .(2)、用画树状图或列表法求李强、王丽两位同学选择同一选考项目的概率.20. 如图,一次函数的图象与反比例函数的图象交于点A,B,与x轴交于点F,与y轴交于点C.点A的坐标为 , 点B的坐标为 . (1)、求一次函数和反比例函数的关系式;(2)、若点E是点C关于x轴的对称点,求的面积;(3)、将直线向上平移5个单位得到直线 , 当函数值时,直接写出x的取值范围.21. 如图,是的直径,点C,D在上, , 与相交于点E,点F在的延长线上,且 .
(1)、求一次函数和反比例函数的关系式;(2)、若点E是点C关于x轴的对称点,求的面积;(3)、将直线向上平移5个单位得到直线 , 当函数值时,直接写出x的取值范围.21. 如图,是的直径,点C,D在上, , 与相交于点E,点F在的延长线上,且 . (1)、求证:是的切线;(2)、若 , , 求的半径.22. 李丽大学毕业后回家乡创业,开了一家服装专卖店代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),每天付员工的工资每人82元,每天应支付其他费用106元.
(1)、求证:是的切线;(2)、若 , , 求的半径.22. 李丽大学毕业后回家乡创业,开了一家服装专卖店代理品牌服装的销售.已知该品牌服装进价每件40元,日销售y(件)与销售价x(元/件)之间的关系如图所示(实线),每天付员工的工资每人82元,每天应支付其他费用106元. (1)、直接写出日销售y(件)与销售价x(元/件)之间的函数关系式;(2)、当某天的销售价为48元/件时,收支恰好平衡(收入=支出),求该店员工人数;(3)、若该店只有2名员工,则每天能获得的最大利润是多少元?此时,每件服装的价格应定为多少元?23. 等边中,是中线,一个以点D为顶点的30°角绕点D旋转,使角的两边分别与 , 的延长线相交于点E,F.交于点M,交于点N.
(1)、直接写出日销售y(件)与销售价x(元/件)之间的函数关系式;(2)、当某天的销售价为48元/件时,收支恰好平衡(收入=支出),求该店员工人数;(3)、若该店只有2名员工,则每天能获得的最大利润是多少元?此时,每件服装的价格应定为多少元?23. 等边中,是中线,一个以点D为顶点的30°角绕点D旋转,使角的两边分别与 , 的延长线相交于点E,F.交于点M,交于点N.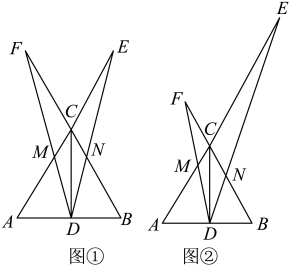 (1)、如图①,若 , 求证: .(2)、如图②,在绕点D旋转的过程中:
(1)、如图①,若 , 求证: .(2)、如图②,在绕点D旋转的过程中:①探究三条线段 , , 之间的数量关系,并说明理由;
②若 , , 求的长.
24. 如图,抛物线与x轴交于点A,点B,与y轴交于点C,其对称轴为 . 过点A的直线与抛物线交于另一点E.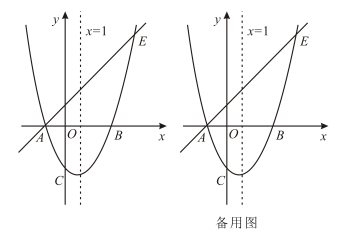 (1)、该抛物线的解析式为;(2)、点Q是轴上的一动点,当为等腰三角形时,直接写出Q点的坐标;(3)、点P是第四象限内抛物线上的一个点,过点P作于H.若取得最大值时,求这个最大值:(4)、M是抛物线对称轴上一点,过M点作轴于点N.当最短时,求点M的坐标.
(1)、该抛物线的解析式为;(2)、点Q是轴上的一动点,当为等腰三角形时,直接写出Q点的坐标;(3)、点P是第四象限内抛物线上的一个点,过点P作于H.若取得最大值时,求这个最大值:(4)、M是抛物线对称轴上一点,过M点作轴于点N.当最短时,求点M的坐标.