湖北省仙桃市2023年中考数学模拟训练卷
试卷更新日期:2023-05-09 类型:中考模拟
一、单选题
-
1. 在下列各数中是无理数的有( )
-0.333…, , , -π,2.0101001…(相邻两个1之间增加1个0)
A、3个 B、4个 C、5个 D、2个2. 如图所示几何体是由一个球体和一个圆柱组成的,它的俯视图是( )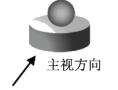 A、
A、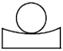 B、
B、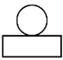 C、
C、 D、
D、 3. “中国疫苗,助力全球战疫”据法国《费加罗报》网站10月15日报道,预计到今年年底,全球新冠疫苗产量将超过120亿剂,其中一半将来自中国制造商,这是欧盟计划在2021年生产的30亿剂新冠疫苗数量的两倍中国已经向全球100多个国家提供了疫苗数据120亿剂用科学记数法表示为( )A、0.12×1011剂 B、1.2×1010剂 C、12×109剂 D、120×108剂4. 如图,直线 ,直线 ,若 ,则 ( )
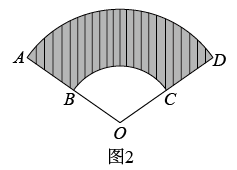
3. “中国疫苗,助力全球战疫”据法国《费加罗报》网站10月15日报道,预计到今年年底,全球新冠疫苗产量将超过120亿剂,其中一半将来自中国制造商,这是欧盟计划在2021年生产的30亿剂新冠疫苗数量的两倍中国已经向全球100多个国家提供了疫苗数据120亿剂用科学记数法表示为( )A、0.12×1011剂 B、1.2×1010剂 C、12×109剂 D、120×108剂4. 如图,直线 ,直线 ,若 ,则 ( )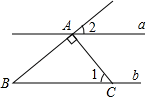 A、 B、 C、 D、5. 下列说法正确的是( )A、了解我市市民知晓“礼让行人”交通新规的情况,适合全面调查 B、甲、乙两人跳远成绩的方差分别为S甲2=3,S乙2=4,说明乙的跳远成绩比甲稳定 C、一组数据2,2,3,4的众数是2,中位数是2.5 D、可能性是1%的事件在一次试验中一定不会发生6. 下列计算正确的是( )A、 B、 C、 D、7. 反比例函数 ,下列说法不正确的是( )A、图象经过点(1,-3) B、图象位于第二、四象限 C、图象关于直线y=x对称 D、y随x的增大而增大8. 已知 , 是方程的两个实数根,则代数式的值是( )A、4045 B、4044 C、2022 D、19. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角 形成的扇面,若 , ,则阴影部分的面积为( )
A、 B、 C、 D、5. 下列说法正确的是( )A、了解我市市民知晓“礼让行人”交通新规的情况,适合全面调查 B、甲、乙两人跳远成绩的方差分别为S甲2=3,S乙2=4,说明乙的跳远成绩比甲稳定 C、一组数据2,2,3,4的众数是2,中位数是2.5 D、可能性是1%的事件在一次试验中一定不会发生6. 下列计算正确的是( )A、 B、 C、 D、7. 反比例函数 ,下列说法不正确的是( )A、图象经过点(1,-3) B、图象位于第二、四象限 C、图象关于直线y=x对称 D、y随x的增大而增大8. 已知 , 是方程的两个实数根,则代数式的值是( )A、4045 B、4044 C、2022 D、19. 如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角 形成的扇面,若 , ,则阴影部分的面积为( )
 A、 B、 C、 D、10. 如图,菱形中,.动点P从点B出发,以每秒1个单位长度的速度沿折线运动到点C,同时动点Q从点A出发,以相同速度沿折线运动到点D,当一个点停止运动时,另一点也随之停止.设的面积为y,运动时间为x秒.则下列图象能大致反映y与x之间函数关系的是( )
A、 B、 C、 D、10. 如图,菱形中,.动点P从点B出发,以每秒1个单位长度的速度沿折线运动到点C,同时动点Q从点A出发,以相同速度沿折线运动到点D,当一个点停止运动时,另一点也随之停止.设的面积为y,运动时间为x秒.则下列图象能大致反映y与x之间函数关系的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
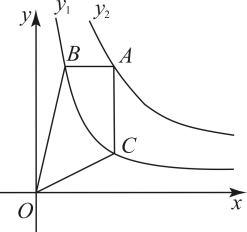
11. 分解因式:.12. 解诗谜:悟空顺风探妖踪,千里只用四分钟;归时四分行六百,试问风速是多少?题目的意思是:孙悟空追寻妖精的行踪,去时顺风,1000里只用了4分钟;回来时逆风,4分钟只走了600里,试求风的速度为.13. 一个不透明的口袋中有四个完全相同的小球,其上分别标有数字1,2,4,8.随机摸取一个小球后不放回,再随机摸取一个小球,则两次取出的小球上数字之积等于8的概率是 .14. 如图,点A是反比例函数的图象上的一动点,过点A分别作x轴、y轴的平行线,与反比例函数( , )的图象交于点B、点C,连接 , . 若四边形的面积为5,则 .
 15. 如图AB为⊙O的直径,点P为AB延长线上的点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是(写所有正确论的号)
15. 如图AB为⊙O的直径,点P为AB延长线上的点,过点P作⊙O的切线PE,切点为M,过A、B两点分别作PE垂线AC、BD,垂足分别为C、D,连接AM,则下列结论正确的是(写所有正确论的号)①AM平分∠CAB;② ;③若AB=4,∠APE=30°,则 的长为 ;④若AC=3BD,则有tan∠MAP= .

三、解答题
-
16.(1)、计算: .(2)、先化简,再求值 ,其中 为方程 的根.17. 请用无刻度直尺按要求画图,不写画法,保留画图痕迹(用虚线表示画图过程,实线表示画图结果).
 (1)、如图1, 、 、 是边长为1的正方形网格的格点,作 的高 和 ;(2)、如图2,点 是半 内一点,过点 作直线 直径 于点 .18. 为调查某市市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“ :自行车, :家庭汽车, :公交车, :电动车, :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
(1)、如图1, 、 、 是边长为1的正方形网格的格点,作 的高 和 ;(2)、如图2,点 是半 内一点,过点 作直线 直径 于点 .18. 为调查某市市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“ :自行车, :家庭汽车, :公交车, :电动车, :其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
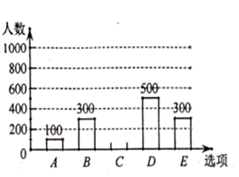 (1)、本次调查中,一共调查了名市民;扇形统计图中, 项对应的扇形圆心角是 .(2)、补全条形统计图.(3)、若甲上班时从A、B、C三种交通工具中随机选择一种, 乙上班时从B、C、D三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选 种交通工具上班的概率.19. 已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.
(1)、本次调查中,一共调查了名市民;扇形统计图中, 项对应的扇形圆心角是 .(2)、补全条形统计图.(3)、若甲上班时从A、B、C三种交通工具中随机选择一种, 乙上班时从B、C、D三种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人都不选 种交通工具上班的概率.19. 已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.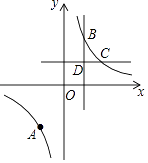 (1)、当y1﹣y2=4时,求m的值;
(1)、当y1﹣y2=4时,求m的值;
(2)、如图,过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x轴上,若三角形PBD的面积是8,请写出点P坐标(不需要写解答过程).
20. 如图,小树在路灯O的照射下形成投影.若树高 , 树影 , 树与路灯的水平距离 , 求路灯的高度. 21. 如图,△ABC内接于⊙O,AC是⊙O的直径,过OA上的点P作PD⊥AC,交CB的延长线于点D,交AB于点E,点F为DE的中点,连接BF.
21. 如图,△ABC内接于⊙O,AC是⊙O的直径,过OA上的点P作PD⊥AC,交CB的延长线于点D,交AB于点E,点F为DE的中点,连接BF. (1)、求证:BF与⊙O相切;(2)、若AP=OP,cosA= , AP=4,求BF的长.22. 为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据场调查,在草莓上市销售的30天中,其销售价格 (元/公斤)与第 天之间满足 ( 为正整数),销售量 (公斤)与第 天之间的函数关系如图所示:
(1)、求证:BF与⊙O相切;(2)、若AP=OP,cosA= , AP=4,求BF的长.22. 为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据场调查,在草莓上市销售的30天中,其销售价格 (元/公斤)与第 天之间满足 ( 为正整数),销售量 (公斤)与第 天之间的函数关系如图所示:如果李大爷的草莓在上市销售期间每天的维护费用为80元.
 (1)、求销售量 与第 天之间的函数关系式;(2)、求在草莓上市销售的30天中,每天的销售利润 与第 天之间的函数关系式;(日销售利润=日销售额﹣日维护费)(3)、求日销售利润 的最大值及相应的 .23. 已知:点C,D均在直线l的上方,与都是直线l的垂线段,且在的右侧, , 与相交于点O.
(1)、求销售量 与第 天之间的函数关系式;(2)、求在草莓上市销售的30天中,每天的销售利润 与第 天之间的函数关系式;(日销售利润=日销售额﹣日维护费)(3)、求日销售利润 的最大值及相应的 .23. 已知:点C,D均在直线l的上方,与都是直线l的垂线段,且在的右侧, , 与相交于点O.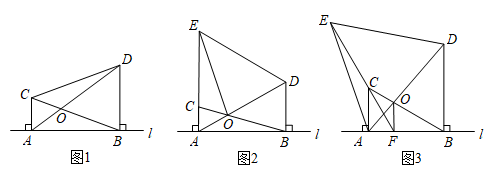 (1)、如图1,若连接 , 则的形状为 , 的值为;(2)、若将沿直线l平移,并以为一边在直线l的上方作等边.
(1)、如图1,若连接 , 则的形状为 , 的值为;(2)、若将沿直线l平移,并以为一边在直线l的上方作等边.①如图2,当与重合时,连接 , 若 , 求的长;
②如图3,当时,连接并延长交直线l于点F,连接.求证:.
24. 如图,已知二次函数y=﹣x2+bx+c(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.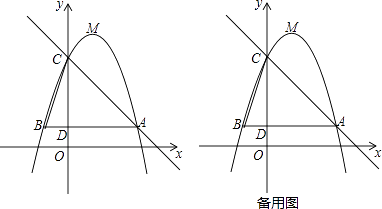 (1)、求该二次函数的解析式及点M的坐标;(2)、若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)、点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
(1)、求该二次函数的解析式及点M的坐标;(2)、若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;(3)、点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).