湖北省武汉市江夏区2023年九年级下学期3月月考数学试卷
试卷更新日期:2023-05-09 类型:月考试卷
一、单选题
-
1. 2023的相反数是( )A、 B、 C、 D、20232. 在“石头、剪刀、布”游戏中,对方出“剪刀”.这个事件是( )A、必然事件 B、随机事件 C、不可能事件 D、确定性事件3. 下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( )A、 B、 C、 D、5. 如图所示的几何体的俯视图是( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 如图所示的几何体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、7. 如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形的面积为 , 小正方形与大正方形重叠部分的面积为 , 若 , 则S随t变化的函数图象大致为( )
6. 若点 , , 都在反比例函数的图象上,则 , , 的大小关系是( )A、 B、 C、 D、7. 如图,边长分别为1和2的两个正方形,其中有一条边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为t,大正方形的面积为 , 小正方形与大正方形重叠部分的面积为 , 若 , 则S随t变化的函数图象大致为( )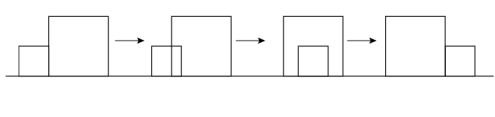 A、
A、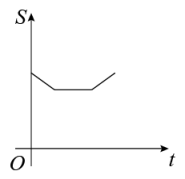 B、
B、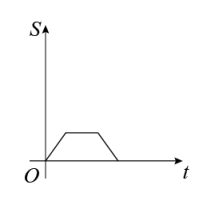 C、
C、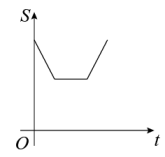 D、
D、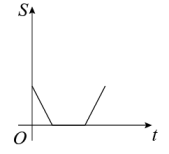 8. 某校团支部组织部分共青团员开展学雷锋志愿者服务活动,每个志愿者都可以从以下三个项目中任选一项参加:①敬老院做义工;②文化广场地面保洁;③路口文明岗值勤.则小明和小慧选择参加同一项目的概率是( )A、 B、 C、 D、9. 如图所示的曲边三角形可按下述方法作出:作等边 ,分别以点A,B,C为圆心,以 长为半径作 , , ,三弧所围成的图形就是一个曲边三角形.如果一个曲边三角形的周长为 ,则此曲边三角形的面积为( )
8. 某校团支部组织部分共青团员开展学雷锋志愿者服务活动,每个志愿者都可以从以下三个项目中任选一项参加:①敬老院做义工;②文化广场地面保洁;③路口文明岗值勤.则小明和小慧选择参加同一项目的概率是( )A、 B、 C、 D、9. 如图所示的曲边三角形可按下述方法作出:作等边 ,分别以点A,B,C为圆心,以 长为半径作 , , ,三弧所围成的图形就是一个曲边三角形.如果一个曲边三角形的周长为 ,则此曲边三角形的面积为( ) A、 B、 C、 D、10. 如图,在 中, ,以其三边为边向外作正方形,连结 ,作 于点M, 于点J, 于点K,交 于点L.若正方形 与正方形 的面积之比为5, ,则 的长为( )
A、 B、 C、 D、10. 如图,在 中, ,以其三边为边向外作正方形,连结 ,作 于点M, 于点J, 于点K,交 于点L.若正方形 与正方形 的面积之比为5, ,则 的长为( )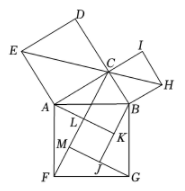 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算 的结果是.12. 某小组七位学生的中考体育测试成绩(满分40分)依次为37,40,39,37,40,38,40.则这组数据的中位数是 .13. 计算: 的结果是14. 小明为测量校园里一颗大树的高度.在树底部B所在的水平面内,将测角仪竖直放在与B相距的位置,在D处测得树顶A的仰角为.若测角仪的高度是 , 则大树的高度约为.(结果精确到.参考数据: , , )
 15. 如图,已知开口向下的抛物线与x轴交于点 , 对称轴为直线.下列四个结论:①;②;③函数的最大值为;④若关于x的方程无实数根,则.其中正确的是(填写序号).
15. 如图,已知开口向下的抛物线与x轴交于点 , 对称轴为直线.下列四个结论:①;②;③函数的最大值为;④若关于x的方程无实数根,则.其中正确的是(填写序号). 16. 如图1,在矩形中, , , E,F分别为 , 的中点,连接.如图2,将绕点A逆时针旋转角 , 使 , 连接并延长交于点H.则的长为.
16. 如图1,在矩形中, , , E,F分别为 , 的中点,连接.如图2,将绕点A逆时针旋转角 , 使 , 连接并延长交于点H.则的长为.
三、解答题
-
17. 解不等式组请按下列步骤完成解答:
( 1 )解不等式①,得_▲_;
( 2 )解不等式②,得_▲_;
( 3 )将不等式①和②的解集在数轴上表示出来;
 (1)、原不等式组的解集为_▲_.18. 已知:如图,点A、D、C、F在同一直线上, , , .
(1)、原不等式组的解集为_▲_.18. 已知:如图,点A、D、C、F在同一直线上, , , .求证: .
 19. 为了丰富学生们的课余生活,学校准备开展第二课堂,有四类课程可供选择,分别是“A.书画类、B.文艺类、C.社会实践类、D.体育类”.现随机抽取了七年级部分学生对报名意向进行调查,并根据调查结果绘制了两幅不完整的统计图,请你根据图表信息回答下列问题:
19. 为了丰富学生们的课余生活,学校准备开展第二课堂,有四类课程可供选择,分别是“A.书画类、B.文艺类、C.社会实践类、D.体育类”.现随机抽取了七年级部分学生对报名意向进行调查,并根据调查结果绘制了两幅不完整的统计图,请你根据图表信息回答下列问题: (1)、本次被抽查的学生共有名;(2)、扇形统计图中“A.书画类”所占扇形的圆心角的度数为度;(3)、请你将条形统计图补全;(4)、若该校七年级共有600名学生,请根据上述调查结果估计该校学生选择“C.社会实践类”的学生共有多少名?20. 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)、本次被抽查的学生共有名;(2)、扇形统计图中“A.书画类”所占扇形的圆心角的度数为度;(3)、请你将条形统计图补全;(4)、若该校七年级共有600名学生,请根据上述调查结果估计该校学生选择“C.社会实践类”的学生共有多少名?20. 如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.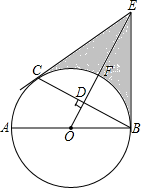 (1)、求证:BE与⊙O相切;(2)、设OE交⊙O于点F,若DF = 2,BC = , 求阴影部分的面积.21. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
(1)、求证:BE与⊙O相切;(2)、设OE交⊙O于点F,若DF = 2,BC = , 求阴影部分的面积.21. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.的顶点在格点上,仅用无刻度尺的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
( 1 )画出关于对称的线段;
( 2 )画出的中点E;
( 3 )连接并延长交于点F,直接写出的值为 ;
( 4 )在上画点G,连接 , 使.
22. 如图,灌溉车为绿化带浇水,喷水口H离地竖直高度为1.2m.可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象;把绿化带横截面抽象为矩形 , 其水平宽度 , 竖直高度.下边缘抛物线是由上边缘抛物线向左平移得到,上边抛物线最高点A离喷水口的水平距离为2m,高出喷水口0.4m,灌溉车到绿化带的距离为d(单位:m). (1)、求上边缘抛物线的函数解析式,并求喷出水的最大射程;(2)、求下边缘抛物线与x轴的正半轴交点B的坐标;(3)、要使灌溉车行驶时喷出的水能浇灌到整个绿化带,直接写出d的取值范围.23.
(1)、求上边缘抛物线的函数解析式,并求喷出水的最大射程;(2)、求下边缘抛物线与x轴的正半轴交点B的坐标;(3)、要使灌溉车行驶时喷出的水能浇灌到整个绿化带,直接写出d的取值范围.23. (1)、【问题探究】如图1,在正方形中,点E、F、G、H分别在线段、、、上,且.试猜想的值,并证明你的猜想.(2)、【知识迁移】如图2,在矩形中, , , 点E、F、G、H分别在线段、、、上,且.则求的值(用含m,n的式子表示).(3)、【拓展应用】如图3,在四边形中, , , , 点E、F分别在线段、上,且.则.24. 如图1,在平面直角坐标系中,已知二次函数 的图象经过点 , ,与y轴交于点C.
(1)、【问题探究】如图1,在正方形中,点E、F、G、H分别在线段、、、上,且.试猜想的值,并证明你的猜想.(2)、【知识迁移】如图2,在矩形中, , , 点E、F、G、H分别在线段、、、上,且.则求的值(用含m,n的式子表示).(3)、【拓展应用】如图3,在四边形中, , , , 点E、F分别在线段、上,且.则.24. 如图1,在平面直角坐标系中,已知二次函数 的图象经过点 , ,与y轴交于点C. (1)、求该二次函数的表达式;(2)、连接 ,在该二次函数图象上是否存在点P,使 ?若存在,请求出点P的坐标:若不存在,请说明理由;(3)、如图2,直线l为该二次函数图象的对称轴,交x轴于点E.若点Q为x轴上方二次函数图象上一动点,过点Q作直线 , 分别交直线l于点M,N,在点Q的运动过程中, 的值是否为定值?若是,请求出该定值;若不是,请说明理由.
(1)、求该二次函数的表达式;(2)、连接 ,在该二次函数图象上是否存在点P,使 ?若存在,请求出点P的坐标:若不存在,请说明理由;(3)、如图2,直线l为该二次函数图象的对称轴,交x轴于点E.若点Q为x轴上方二次函数图象上一动点,过点Q作直线 , 分别交直线l于点M,N,在点Q的运动过程中, 的值是否为定值?若是,请求出该定值;若不是,请说明理由.