河南省信阳市2023年九年级中考一模数学试题

试卷更新日期：2023-05-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 在数4， $- \frac{1}{4}$ ， 0，-4中，与4的和为0的数是（）

A、4 B、 $- \frac{1}{4}$ C、0 D、-4

查看试题解析
2. 如图是一个正方体的表面展开图，则原正方体中与“快”字所在的面相对的面上标的字是（）

A、我 B、运 C、动 D、乐

查看试题解析
3. 如图，直线a、b相交于点O，如果∠1+∠2=110°，那么∠3的度数是（）

A、125° B、110° C、70° D、55°

查看试题解析
4. 下列计算中一定正确的是（）

A、a²+a³＝a⁵ B、a²•a³＝a⁶ C、（ab）²＝ab² D、（-a²）³＝-a⁶

查看试题解析
5. 如图，点O为菱形ABCD的对角线AC，BD的交点，过点C作CE⊥AB于点E，连接OE，若OD＝3，OE＝2，则菱形ABCD的面积为（）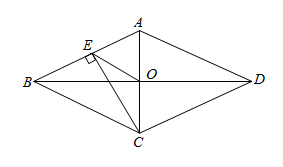

A、6 B、12 C、18 D、24

查看试题解析
6. 一元二次方程 $x^{2} + 4 = 2 x$ 根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、只有一个实数根

查看试题解析
7. 小杭同学将自己前7次体育模拟测试成绩（单位：分）统计如表，第8次测试的成绩为a分，若这8次成绩的众数不止一个，则a的值为（）
次数
第1次
第2次
第3次
第4次
第5次
第6次
第7次
成绩
27
28
30
28
29
29
28

A、27 B、28 C、29 D、30

查看试题解析
8. 电影《我和我的祖国》是由陈凯歌担任总导演，反映小人物见证大时代，献礼新中国成立70周年的献礼片，于2019年9月30日在中国大陆上映，到目前为止，影片累计票房达28.40亿元，用科学记数法表示 28.40亿元为（）.

A、 $28.4 \times 1 0^{8}$ 元 B、 $2.84 \times 1 0^{8}$ 元 C、 $0.284 \times 1 0^{7}$ 元 D、 $2.84 \times 1 0^{9}$ 元

查看试题解析
9. 如图，在 $△ A B C$ 中，顶点A在x轴的负半轴上， $B (0 ， 2)$ ， $C (\sqrt{5} ， 2)$ ， $A B = B C$ ，将 $△ A B C$ 绕点A逆时针旋转，每秒旋转90°，则第2022秒旋转结束时，点B的坐标为（）

A、 $(- 2 ， - 2)$ B、 $(1 ， - 1)$ C、 $(- 3 ， 1)$ D、 $(0 ， 2)$

查看试题解析
10. 如图1，在 $▱ A B C D$ 中，点M，N同时从点B出发，点M以 $\sqrt{3} c m / s$ 的速度沿B→A→D→C匀速运动到点C，点N以1cm/s的速度沿BC匀速运动到点C，当其中一点到达终点时，另一点也随之停止运动.设点M的运动路程长为 $x (c m)$ ， $△ B M N$ 的面积为 $y (c m^{2})$ ， y与x的函数图象如图2所示，当运动时间为 $\frac{8}{3} s$ 时， $△ B M N$ 的面积是（） $c m^{2}$ .

A、 $\frac{7}{4}$ B、 $\frac{3}{2}$ C、 $\frac{3 \sqrt{3}}{2}$ D、 $\frac{4 \sqrt{3}}{3}$

查看试题解析

二、填空题

11. 请写出一个图象经过第一、二、四象限且与y轴交于点（0，1）的一次函数的解析式 .

查看试题解析
12. 不等式组 ${\begin{array}{l} x - 1 \leq 0 \\ \frac{x - 2}{2} < x \end{array}$ 的解集是.

查看试题解析
13. 某校欲从初三级部3名女生，2名男生中任选两名学生代表学校参加全市举办的“中国梦•青春梦”演讲比赛，则恰好选中一男一女的概率是．

查看试题解析
14. 如图，在▱ $A B C D$ 中， $A B = 2$ ，以点C为圆心， $C D$ 长为半径画弧，与 $B C$ ， $A D$ 分别交于点E，F，过点F作 $F G ⊥ B C$ 于点G，若 $F G = \sqrt{3}$ ，则图中阴影部分的面积为.

查看试题解析
15. 如图，△ABC中，∠ACB＝90°，∠A＝30°，BC＝1，CD是△ABC的中线，E是AC上一动点，将△AED沿ED折叠，点A落在点F处，EF线段CD交于点G，若△CEG是直角三角形，则CE＝.

查看试题解析

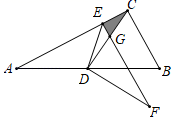
三、解答题

16.

(1)、计算： $\sqrt[3]{- 8} + {(\frac{1}{3})}^{- 1} + {(π - 3)}^{0}$ ；

(2)、化简： $(\frac{1}{x - 1} - 1) \div \frac{x - 2}{x^{2} - x}$ .

查看试题解析
17. 金秋十月，中国共产党第二十次全国代表大会在北京召开.这是在全党全国各族人民迈向全面建设社会主义现代化国家的新征程，向第二个百年奋斗目标进军的关键时刻召开的一次十分重要的大会.某校推出“喜迎二十大”的党史知识竞赛活动，现从八年级和九年级参与竞赛的学生中各随机选出20名同学的成绩进行分析.将学生竞赛成绩分为A、B、C、D四个等级.分别是：A. $90 \leq x < 100$ ， B. $80 \leq x < 90$ ， C. $70 \leq x < 80$ ， D. $0 \leq x < 70$ .
八年级学生的竞赛成绩为：99，98，95，94，91，90，89，87，87，87，87，84，84，83，82，81，81，79，70，58；
九年级等级B的学生成绩为：89，89，88，87，85，83，82；
A、B、C、D等级的扇形统计图如下.两组数据的平均数、中位数、众数、方差如下表所示
学生
平均数
中位数
众数
方差
八年级
$85.3$
$87$
a
$83.71$
九年级
$85.3$
b
$91$
$81.76$
根据以上信息，解答下列问题：

(1)、直接写出a，b，m的值；

(2)、根据以上数据.你认为在此次知识竞赛中，哪个年级的成绩更好？请说明理由（一条理由即可）；

(3)、若八，九年级各有 $600$ 名学生参赛，请估计两个年级参赛学生中成绩优秀（大或等于 $90$ 分）的学生共有多少人？

查看试题解析
18. 如图，在平面直角坐标系xOy中，一次函数 $y = - x + 5$ 的图象与反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象相交于A，B两点，与x轴相交于点C，连接OB，且 $△ B O C$ 的面积为 $\frac{5}{2}$ ．

(1)、求反比例函数的表达式；

(2)、将直线AB向下平移，若平移后的直线与反比例函数的图象只有一个交点，试说明直线AB向下平移了几个单位长度？

查看试题解析
19. 某数学学习小组利用卷尺和自制的测角仪测量魁星阁顶端距离地面的高度，如图所示，他们在地面一条水平步道 $F B$ 上架设测角仪，先在点F处测得魁星阁顶端A的仰角是26°，朝魁星阁方向走20米到达G处，在G处测得魁星阁顶端A的仰角是45°.若测角仪 $C F$ 和 $D G$ 的高度均为 $1.5$ 米，求魁星阁顶端距离地面的高度（图中 $A B$ 的值）.（参考数据： $s i n 26 ° \approx 0.44$ ， $c o s 24 ° \approx 0.90$ ， $t a n 26 ° \approx 0.49$ ， $\sqrt{2} \approx 1.41$ ，结果精确到 $0.1$ 米）

查看试题解析
20. 某文具店准备购甲、乙两种水笔进行销售，每支进价和利润如表：

甲水笔
乙水笔
每支进价（元）
a
$a + 5$
每支利润（元）
2
3
已知花费400元购进甲水笔的数量和花费800元购进乙水笔的数量相等.

(1)、求甲，乙两种水笔每支进价分别为多少元.

(2)、若该文具店准备拿出2000元全部用来购进这两种水笔，考虑顾客需求，要求购进甲种水笔的数量不超过乙种水笔数量的4倍，问该文具店如何进货能使利润最大，最大利润是多少元.

查看试题解析
21. 现要修建一条隧道，其截面为抛物线型，如图所示，线段 $O E$ 表示水平的路面，以O为坐标原点，以 $O E$ 所在直线为x轴，以过点O垂直于x轴的直线为y轴，建立平面直角坐标系.根据设计要求： $O E = 10 m$ ，该抛物线的顶点P到 $O E$ 的距离为 $9 m$ .

(1)、求满足设计要求的抛物线的函数表达式；

(2)、现需在这一隧道内壁上安装照明灯，如图所示，即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到 $O E$ 的距离均为 $6 m$ ，求点A、B的坐标.

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 10$ ， $B C = 6$ .用直尺和圆规按下列步骤作图：
①以点B为圆心，适当的长为半径画弧，分别交边BC，AB于点D，E；
②分别以点D，E为圆心，大于 $\frac{1}{2} D E$ 的长为半径画弧，两弧交于点P；
③作射线BP，交边AC于点O；
④以点O为圆心，OC的长为半径画 $⊙ O$ ，交射线BP于点F，G（点G在线段OB上），连接CF，CG.

(1)、求证：AB是 $⊙ O$ 的切线；

(2)、求 $⊙ O$ 的半径长；

(3)、求 $\frac{C G}{C F}$ 的值.

查看试题解析
23. 向题情境：数学活动课上，老师组织同学们以“正方形”为主题开展数学活动.

(1)、动手实践：如图①，已知正方形纸片 $A B C D$ ，勤奋小组将正方形纸片沿过点A的直线折叠.使点B落在正方形 $A B C D$ 的内部，点B的对应点为点M，折痕为 $A E$ ，再将纸片沿过点A的直线折叠，使 $A D$ 与 $A M$ 重合，折痕为 $A F$ ，易知点E、M、F共线，则 $∠ E A F =$ 度.

(2)、拓展应用：如图②，腾飞小组在图①的基础上进行如下操作：将正方形纸片沿 $E F$ 继续折叠，使得点C的对应点为点N，他们发现，当点E的位置不同时，点N的位置也不同，当点E在 $B C$ 边的某一位置时，点N恰好落在折痕 $A E$ 上.

①则 $∠ C F E =$ 度.

②设 $A M$ 与 $N F$ 的交点为点P，运用（1）、（2）操作所得结论，求证： $△ A N P ≌ △ F N E$ .

(3)、解决问题：在图②中，若 $A B = 3$ ，请直接写出线段 $M P$ 的长.

查看试题解析

次数	第1次	第2次	第3次	第4次	第5次	第6次	第7次
成绩	27	28	30	28	29	29	28

学生	平均数	中位数	众数	方差
八年级	$85.3$	$87$	a	$83.71$
九年级	$85.3$	b	$91$	$81.76$

	甲水笔	乙水笔
每支进价（元）	a	$a + 5$
每支利润（元）	2	3