河南省洛阳市宜阳县2023年九年级第一次学情诊断数学试题

试卷更新日期：2023-05-09 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{24}$ B、 $\sqrt{15}$ C、 $\sqrt{\frac{5}{3}}$ D、 $\sqrt{0.3}$

查看试题解析
2. “抛一枚均匀硬币，落地后正面朝上”这一事件是（　　）

A、必然事件 B、随机事件 C、确定事件 D、不可能事件

查看试题解析
3. 如图，在平面直角坐标系中，将 $△ O A B$ 以原点O为位似中心放大后得到 $△ O C D$ ，若 $B (0 ， 1)$ ， $D (0 ， 3)$ ，则 $△ O A B$ 与 $△ O C D$ 的面积的比是（）

A、1：2 B、1：3 C、1：9 D、9：1

查看试题解析
4. 将抛物线 $y = 2 x^{2} -1$ 向左平移2个单位长度，再向下平移3个单位长度，得到的抛物线的解析式为（）

A、 $y = 2 {(x + 2)}^{2} - 4$ B、 $y = {(x + 2)}^{2} -4$ C、 $y = 2 {(x - 2)}^{2} -4$ D、 $y = 2 {(x - 2)}^{2} - 3$

查看试题解析
5. 如图，有一张矩形纸片，长10cm，宽6cm，在它的四角各剪去一个同样的小正方形，然后折叠成一个无盖的长方体纸盒.若纸盒的底面（图中阴影部分）面积是32cm² ，求剪去的小正方形的边长.设剪去的小正方形边长是xcm，根据题意可列方程为（）

A、10×6-4×6x=32 B、（10-2x）（6-2x）=32 C、（10-x）（6-x）=32 D、10×6-4x²=32

查看试题解析
6. 如图，AB是⊙O的直径，∠C=15°，则∠BAD的度数为（）

A、45° B、55° C、60° D、75°

查看试题解析
7. 如图，在 $△ A B C$ 中， $B C = 12$ ， $D 、 E$ 分别是 $A B ， A C$ 的中点，F是 $D E$ 上一点， $D F = 1$ ，连接 $A F 、 C F$ ，若 $∠ A F C = 90 °$ ，则 $A C$ 的长度为（）

A、10 B、12 C、13 D、16

查看试题解析
8. 对于一元二次方程 $x^{2} - 3 x + c = 0$ ，当 $c = \frac{9}{4}$ 时，方程有两个相等的实数根.若将c的值在 $\frac{9}{4}$ 的基础上减小，则此时方程根的情况是（）

A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定

查看试题解析
9. 如图，在△ABC中，∠ABC＝∠C，将△ABC绕点B逆时针旋转得△DBE，点E在AC上，若ED＝3，EC＝1，则EB＝（）

A、 $\sqrt{3}$ B、 $\frac{3}{2}$ C、 $\frac{\sqrt{3} + 1}{2}$ D、2

查看试题解析
10. 如图，在 $△ A B C$ 中， $A B = 10 c m$ ， $A C = 8 c m$ ， $B C = 6 c m$ ，直线l经过点A，且垂直于 $A B$ .将直线l从点A处开始，沿 $A B$ 方向以 $1 c m / s$ 的速度向点B平移，平移过程中与 $A B$ 交于点M，与 $A C$ 或 $C B$ 交于N，当直线l平移到点B时停止.若直线l的平移时间是 $x (s)$ ，平移过程中 $△ A M N$ 的面积是 $y (c m^{2})$ ，则y与x之间函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

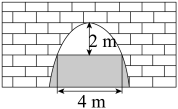
11. 若代数式 $\frac{2}{\sqrt{2 x - 6}}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
12. 某商场举行有奖竞猜活动，有A，B，C，D四个问题，其中A，B为体育类问题，C，D为文化类问题，小华从四个问题中不重复地选择两个，则两个问题类型相同的概率为.

查看试题解析
13. 设 $α$ ， $β$ 是一元二次方程 $x^{2} + x - 6 = 0$ 的两个根，则 $\frac{1}{α} + \frac{1}{β} =$ .

查看试题解析
14. 如图是一个横断面为抛物线形状的拱桥，当拱顶（拱桥洞的最高点）离水面 $2 m$ 时，水面宽 $4 m$ ，当水面下降 $2 m$ 时，水面的宽度为m.

查看试题解析
15. 将三角形纸片(△ABC)按如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF.已知AB＝AC＝3，BC＝4，若以点B′，F，C为顶点的三角形与△ABC相似，则BF的长度是.

查看试题解析

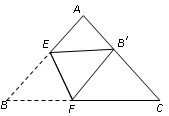
三、解答题

16.

(1)、计算： $2 c o s^{2} 45 ° - 1 + t a n 30 ° \times t a n 60 °$ ；

(2)、解方程： $x^{2} - 8 x + 11 = 0$ .

查看试题解析
17. 已知关于x的一元二次方程 $x^{2} - (2 k + 1) x + 2 k = 0$ .

(1)、求证：方程总有两个实数根；

(2)、若该方程有一个根大于2，求k的取值范围.

查看试题解析
18. 为庆祝中国共青团成立100周年，某校开展四项活动： $A$ 项参观学习， $B$ 项团史宣讲， $C$ 项经典诵读， $D$ 项文学创作，要求每名学生在规定时间内必须且只能参加其中一项活动.该校从全体学生中随机抽取部分学生，调查他们参加活动的意向，将收集的数据整理后，绘制成如下两幅不完整的统计图.

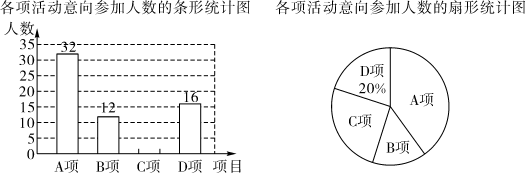(1)、本次调查的样本容量是， $B$ 项活动所在扇形的圆心角的大小是，条形统计图中 $C$ 项活动的人数是；

(2)、若该校约有2000名学生，请估计其中意向参加“参观学习”活动的人数.

查看试题解析
19. 如图，在 $△ A B C$ 中，点D，G分别在边 $A B ， B C$ 上， $∠ A C D = ∠ B$ ， $A G$ 与 $C D$ 交于点F.

(1)、求证： $A C^{2} = A D \cdot A B$ ；

(2)、若 $\frac{A D}{A C} = \frac{D F}{C G}$ ，求证： $A G$ 平分 $∠ B A C$ .

查看试题解析
20. 为落实国家精准扶贫政策，某地扶贫办决定帮助扶贫对象推销当地特色农产品，该农产品成本价为18元每千克，销售单价y（元）与每天销售量x（千克）（x为正整数）之间满足如图所示的函数关系，其中销售单价不得低于成本价.

(1)、求出y与x之间所满足的函数关系式，并写出自变量x的取值范围；

(2)、当销售量为多少时，获利最大？最大利润是多少？

查看试题解析
21. 应天门是隋唐洛阳城中轴建筑群上著名的“七天建筑”之一，是古代举行重大国事庆典与外交活动的重要场所.
问题提出：如何测量应天门东阙楼的高度？
方案设计：如图，某数学课题研究小组通过调查研究和实地测量，他们在B处测得东阙楼楼顶A的仰角为 $41 °$ ，沿 $B C$ 向前走了 $20 m$ 至点C处（ $B ， C ， D$ 三点在同一水平线上），测得东阙楼楼顶A的仰角为 $60 °$ .
问题解决：根据上述方案和数据，求应天门东阙楼 $A D$ 的高度.（结果精确到 $1 m$ ，参考数据： $s i n 41 ° \approx 0.66$ ， $c o s 41 ° \approx 0.75$ ， $t a n 41 ° \approx 0.87$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析
22. 如图，抛物线 $y = x^{2} - 6 x + c$ 与x轴交于点 $A (x_{1} ， 0)$ ， $B (x_{2} ， 0)$ ，点A在点B的右侧，与y轴交于点C.

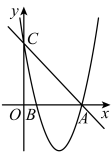(1)、若直线AC的解析式为 $y = - x + 5$ ，求抛物线的解析式；

(2)、在（1）的条件下，过点B的直线与抛物线 $y = x^{2} - 6 x + c$ 交于另一点P.若直线AC与直线BP平行，求点P的坐标；

(3)、点 $M (- 1 ， - 4)$ ， $N (6 ， - 4)$ 为平面直角坐标系内两点，连结MN.若抛物线与线段MN只有一个公共点，直接写出c的取值范围.

查看试题解析
23. 在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的有关圆的一个引理：如图1， $A B$ 是 $⊙ O$ 的弦，点P在 $⊙ O$ 上， $P C ⊥ A B$ 于点C，点D在弦 $A B$ 上且 $A C = C D$ ，在 $\overset{⌢}{P B}$ 上取一点Q， $\overset{⌢}{P Q} = \overset{⌢}{P A}$ ，连接 $B Q$ ，则 $B Q = B D$ .

(1)、如图2，小亮尝试说明 $B Q = B D$ ，于是他连接了 $P A$ ， $P D$ ， $P Q$ ， $D Q$ .请你帮助他完成下列证明.
①求证： $∠ P Q B = ∠ P D B$ ；
②求证： $B Q = B D$ .

(2)、如图3，将材料中的“弦 $A B$ ”改为“直径 $A B$ ”，作直线l与 $⊙ O$ 相切于点Q.过点P作 $P G ⊥$ 直线l于点G，其余条件不变，连接 $P A$ ， $P Q$ .若 $P G = 2$ ， $B Q = 6$ ，求 $⊙ O$ 的半径 $O A$ 的长

查看试题解析