专题04 立体几何-【大题精做】冲刺2023年高考大题突破训练
试卷更新日期:2023-05-09 类型:高考模拟
一、解答题
-
1. 已知三棱柱棱长均为 , 且 , .
 (1)、求证:平面平面;(2)、求平面与平面所成夹角的余弦值.2. 如图,在三棱台中,.
(1)、求证:平面平面;(2)、求平面与平面所成夹角的余弦值.2. 如图,在三棱台中,. (1)、求证:平面平面;(2)、若四面体的体积为2,求二面角的余弦值.3. 如图,在四棱锥中,平面平面ABCD,平面平面ABCD.
(1)、求证:平面平面;(2)、若四面体的体积为2,求二面角的余弦值.3. 如图,在四棱锥中,平面平面ABCD,平面平面ABCD. (1)、求证:平面ABCD;(2)、设 , , , 平面PBC与平面PCD的夹角的余弦值为 , 求BC的长.4. 如图,在圆台中,圆的半径是1,圆的半径是2,高是 , 圆是的外接圆, , PC是圆台的一条母线.
(1)、求证:平面ABCD;(2)、设 , , , 平面PBC与平面PCD的夹角的余弦值为 , 求BC的长.4. 如图,在圆台中,圆的半径是1,圆的半径是2,高是 , 圆是的外接圆, , PC是圆台的一条母线.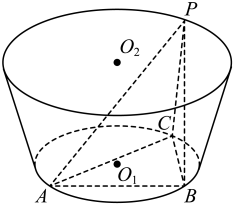 (1)、求三棱锥体积的最大值;(2)、当时,求平面PAC与平面PBC的锐二面角的余弦值.5. 如图,多面体是由棱长为3的正方体沿平面截去一角所得到,在棱上取一点E,过点 , C,E的平面交棱于点F.
(1)、求三棱锥体积的最大值;(2)、当时,求平面PAC与平面PBC的锐二面角的余弦值.5. 如图,多面体是由棱长为3的正方体沿平面截去一角所得到,在棱上取一点E,过点 , C,E的平面交棱于点F. (1)、求证:;(2)、若 , 求点E到平面的距离以及与平面所成角的大小.6. 如图,在正三棱柱中,已知 , 是的中点.
(1)、求证:;(2)、若 , 求点E到平面的距离以及与平面所成角的大小.6. 如图,在正三棱柱中,已知 , 是的中点. (1)、求直线与所成的角的大小;(2)、求证:平面平面 , 并求点到平面的距离.7. 如图,三角形与梯形所在的平面互相垂直, , , , , , 、分别为、的中点.
(1)、求直线与所成的角的大小;(2)、求证:平面平面 , 并求点到平面的距离.7. 如图,三角形与梯形所在的平面互相垂直, , , , , , 、分别为、的中点.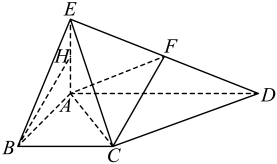 (1)、求证:平面;(2)、求平面与平面所成锐二面角的余弦值.8. 如图,正三棱柱中, , 点M为的中点.
(1)、求证:平面;(2)、求平面与平面所成锐二面角的余弦值.8. 如图,正三棱柱中, , 点M为的中点. (1)、在棱上是否存在点Q,使得AQ⊥平面?若存在,求出的值;若不存在,请说明理由:(2)、求点C到平面的距离.9. 在四棱锥中,平面平面 , , 为的中点.
(1)、在棱上是否存在点Q,使得AQ⊥平面?若存在,求出的值;若不存在,请说明理由:(2)、求点C到平面的距离.9. 在四棱锥中,平面平面 , , 为的中点. (1)、求证:;(2)、若 , , , , 点在棱上,直线与平面所成角为 , 求点到平面的距离.10. 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD, , , 点E在线段AB上,且 .
(1)、求证:;(2)、若 , , , , 点在棱上,直线与平面所成角为 , 求点到平面的距离.10. 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥平面ABCD, , , 点E在线段AB上,且 . (1)、求证:CE⊥平面PBD;(2)、求二面角P-CE-A的余弦值.11. 如图,在圆锥中,是底面的直径,是底面圆周上的一点,且 , , , 是的中点.
(1)、求证:CE⊥平面PBD;(2)、求二面角P-CE-A的余弦值.11. 如图,在圆锥中,是底面的直径,是底面圆周上的一点,且 , , , 是的中点. (1)、求证:平面平面;(2)、求二面角的余弦值.12. 如图,在五面体ABCDEF中,FA⊥平面ABCD, , 若.
(1)、求证:平面平面;(2)、求二面角的余弦值.12. 如图,在五面体ABCDEF中,FA⊥平面ABCD, , 若. (1)、求五面体ABCDEF的体积;(2)、若M为EC的中点,求证:平面平面AMD.13. 如图,平面五边形中,△是边长为2的等边三角形, , , , 将△沿翻折,使点翻折到点 .
(1)、求五面体ABCDEF的体积;(2)、若M为EC的中点,求证:平面平面AMD.13. 如图,平面五边形中,△是边长为2的等边三角形, , , , 将△沿翻折,使点翻折到点 . (1)、证明:;(2)、若 , 求直线与平面所成角的正弦值.14. 如图,在三棱锥中,为的内心,直线与交于 , , .
(1)、证明:;(2)、若 , 求直线与平面所成角的正弦值.14. 如图,在三棱锥中,为的内心,直线与交于 , , .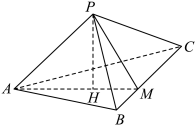 (1)、证明:平面平面;(2)、若 , , , 求二面角的余弦值.15. 圆柱中,四边形为过轴的截面, , , 为底面圆的内接正三角形, .
(1)、证明:平面平面;(2)、若 , , , 求二面角的余弦值.15. 圆柱中,四边形为过轴的截面, , , 为底面圆的内接正三角形, . (1)、证明:平面;(2)、求平面与平面所成角的正弦值.16. 在三棱锥中,底面为等腰直角三角形,.
(1)、证明:平面;(2)、求平面与平面所成角的正弦值.16. 在三棱锥中,底面为等腰直角三角形,. (1)、求证:;(2)、若 , 求平面与平面夹角的余弦值.17. 如图,在几何体中,菱形所在的平面与矩形所在的平面互相垂直.
(1)、求证:;(2)、若 , 求平面与平面夹角的余弦值.17. 如图,在几何体中,菱形所在的平面与矩形所在的平面互相垂直. (1)、若为线段上的一个动点,证明:∥平面(2)、若 , , 直线与平面所成角的正弦值为 , 求点到平面的距离.18. 已知三棱锥中,△是边长为3的正三角形,与平面所成角的余弦值为 .
(1)、若为线段上的一个动点,证明:∥平面(2)、若 , , 直线与平面所成角的正弦值为 , 求点到平面的距离.18. 已知三棱锥中,△是边长为3的正三角形,与平面所成角的余弦值为 . (1)、求证:;(2)、求二面角的平面角的正弦值.19. 如图,已知点P在圆柱的底面圆O的圆周上,AB为圆O的直径,圆柱的表面积为 , , .
(1)、求证:;(2)、求二面角的平面角的正弦值.19. 如图,已知点P在圆柱的底面圆O的圆周上,AB为圆O的直径,圆柱的表面积为 , , . (1)、求直线与平面所成角的大小;(2)、求点到平面的距离.20. 如图,四棱锥的底面为矩形, , , , 平面平面 . 是的中点,是上一点,且平面 .
(1)、求直线与平面所成角的大小;(2)、求点到平面的距离.20. 如图,四棱锥的底面为矩形, , , , 平面平面 . 是的中点,是上一点,且平面 .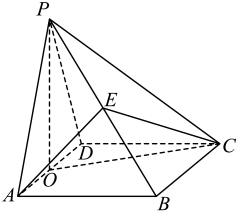 (1)、求的值;(2)、求直线与平面所成角的正弦值.21. 如图,在四面体中,为的重心, , 分别在棱 , 上,平面平面.
(1)、求的值;(2)、求直线与平面所成角的正弦值.21. 如图,在四面体中,为的重心, , 分别在棱 , 上,平面平面. (1)、求的值;(2)、若平面 , , 且 , 求平面与平面的夹角的大小.22. 已知正三棱柱中,侧棱长为 , 底面边长为2,D为AB的中点.
(1)、求的值;(2)、若平面 , , 且 , 求平面与平面的夹角的大小.22. 已知正三棱柱中,侧棱长为 , 底面边长为2,D为AB的中点. (1)、证明:;(2)、求二面角的大小;(3)、求直线CA与平面所成角的正弦值.23. 如图,在多面体中,四边形和四边形均是等腰梯形,底面为矩形,与的交点为 , 平面 , 且与底面的距离为 ,
(1)、证明:;(2)、求二面角的大小;(3)、求直线CA与平面所成角的正弦值.23. 如图,在多面体中,四边形和四边形均是等腰梯形,底面为矩形,与的交点为 , 平面 , 且与底面的距离为 , (1)、求证:平面;(2)、在线段上是否存在一点 , 使得与平面所成角的正弦值为 . 若存在,请确定点的位置;若不存在,请说明理由.24. 如图,在四棱锥中,底面 , , , , , .
(1)、求证:平面;(2)、在线段上是否存在一点 , 使得与平面所成角的正弦值为 . 若存在,请确定点的位置;若不存在,请说明理由.24. 如图,在四棱锥中,底面 , , , , , . (1)、证明:平面平面;(2)、求与平面所成角的余弦值.25. 如图1,平面图形是一个直角梯形,其中 , 是上一点,且.将沿着折起使得平面平面 , 连接 , 分别是的中点,如图2.
(1)、证明:平面平面;(2)、求与平面所成角的余弦值.25. 如图1,平面图形是一个直角梯形,其中 , 是上一点,且.将沿着折起使得平面平面 , 连接 , 分别是的中点,如图2. (1)、证明:在图2中四点共面,且平面平面;(2)、在图2中,若是线段上一个动点,当直线与平面所成角的正弦值取得最大值时,求的长.26. 如图,在四棱锥中,底面是正方形, , , 二面角的大小为 .
(1)、证明:在图2中四点共面,且平面平面;(2)、在图2中,若是线段上一个动点,当直线与平面所成角的正弦值取得最大值时,求的长.26. 如图,在四棱锥中,底面是正方形, , , 二面角的大小为 . (1)、证明:平面平面;(2)、求与平面所成角的正弦值.27. 如图所示的在多面体中, , 平面平面 , 平面平面 , 点分别是中点.
(1)、证明:平面平面;(2)、求与平面所成角的正弦值.27. 如图所示的在多面体中, , 平面平面 , 平面平面 , 点分别是中点. (1)、证明:平面平面;(2)、若 , 求平面和平面夹角的余弦值.28. 如图所示,在四棱锥中, , , , .
(1)、证明:平面平面;(2)、若 , 求平面和平面夹角的余弦值.28. 如图所示,在四棱锥中, , , , . (1)、证明:;(2)、求直线BC与平面PCD所成角的余弦值.29. 如图,已知矩形是圆柱的轴截面,是的中点,直线与下底面所成角的正切值为 , 矩形的面积为12,为圆柱的一条母线(不与重合).
(1)、证明:;(2)、求直线BC与平面PCD所成角的余弦值.29. 如图,已知矩形是圆柱的轴截面,是的中点,直线与下底面所成角的正切值为 , 矩形的面积为12,为圆柱的一条母线(不与重合). (1)、证明:;(2)、当三棱锥的体积最大时,求二面角的正弦值.30. 如图,四棱锥的底面是正方形,点P,Q在侧棱上,E是侧棱的中点.
(1)、证明:;(2)、当三棱锥的体积最大时,求二面角的正弦值.30. 如图,四棱锥的底面是正方形,点P,Q在侧棱上,E是侧棱的中点. (1)、若 , 证明:BE∥平面;(2)、若每条侧棱的长都是底面边长的倍,从下面两个条件中选一个,求二面角的大小.
(1)、若 , 证明:BE∥平面;(2)、若每条侧棱的长都是底面边长的倍,从下面两个条件中选一个,求二面角的大小.①平面;②P为的中点.
注:如果选择多个条件分别解答,按第一个解答计分.
31. 如图1,四边形ABCD是等腰梯形,E,F分别是AD,BC的中点, . 将四边形ABFE沿着EF折起到四边形处,使得 , 如图2,G在上,且 . (1)、证明:平面DFG;(2)、求平面DFG与平面夹角的余弦值32. 如图,在三棱柱中,侧面和侧面均为正方形,为棱的中点.
(1)、证明:平面DFG;(2)、求平面DFG与平面夹角的余弦值32. 如图,在三棱柱中,侧面和侧面均为正方形,为棱的中点. (1)、证明:平面平面;(2)、若直线与平面所成角为30°,求平面与平面夹角的余弦值.33. 如图,已知三棱柱 , , , 为线段上的动点,.
(1)、证明:平面平面;(2)、若直线与平面所成角为30°,求平面与平面夹角的余弦值.33. 如图,已知三棱柱 , , , 为线段上的动点,. (1)、求证:平面平面;(2)、若 , D为线段的中点, , 求与平面所成角的余弦值.34. 如图,在斜三棱柱中,底面是边长为2的正三角形,侧面为菱形,已知 , .
(1)、求证:平面平面;(2)、若 , D为线段的中点, , 求与平面所成角的余弦值.34. 如图,在斜三棱柱中,底面是边长为2的正三角形,侧面为菱形,已知 , . (1)、当时,求三棱柱的体积;(2)、设点P为侧棱上一动点,当时,求直线与平面所成角的正弦值的取值范围.35. 如图所示,在四棱锥中,底面是等腰梯形, , . 平面平面 , 为的中点, , , E,F,G分别为 , , 的中点.
(1)、当时,求三棱柱的体积;(2)、设点P为侧棱上一动点,当时,求直线与平面所成角的正弦值的取值范围.35. 如图所示,在四棱锥中,底面是等腰梯形, , . 平面平面 , 为的中点, , , E,F,G分别为 , , 的中点. (1)、求证:平面平面;(2)、求平面与平面所成锐二面角的正切值.36. 如图,在三棱柱中,四边形是菱形, , , , , 分别为 , 的中点,且平面平面 .
(1)、求证:平面平面;(2)、求平面与平面所成锐二面角的正切值.36. 如图,在三棱柱中,四边形是菱形, , , , , 分别为 , 的中点,且平面平面 . (1)、求证:;(2)、求直线与平面所成角的正弦值.37. 如图,在四棱锥中,底面为直角梯形,∥.
(1)、求证:;(2)、求直线与平面所成角的正弦值.37. 如图,在四棱锥中,底面为直角梯形,∥. (1)、证明:平面平面;(2)、求平面与平面所成锐二面角的余弦值.
(1)、证明:平面平面;(2)、求平面与平面所成锐二面角的余弦值.


