广东省广州市花都区2022-2023学年七年级下学期期中数学试题

试卷更新日期：2023-05-09 类型：期中考试

进入出卷网下载

一、单选题

1. -2的绝对值等于（）

A、2 B、-2 C、2或-2 D、 $\frac{1}{2}$

查看试题解析
2. 下列图形中，能通过某个基本图形经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 以下实数中，属于无理数的是（）

A、0.7 B、 $\frac{1}{2}$ C、 $\sqrt{2}$ D、 $\sqrt{9}$

查看试题解析
4. 下列几组解中，二元一次方程 $2 x + 3 y = 0$ 的解是（）

A、 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ C、 ${\begin{array}{l} x = - 3 \\ y = - 2 \end{array}$ D、 ${\begin{array}{l} x = 2 \\ y = 3 \end{array}$

查看试题解析
5. 如图，直线a，b被直线c所截，则 $∠ 1$ 的同位角是（）

A、 $∠ 2$ B、 $∠ 3$ C、 $∠ 4$ D、 $∠ 5$

查看试题解析
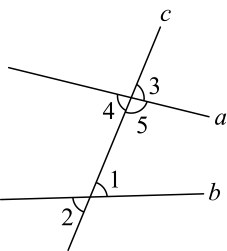6. 在平面直角坐标系中，点 $P (m ， n)$ 满足 $(m + 3)^{2} + \sqrt{4 - n} = 0$ ，则点P的坐标是（）

A、 $(3 ， 4)$ B、 $(4 ， 3)$ C、 $(- 3 ， 4)$ D、 $(4 ， - 3)$

查看试题解析
7. 如图，数轴被墨迹污染了，被覆盖的数不可能是（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{6}$ D、 $\sqrt{7}$

查看试题解析
8. 如图，把长方形 $A B C D$ 沿 $E F$ 折叠后，点D，C分别落在 $D^{'}$ ， $C^{'}$ 的位置．若 $∠ D^{'} E F = 65 °$ ，则 $∠ C^{'} F B$ 是（）

A、 $45 °$ B、 $50 °$ C、 $60 °$ D、 $65 °$

查看试题解析
9. 丫丫从学校骑自行车出发到图书馆，中途因道路施工步行了一段路，一共用了1.5小时到达图书馆．她骑车的平均速度是 $15 k m / h$ ，步行的平均速度是 $5 k m / h$ ，路程全长 $20 k m$ ，设丫丫骑车的时间是x小时，步行的时间是y小时．则可列方程为（）

A、 ${\begin{array}{l} x + y = 3 \\ 15 x + 5 y = 20 \end{array}$ B、 ${\begin{array}{l} x + y = 1.5 \\ 15 x + 5 y = 20 \end{array}$ C、 ${\begin{array}{l} x + y = 1.5 \\ 5 x + 15 y = 20 \end{array}$ D、 ${\begin{array}{l} x + y = 3 \\ 5 x + 15 y = 20 \end{array}$

查看试题解析
10. 如图，在平面直角坐标系中，动点P从原点出发，按图中箭头的所示方向连续运动，依次得到点 $P_{1} (1 ， 1)$ ， $P_{2} (2 ， 0)$ ， $P_{3} (3 ， - 2)$ ， $P_{4} (4 ， 0)$ ， $P_{5} (5 ， 1)$ ， ……，则点 $P_{2023}$ 的坐标是（）

A、 $(2022 ， 1)$ B、 $(2023 ， 1)$ C、 $(2023 ， 0)$ D、 $(2023 ， - 2)$

查看试题解析

二、填空题

11. 在平面直角坐标系中，点 $(- 5 ， - 1)$ 在第象限．

查看试题解析
12. 计算： $2 (4 x - 1) =$ ．

查看试题解析
13. 实数a，b在数轴上的位置如图所示，比较大小： $a$ $- b$ （填“ $>$ ， $=$ ， $<$ ”）

查看试题解析
14. 若 $- 4 a^{2 m} b^{3}$ 与 $5 a^{6} b^{n + 1}$ 是同类项，则 $m + n =$ ．

查看试题解析
15. 一副三角尺的摆放位置如图所示，则 $∠ 1$ 的度数是．

查看试题解析
16. 定义新运算：对于任意实数a、b，都有 $a \otimes b = (a + b) (a - b)$ ，比如： $6 \otimes 2 = (6 + 2) (6 - 2) = 8 \times 4 = 32$ ，则 $9 \otimes (4 \otimes 3) =$ ．

查看试题解析

三、解答题

17. 计算： $5 \sqrt{3} + (\sqrt{4} + 2 \sqrt{3})$ ．

查看试题解析
18. 解方程组： ${\begin{array}{l} x + y = 5 \\ 2 x - y = 4 \end{array}$ ．

查看试题解析
19. 已知：如图 $A B ∥ C D$ ， $C B ∥ D E$ ．求证： $∠ B + ∠ D = 180 °$ ．
证明：∵ $A B ∥ C D$ （已知）
∴ $∠ B =$       ▲      （两直线平行，内错角相等）
∵ $C B ∥ D E$ （已知）
∴ $∠ C + ∠ D = 180 °$ （          ）
∴ $∠ B + ∠ D = 180 °$ （           ）

查看试题解析
20. 如图，将三角形ABC先向右平移4个单位长度，再向上平移1个单位长度后得到三角形 $A_{1} B_{1} C_{1}$ ．

(1)、画出平移后的三角形 $A_{1} B_{1} C_{1}$ ；

(2)、写出点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标．

查看试题解析
21. 如图， $A B ∥ C D$ ，直线 $E F$ 分别交 $A B$ 、 $C D$ 于点E，F， $E G$ 平分 $∠ B E F$ ， $∠ 1 = 70 °$ ．求 $∠ 2$ 和 $∠ 3$ 的度数．

查看试题解析
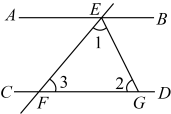22. 已知关于x，y的方程 ${\begin{array}{l} 2 x - y = m \\ 3 x + 2 y = m + 7 \end{array}$ ．

(1)、若 $m = 0$ ，求此时方程组的解；

(2)、若该方程组的解x，y满足点 $A (x ， y)$ ，已知点A为第二象限的点，且该点到x轴的距离为3，到y轴的距离为2，求m的值．

查看试题解析
23. 已知m的算术平方根是3，n的平方根是 $a + 4$ 与 $2 a - 16$ ．

(1)、求m和n的值：

(2)、求 $\sqrt[3]{7 m - n}$ ．

查看试题解析
24. 已知 $A B ∥ C D$ ， $E F$ 分别与 $A B ， C D$ 交于 $E ， F$ ，点 $M$ 是 $E F$ 上的定点，点 $N$ 是直线 $C D$ 上一动点（点 $N$ 不与点 $F$ 重合），

(1)、如图1，若 $∠ A E F = 120 °$ ， $∠ F M N = 50 °$ ，求 $∠ F N M$ 的度数．

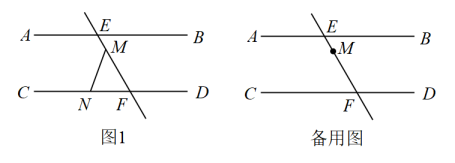(2)、点 $N$ 在运动的过程中，探究 $∠ A E F$ ， $∠ F M N$ 和 $∠ F N M$ 的数量关系，并说明理由．

查看试题解析
25. 如图1，在平面直角坐标系中，已知点 $A (0 ， 2)$ ， $B (4 ， 0)$ ， $C (a ， b)$ ，点 $C$ 在第一象限， $A C$ 平行于 $x$ 轴，且 $A C = 2$ ．点 $P$ 从点 $A$ 出发，以每秒1个单位长度沿 $y$ 轴向下匀速运动；点 $Q$ 从点 $O$ 同时出发，以每秒1个单位长度的速度沿 $x$ 轴向右匀速运动，当点 $Q$ 到达点 $B$ 时停止运动，点 $P$ 也随之停止运动．设运动时间为 $t (t > 0)$ 秒．问：

(1)、 $a =$ ， $b =$ ．

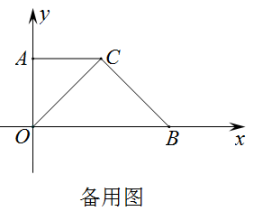(2)、当 $t = 3$ 时，求三角形 $C O P$ 的面积．

(3)、是否存在这样的 $t$ ，使三角形 $B C Q$ 的面积是三角形 $C O P$ 的面积的3倍，若存在，请求出 $t$ 的值；若不存在，请说明理由．

查看试题解析