广东省佛山市顺德区乐从镇2022-2023学年七年级下学期期中数学试卷

试卷更新日期：2023-05-09 类型：期中考试

进入出卷网下载

一、单选题

1. $K N 95$ 型口罩能过滤空气中95%的粒径约为 $0.00000025 m$ 的非油性颗粒，用科学记数法表示0.00000025是（）

A、 $25 \times 1 0^{- 8}$ B、 $0.25 \times 1 0^{- 6}$ C、 $2.5 \times 1 0^{- 6}$ D、 $2.5 \times 1 0^{- 7}$

查看试题解析
2. 已知 $∠ α = 50 °$ ，则它的补角为（）

A、 $40 °$ B、 $60 °$ C、 $130 °$ D、 $140 °$

查看试题解析
3. 下列计算正确的是（）

A、 ${(a^{5})}^{2} = a^{10}$ B、 $a^{9} \div a^{3} = a^{3}$ C、 $b^{3} \cdot b^{3} = 2 b^{3}$ D、 ${(a b)}^{2} = a b^{2}$

查看试题解析
4. 如图，直线 $A B ， C D$ 相交于点O， $O E ⊥ C D$ 于点O，若 $∠ B O E = 40 °$ ，则 $∠ A O C$ 等于（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
5. 用一根10cm长的铁丝围成的长方形，现给出四个量：①长方形的长；②长方形的宽；③长方形的周长；④长方形的面积．其中是变量的有（）

A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析
6. 如图，若 $A B ∥ C D$ ，那么（）．

A、 $∠ 1 = ∠ 3$ B、 $∠ 2 = ∠ 4$ C、 $∠ B + ∠ D = 180 °$ D、 $∠ B = ∠ 3$

查看试题解析
7. 若 $a^{m} = 2$ ， $a^{n} = 3$ ，则 $a^{m + n} =$ （）

A、5 B、6 C、9 D、8

查看试题解析
8. 某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据（如下表）：
温度/ $℃$
-20
-10
0
10
20
30
声速/ $(m / s)$
318
324
330
336
342
348
下列说法错误的是（）

A、在这个变化中，自变量是温度，因变量是声速 B、温度越高，声速越快 C、当空气温度为 $20 ℃$ 时，声速为 $342 m / s$ D、当温度每升高 $10 ℃$ ，声速增加 $8 m / s$

查看试题解析

二、填空题

9. 计算： $2^{- 1}$ =。

查看试题解析
10. 任意给一个非零数 $x$ ，按下列程序写出输出结果：（写出 $y$ 与 $x$ 的关系式）．

查看试题解析
11. 如图，直线 $a$ 、 $b$ 被直线 $c$ 所截，若要使 $a ∥ b$ 则需满足的一个条件是．

查看试题解析
12. 若x²+mx+9是一个完全平方式，则m的值是．

查看试题解析
13. 如图是某灯具的镜面反射示意图，从光源点 $P$ 处发出的光线 $P A$ ， $P B$ 经弯曲的镜面反射后射出，且满足反射光线 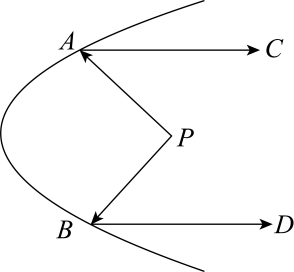$A C ∥ B D$ ，若 $∠ P A C = 40 °$ ， $P A ⊥ P B$ 于点 $P$ ，则 $∠ P B D$ 的度数为．

查看试题解析

三、解答题

14. 计算： ${(3.14 - π)}^{0} + 3^{4} \div 3^{2}$

查看试题解析
15. 先化简，再求值： $[(x + y) (x - y) + {(x - y)}^{2}] \div 2 x$ ，其中 $x = 2$ ， $y = 1$

查看试题解析
16. 如图，已知AB∥CD，∠1＝∠2，求证：AE∥DF．

查看试题解析
17. 如图，阴影部分是一个“ $T$ ”型．

(1)、用含 $x$ ， $y$ 的代数式表示“ $T$ ”型图形的面积并化简；

(2)、若 $x = 5$ 米， $y = 15$ 米，“ $T$ ”型区域铺上价格为每平方米20元的草坪，请计算草坪的造价．

查看试题解析
18. 如图，在 $R t △ A B C$ 中， $∠ A = 90 °$ ，点 $D$ 是线段 $B C$ 上一点．

(1)、尺规作图：在 $△ A B C$ 内作 $∠ C D E = ∠ B$ ，与边 $A C$ 交于点 $E$ （保留作图痕迹，不用写作法）；

(2)、在（1）的条件下，当 $∠ C = 30 °$ 时，求 $∠ C D E$ 的度数．

查看试题解析
19. 为了解某种车的耗油量，我们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来，制成如表：
汽车行驶时间 $t (h)$
0
1
2
3
油箱剩余油量 $Q (L)$
100
94
88
82

(1)、上表反映两个变量中，是自变量；是因变量；

(2)、根据上表的数据，用 $t$ 表示 $Q$ ，表达式为：；

(3)、汽车行驶 $5 h$ 后，油箱中的剩余油量是多少？

(4)、贮满 $100 L$ 汽油的汽车，理论上最多能行驶几小时？

查看试题解析
20. 已知 $A = {(x + y)}^{2} - {(x - y)}^{2}$ ， $B = (2 x^{2} y + 5 x y^{2}) \div x y - 4 x y$ ．

(1)、求 $A$ 和 $B$ ；

(2)、若变量 $x$ ， $y$ 满足 $A + B = 3$ ，求 $y$ 与 $x$ 的关系式；

(3)、在（2）的条件下，求 $4^{x} \cdot 3 2^{y}$ 的值．

查看试题解析
21. 通过构造一个图形，利用两种方法计算该图形的面积，从而得到一个等式，这种方法习惯称为“算两次”，在数学学习中有着广泛的应用．公元三世纪，三国时代的赵爽创制了“勾股圆方图”，验证了著名的勾股定理．

(1)、如图1，边长为 $a$ 的大正方形 $A B C D$ 中有一个边长为 $b$ 的小正方形 $A E F G$ ．请你用两种不同方法求阴影部分的面积；

(2)、如图2，现有若干张 $A$ 型、 $B$ 型、 $C$ 型三种不同形状的纸片，请你利用纸片拼出一个几何图形直观地解释 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ；

(3)、在（1）的条件下，若 $a = 4 c m$ ， $b = 2 c m$ ，一动点 $M$ 以每秒 $1 c m$ 的速度从点 $E$ 出发，沿着 $E \to B \to C \to D \to G$ 方向运动．
①当点 $M$ 在 $E \to B$ 上运动时，请表示出 $△ E F M$ 的面积 $y$ 与 $t$ 的关系式： ▲ ；
②是否存在 $t$ 使得 $△ E F M$ 的面积为 $1 c m^{2}$ ，若存在，求出 $t$ 的值；若不存在，请说明理由．

查看试题解析
22. 将一副三角板中的两个直角顶点 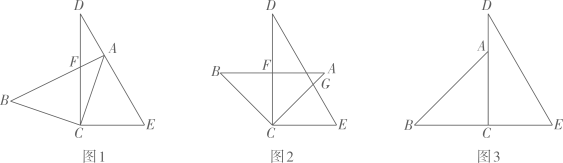$C$ 叠放在一起，其中 $∠ A = ∠ B = 45 °$ ， $∠ D = 30 °$ ， $∠ E = 60 °$

(1)、操作发现：如图1，当点 $A$ 落在线段 $D E$ 上时，写出图中相等的角（写出三对即可）；

(2)、问题解决：如图2，若线段 $A C$ 与 $D E$ 交于点 $G$ ．
①若 $∠ B C E = 3 ∠ A C D$ 时，求 $∠ B C D$ 的度数；
②当 $∠ B C D$ 为何值时，使线段 $C G$ 最短；

(3)、深化拓展：如图3，将三角板 $A B C$ 绕点 $C$ 顺时针转动，直到边 $B C$ 与 $C E$ 重合即停止，转动的过程中当两块三角板恰有两边平行时，请直接写出 $∠ A C D$ 的度数．

查看试题解析

温度/ $℃$	-20	-10	0	10	20	30
声速/ $(m / s)$	318	324	330	336	342	348

汽车行驶时间 $t (h)$	0	1	2	3
油箱剩余油量 $Q (L)$	100	94	88	82