广东省佛山市南海区狮山镇2022-2023学年七年级下学期期中数学试卷
试卷更新日期:2023-05-09 类型:期中考试
一、单选题
-
1. 世界上最小的动物是一种代号为的原生单细胞动物,最大直径长0.3微米,即0.000003米,只有在显微镜下才能看到.其中数字0.000003用科学记数法表示为( )A、 B、 C、 D、2. 如图, , , 则的度数是( )
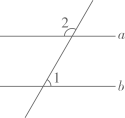 A、 B、 C、 D、3. 如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能符合题意解释这一现象的数学知识是( )
A、 B、 C、 D、3. 如图,某同学在体育课上跳远后留下的脚印,在图中画出了他的跳远距离,能符合题意解释这一现象的数学知识是( ) A、两点之间,线段最短 B、垂线段最短 C、两点确定一条直线 D、经过一点有且只有一条直线与已知直线垂直4. 如图,在 中, 于点 ,点 到直线 的距离是( )
A、两点之间,线段最短 B、垂线段最短 C、两点确定一条直线 D、经过一点有且只有一条直线与已知直线垂直4. 如图,在 中, 于点 ,点 到直线 的距离是( )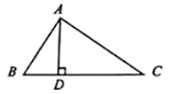 A、线段 的长 B、线段 的长 C、线段 的长 D、线段 的长5. (x+5)(x-3)等于( )A、x2 -15 B、x2 + 15 C、x2 + 2x -15 D、x2 - 2x - 156. 下列运算中正确的是( )A、 B、 C、 D、7. 某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):
A、线段 的长 B、线段 的长 C、线段 的长 D、线段 的长5. (x+5)(x-3)等于( )A、x2 -15 B、x2 + 15 C、x2 + 2x -15 D、x2 - 2x - 156. 下列运算中正确的是( )A、 B、 C、 D、7. 某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):温度(℃)
-20
-10
0
10
20
30
声速()
318
324
330
336
342
348
下列说法中错误的是( )
A、当空气温度为时,5s内声音可以传播 B、温度每升高 , 声速增加 C、在这个变化过程中,自变量是温度,因变量是声速 D、温度越高,声速越快8. 如图 ,将边长为 的大正方形剪去一个边长为 的小正方形(阴影部分),并将剩余部分沿虚线剪开,得到两个长方形,再将这两个长方形拼成图 所示长方形.这两个图能解释下列哪个等式( ) A、 B、 C、 D、9. 如图,不能说明AB//CD的有( )
A、 B、 C、 D、9. 如图,不能说明AB//CD的有( )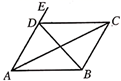
①∠DAC=∠BCA;②∠BAD=∠CDE;③∠DAB+∠ABC=180°;④∠DAB=∠DCB
A、1个 B、2个 C、3个 D、4个10. 观察等式: ; ; 已知按一定规律排列的一组数: 、 、 、 、 、 .若 ,用含 的式子表示这组数的和是( )A、 B、 C、 D、二、填空题
-
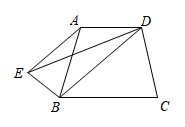
11. 计算 的结果等于12. 已知一个角是 , 则这个角的余角的度数是 .13. 计算: .14. .15. 如图, , 平分 , 且.若 , 则°.
三、解答题
-
16. 计算: .17. 动手操作.已知 , , 求作一个角 , 使它等于与的和.(要求:尺规作图,不在原图上作图,不写作法,保留作图痕迹)
 18. 如图,已知 , , 求 .
18. 如图,已知 , , 求 . 19. 先化简,再求值: , 其中 ,20. 如图,直线AB,CD相交于点O,OE平分∠BOC,∠COF=90°.
19. 先化简,再求值: , 其中 ,20. 如图,直线AB,CD相交于点O,OE平分∠BOC,∠COF=90°. (1)、若∠BOE=65°,求∠AOF的度数;(2)、若∠BOD:∠BOE=1:2,求∠AOF的度数21. 如图所示,梯形的上底长是 , 下底长是 . 当梯形的高由大变小时,梯形的面积也随之发生变化.设梯形的高为 , 面积为 .
(1)、若∠BOE=65°,求∠AOF的度数;(2)、若∠BOD:∠BOE=1:2,求∠AOF的度数21. 如图所示,梯形的上底长是 , 下底长是 . 当梯形的高由大变小时,梯形的面积也随之发生变化.设梯形的高为 , 面积为 . (1)、求梯形的面积与高之间的关系式;(2)、当梯形的高h由变化到时,梯形的面积S如何变化?22. 现有长与宽分别为、的小长方形若干个,用两个这样的小长方形拼成如图1的图形,用四个相同的小长方形拼成图2的图形,请认真观察图形,解答下列问题:
(1)、求梯形的面积与高之间的关系式;(2)、当梯形的高h由变化到时,梯形的面积S如何变化?22. 现有长与宽分别为、的小长方形若干个,用两个这样的小长方形拼成如图1的图形,用四个相同的小长方形拼成图2的图形,请认真观察图形,解答下列问题:
 (1)、根据图中条件,请写出图1和图2所验证的关于、的关系式:(用含、的代数式表示出来);
(1)、根据图中条件,请写出图1和图2所验证的关于、的关系式:(用含、的代数式表示出来);图1表示:;
图2表示:;
(2)、根据上面的解题思路与方法,解决下列问题:①若 , , 求的值;
②请直接写出下列问题故答案为:
若 , , 则 ▲ ;
若 , 则 ▲ .
(3)、如图,长方形中, , , , 长方形的面积是200,四边形和都是正方形,四边形是长方形.延长至 , 使 , 延长至 , 使 , 过点、作、的垂线,两垂线相交于点 , 求四边形的面积.(结果必须是一个具体的数值)23. 几何模型在解题中有着重要作用,例如美味的“猪蹄模型”.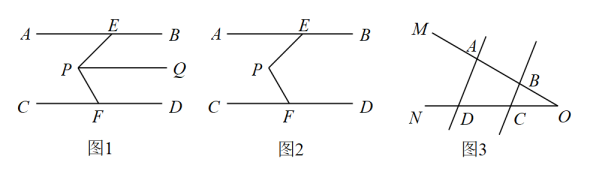 (1)、导入:如图1,已知 , 如果 , , 则;(2)、发现:如图2,直线 , 请判断与 , 之间的数量关系,并说明理由;(3)、运用:如图3,已知 , P在射线上运动(点P与点A、B、O三点不重合), , , 请用含、的代数式表示 , 并说明理由.
(1)、导入:如图1,已知 , 如果 , , 则;(2)、发现:如图2,直线 , 请判断与 , 之间的数量关系,并说明理由;(3)、运用:如图3,已知 , P在射线上运动(点P与点A、B、O三点不重合), , , 请用含、的代数式表示 , 并说明理由.