安徽省安庆市怀宁县2022-2023学年七年级下学期期中数学试卷
试卷更新日期:2023-05-09 类型:期中考试
一、单选题
-
1. 在 , , , , , (两个1之间依次增加一个0)这几个数中无理数有( )A、2个 B、3个 C、4个 D、5个2. 某种细菌的直径为 , 该数据0.0000132用科学记数法表示为( )A、 B、 C、 D、3. 若 , 其中是正整数,则是( )A、1 B、1和2 C、2 D、2和34. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、5. 在数轴上表示不等式组的解集正确的是( )A、
 B、
B、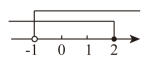 C、
C、 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7. 已知 , , 则的值为( )A、 B、 C、 D、-58. 若 , 则的值为( )A、-6 B、-8 C、 D、9. 若 ,则n为( )A、2022 B、2023 C、2024 D、202510. 关于x的一元一次不等式组有解,则a的取值范围是( )A、 B、 C、 D、
6. 下列运算正确的是( )A、 B、 C、 D、7. 已知 , , 则的值为( )A、 B、 C、 D、-58. 若 , 则的值为( )A、-6 B、-8 C、 D、9. 若 ,则n为( )A、2022 B、2023 C、2024 D、202510. 关于x的一元一次不等式组有解,则a的取值范围是( )A、 B、 C、 D、二、填空题
-
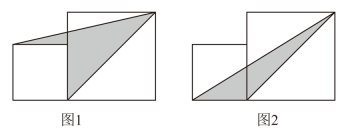
11. 的平方根是 .12. “的3倍与2的差不小于9”列出的不等式是 .13. 因式分解: .14. 将大小不同的两个正方形按图1、图2的方式摆放.若图1中阴影部分的面积是36,图2中阴影部分的面积是27,则大正方形的边长是 .
三、解答题
-
15. 计算:16. 计算:17. 解不等式组: , 并写出此不等式组的整数解.18. 已知的平方根为 , 的立方根为(1)、求 , 的值;(2)、求的值.19. 已知关于x、y的二元一次方程组 的解满足 . 求y的取值范围.20. 从边长为的正方形减掉一个边长为的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
 (1)、上述过程所揭示的乘法公式是 .(2)、若 , , 求的值.(3)、计算: .21. “绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买、两种型号的垃圾处理设备,已知2台型设备和3台型设备日处理能力一共为72吨;3台型设备和1台型设备日处理能力一共为52吨.(1)、求1台型设备、1台型设备日处理能力各为多少吨?(2)、根据实际情况,需购买、两种型号的垃圾处理设备共10台.要求型设备不多于型设备的3倍,且购回的设备日处理能力不低于144吨.请你利用不等式的知识为该景区设计购买、设备的方案.22. 材料阅读:若一个整数能表示成( , 是整数)的形式,则称这个数为“完美数”.
(1)、上述过程所揭示的乘法公式是 .(2)、若 , , 求的值.(3)、计算: .21. “绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买、两种型号的垃圾处理设备,已知2台型设备和3台型设备日处理能力一共为72吨;3台型设备和1台型设备日处理能力一共为52吨.(1)、求1台型设备、1台型设备日处理能力各为多少吨?(2)、根据实际情况,需购买、两种型号的垃圾处理设备共10台.要求型设备不多于型设备的3倍,且购回的设备日处理能力不低于144吨.请你利用不等式的知识为该景区设计购买、设备的方案.22. 材料阅读:若一个整数能表示成( , 是整数)的形式,则称这个数为“完美数”.例如:因为 , 所以是“完美数”;再如:因为( , 是整数),所以是“完美数”.
根据上面的材料,解决下列问题:
(1)、请直接写出一个小于10的“完美数”,这个“完美数”是 .(2)、试判断( , 是整数)是否为“完美数”,并说明理由.(3)、已知M=( , 是整数,为常数),要使为“完美数”,试求出符合条件的值,并说明理由.