山东省青岛市莱西市2022-2023学年八年级下学期期中数学试题
试卷更新日期:2023-05-09 类型:期中考试
一、单选题
-
1. 下列计算正确的是( )A、 =±3 B、 C、 =-3 D、2. 下列方程中,关于x的一元二次方程是( )A、 B、 C、 =0 D、3. 要使二次根式有意义,则x的值可以为 ( )A、-2 B、4 C、2 D、04. 方程的根是( )A、1 B、0 C、0或1 D、0或-15. 用配方法解方程时,下列配方错误的是( ).A、 化为 B、 化为 C、 化为 D、 化为6. 观察下列表格,估计一元二次方程的正数解在( )
-1
0
1
2
3
4
-7
-5
-1
5
13
23
A、-1和0之间 B、0和1之间 C、1和2之间 D、2和3之间7. 下列各组二次根式中,化简后属于同类二次根式的一组是( )A、和 B、和 C、和 D、和8. 已知x1= + ,x2= - ,则x₁²+x₂²等于( )A、8 B、9 C、10 D、119. 为响应“足球进校园”的号召,某校组织足球比赛,赛制为单循环形式(每两个队之间都要比赛一场),计划安排28场比赛,则参赛的足球队个数为( )A、6 B、7 C、8 D、910. 如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )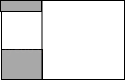 A、 B、2 C、 D、6
A、 B、2 C、 D、6二、填空题
-
11. 计算 .12. 若最简二次根式与是同类二次根式,则的值为 .13. 若关于x的一元二次方程没有实数根,则a的取值范围为 .14. 观察下列等式:
①3﹣2 =( ﹣1)2 , ②5﹣2 =( ﹣ )2 , ③7﹣2 =( ﹣ )2 ,
…
请你根据以上规律,写出第6个等式 .
15. 若等腰三角形的一边长是4,另两边的长是关于 的方程 的两个根,则 的值为 .16. 如图,要设计一幅宽20 , 长30的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为 , 如果要使所有彩条所占面积为原矩形图案面积的三分之一,则横彩条的宽度是 , 竖彩条的宽度是 .
三、解答题
-
17. 计算:(1)、;(2)、;(3)、;(4)、 .18. 解方程:(1)、;(2)、(用配方法).19. 小明在学习中发现了一个“有趣”的现象:
②
③
④
(1)、上面的推导过程中,从第 步开始出现错误(填序号);(2)、写出该步的正确结果.20. 关于的一元二次方程有两个实数根.(1)、求的取值范围:(2)、若为最大负整数,求此时方程的根.21. 已知 , , 试求代数式的值.22. 如图,一矩形花坛一边靠墙,长4m,宽3m,为便于游客赏花,另外三边铺设宽度相等的甬路,若甬路面积恰为花坛面积的 , 求甬路的宽度. 23. 如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头:小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航,一般补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰.
23. 如图,某海军基地位于A处,在其正南方向200海里处有一重要目标B,在B的正东方向200海里处有一重要目标C,小岛D位于AC的中点,岛上有一补给码头:小岛F位于BC上且恰好处于小岛D的正南方向,一艘军舰从A出发,经B到C匀速巡航,一般补给船同时从D出发,沿南偏西方向匀速直线航行,欲将一批物品送达军舰. (1)、小岛D和小岛F相距多少海里?(2)、已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)24. 一些含根号的式子可以写成另一个式子的平方,如3+2=(1+)2 . 设a+b(其中a、b、m、n均为正整数),则有a+b=m2+2n2+2mn , ∴a=m2+2n2 , b=2mn.这样可以把部分a+b的式子化为平方式的方法.请你仿照上述的方法探索并解决下列问题:(1)、当a、b、m、n均为正整数时,若a+b=(m+n)2 , 用含m、n的式子分别表示a、b,得:a= , b= .(2)、利用所探索的结论,找一组正整数a、b、m、n填空:+=(+)2;(3)、化简
(1)、小岛D和小岛F相距多少海里?(2)、已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了多少海里?(结果精确到0.1海里)24. 一些含根号的式子可以写成另一个式子的平方,如3+2=(1+)2 . 设a+b(其中a、b、m、n均为正整数),则有a+b=m2+2n2+2mn , ∴a=m2+2n2 , b=2mn.这样可以把部分a+b的式子化为平方式的方法.请你仿照上述的方法探索并解决下列问题:(1)、当a、b、m、n均为正整数时,若a+b=(m+n)2 , 用含m、n的式子分别表示a、b,得:a= , b= .(2)、利用所探索的结论,找一组正整数a、b、m、n填空:+=(+)2;(3)、化简