江西省新余市2022-2023学年八年级下学期期中数学试卷

试卷更新日期：2023-05-09 类型：期中考试

进入出卷网下载

一、单选题

1. 下列运算或变形正确的是（）

A、 $\sqrt{2} \times \sqrt{3} = 2 \sqrt{3}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $x \sqrt{- \frac{1}{x}} = - \sqrt{x}$ D、 $x \sqrt{- \frac{1}{x}} = - \sqrt{- x}$

查看试题解析
2. 下列图形：①线段；②等腰三角形；③平行四边形；④矩形；⑤菱形；⑥正五边形．是轴对称图形的有（）个

A、3 B、4 C、5 D、6

查看试题解析
3. 如图，矩形 $A B C D$ 中， $A B = 3 ， A D = 1 ， A B$ 在数轴上，若以点A为圆心，对角线 $A C$ 的长为半径作到交数轴的正半轴于M，则点M，在数轴上表示的数为（）

A、2 B、 $\sqrt{5} - 1$ C、 $\sqrt{10} - 1$ D、 $\sqrt{5}$

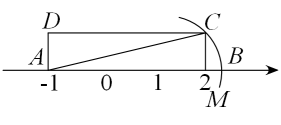查看试题解析
4.
如图，平行四边形ABCD的周长为16cm，AC，BD相交于点O，EO⊥BD交AD于点E，则△ABE的周长为（　　）

A、4cm B、6cm C、8cm D、10cm

查看试题解析
5. 对于实数 $a$ 和 $b$ ，定义一种新运算“ $\otimes$ ”为： $a \otimes b = \frac{1}{1 - b^{2}}$ ，这里等式右边是实数运算．例如： $5 \otimes 3 = \frac{1}{1 - 3^{2}} = - \frac{1}{8}$ ．则方程 $x \otimes 2 = \frac{2}{x - 4} - 1$ 的解是（）

A、 $x = 4$ B、 $x = 5$ C、 $x = 6$ D、 $x = 7$

查看试题解析
6. 若实数 $a, b, c$ 满足条件 $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = \frac{1}{a + b + c}$ ，则 $a, b, c$ 中（）

A、必有两个数相等 B、必有两个数互为相反的数 C、必有两个数互为倒数 D、每两个数都不等

查看试题解析

二、填空题

7. 当m＝时，二次根式 $\sqrt{m - 2}$ 取到最小值．

查看试题解析
8. 已知点 $A (- 1 ， a + 1)$ ， $B (b ， - 3)$ 是关于x轴对称的点， $a - b =$ ．

查看试题解析
9. 若 $2 < m < 8$ ，化简： $\sqrt{{(2 - m)}^{2}} - \sqrt{{(m - 8)}^{2}} =$ ．

查看试题解析
10. 如图，在四边形 $A B C D$ 中， $A B = A D$ ， $∠ A = ∠ C = 90 °$ ，若 $B C + C D = 10 cm$ ，则四边形 $A B C D$ 的面积为 ${cm}^{2}$ .

查看试题解析
11. 如图，在 $R t △ A B C$ 中， $∠ B A C = 90 °$ ，分别以 $A B 、 B C 、 A C$ 为边向上作正方形 $A G F B$ 、正方形 $B C D E$ 、正方形 $A C M N$ ，点 $E$ 在 $F G$ 上，若 $A C = 2 ， B C = \sqrt{13}$ ，则图中阴影的面积为．

查看试题解析
12. 如图，在△ABC中，∠ACB=90°，AC=8，BC=6，D是线段AB的中点，P为直线BC上的一动点，连结DP.过点D作ED⊥DP，交直线AC于点E，连结EP.若CP=3，则AE的长为.

查看试题解析

三、解答题

13.

(1)、计算： $\sqrt[3]{0.008} - \sqrt{0.25} + \sqrt{3} (\sqrt{3} + \frac{1}{\sqrt{3}}) + \sqrt{4}$ ；

(2)、已知 $x^{2} - 3 x - 2 = 0$ ，求代数式 $(x + 1) (x - 1) - {(x + 3)}^{2} + 2 x^{2}$ 的值．

查看试题解析
14. 春节期间，乐乐帮妈妈挂灯笼时，发现，如图长2.5米的梯子 $A B$ 斜靠在一竖直的墙 $A C$ 上，这时 $B C$ 为1.5米，当梯子的底端B向右移动0.5米到D处时，你能帮乐乐算算梯子顶端A下滑多少米吗？（E处）．

查看试题解析
15. 如图，在▱ABCD中，E是BC的中点，AE＝9，BD＝12，AD＝10.

(1)、求证：AE⊥BD；

(2)、求▱ABCD的面积．

查看试题解析
16.

(1)、如下图，矩形ABCD的顶点A在射线OM上，顶点B、C在射线ON上，且OA=OC，只用无刻度的直尺作∠MON的角平分线OP；

(2)、如下图，G为菱形ABCD中CD边的中点，只用无刻度的直尺在对角线AC上求作点P，使 $P G = \frac{1}{2} C D$ ．

查看试题解析
17. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”．

(1)、若 $B C = 3$ ， $A C = 6$ 时，求阴影部分的面积；

(2)、若 $B C \cdot A C = 12$ ，则图中阴影部分的面积为．

查看试题解析
18. 春运期间，某客运站旅客流量不断增大，旅客往往需要很长时间排队等候购票．经调查发现，每天开始售票时，约有400人排队购票．同时又有新的旅客不断进入售票厅排队等候购票，购票时售票厅每分钟新增4人，每分钟每个窗口出售票数 $3$ 张．（规定每人只限购一张）

(1)、若开放两个售票窗口，问开始售票后多少分钟售票厅内有320人？

(2)、若在开始售票20分钟后，来购票的旅客不用排队等待，至少需要开放几个窗口？

查看试题解析
19. 某校为了了解学生的课外阅读情况，从全校随机抽取了部分学生调查了他们的平均每周的课外阅读时间t（单位：小时）．把调查结果分为四档A档： $t \leq 8$ ；B档8≤t≤9；C档 $9 \leq t \leq 10$ ；D档： $t \geq 10$ ．根据调查情况，并绘制成两幅统计图（不完整）．根据以上信息解答问题：

(1)、本次调查的A档次的学生人数有 ▲ 人，并将条形图补充完整；

(2)、C档所在扇形统计图中圆心角的度数为度；

(3)、已知全校共1200名学生，请你估计全校B档和A档共有多少人？

查看试题解析
20. 已知有理数 $m$ 、 $n$ 满足等式 $\sqrt{m - 2} + \sqrt{2 - m} = \sqrt[3]{27} - n$ ．

(1)、求 $m^{n} + 2 m n + 5$ 的平方根；

(2)、计算： $\frac{1}{m - 1 + m} + \frac{1}{m - 1 + m + n} + \frac{1}{m - 1 + m + n + n + 1} + \frac{1}{m - 1 + m + n + n + 1 + n + 2} + \cdot \cdot \cdot \cdot \cdot \cdot + \frac{1}{m - 1 + m + n + n + 1 + n + 2 \cdot \cdot \cdot \cdot \cdot \cdot n + 23}$ ．

查看试题解析
21. 我们已经学过完全平方公式 $a^{2} \pm 2 a b + b^{2} = {(a \pm b)}^{2}$ ，知道所有的非负数都可以看作是一个数的平方，如 $2 = {(\sqrt{2})}^{2}$ ， $3 = {(\sqrt{3})}^{2}$ ， $7 = {(\sqrt{7})}^{2}$ ， $0 = 0^{2}$ ，那么，我们可以利用这种思想方法和完全平方公式来计算下面的题：
例：求 $3 - 2 \sqrt{2}$ 的算术平方根．
解： $3 - 2 \sqrt{2} = 2 - 2 \sqrt{2} + 1 = {(\sqrt{2})}^{2} - 2 \sqrt{2} + 1^{2} = {(\sqrt{2} - 1)}^{2}$ ，
∴ $3 - 2 \sqrt{2}$ 的算术平方根是 $\sqrt{2} - 1$ ．
你看明白了吗？请根据上面的方法化简：

(1)、 $\sqrt{3 + 2 \sqrt{2}}$ ；

(2)、 $\sqrt{10 + 8 \sqrt{3 + 2 \sqrt{2}}}$ ；

(3)、试利用下图求 $R t △ A B C$ 中 $A B$ 和 $B C$ 的比值（结果保留根式形式）．

查看试题解析
22. 如图：

(1)、如图1，若点 $A$ ， $B$ 在直线 $l$ 的同侧，在直线上找一点 $P$ ，使 $A P + B P$ 的值最小．作法如下：作点 $B$ 关于直线 $l$ 的对称点 $B^{'}$ ，连接 $A B^{'}$ 与直线 $l$ 的交点就是所求的点 $P$ ．如图2，在等边三角形 $A B C$ 中，点 $E$ 是 $A B$ 边的中点， $A D$ 是高，且 $A D = 2$ ，在 $A D$ 上找一点 $P$ ，使 $B P + P E$ 的值最小．
作法如下：作点 $B$ 关于直线 $A D$ 的对称点，恰好与点 $C$ 重合，连接 $C E$ 交 $A D$ 于一点，则这点就是所求的点 $P$ ，求 $B P + P E$ 的最小值．

(2)、实践运用：如图3，在四边形 $A B C D$ 中，点 $B$ 与点 $D$ 关于直线 $A C$ 对称，对角线 $A C$ 与 $B D$ 相交于点 $O$ ， $A C = 8$ ，点 $P$ 是对角线 $A C$ 上的一个动点， $A B = B C = C D = A D = B D$ ，点 $M$ 是 $A B$ 的中点，求 $P M + P B$ 的最小值；

(3)、拓展延伸：如图4，在四边形 $A B C D$ 的对角线 $A C$ 上找一点 $P$ ，使 $∠ A P B = ∠ A P D$ ．（保留作图痕迹，不必写出作法）

查看试题解析
23. 如图，在平面直角坐标系中，矩形 $A O C D$ 的顶点 $A (0 ， 2)$ ， $C (2 \sqrt{3} ， 0)$ ．

(1)、求点D到直线 $A C$ 的距离；

(2)、如图， $∠ A O C$ 的角平分线交 $A D$ 于点B，交 $C D$ 的延长线于点E，F为 $B E$ 的中点，连接 $C F$ ，求 $∠ A C F$ 的大小；

(3)、如图，M，N分别是边 $C D$ 和对角线 $A C$ 上的动点，且 $A N = C M$ ，则 $O M + O N$ 的最小值＝．（直接写出结果）

查看试题解析