广东省揭阳市揭东区 2022-2023学年八年级下学期期中教学质量监测数学试卷

试卷更新日期：2023-05-09 类型：期中考试

进入出卷网下载

一、单选题

1. 春节期间，贴春联，送祝福一直是我们的优良传统．我国传统文化中的“福禄寿喜”图（如图）由四个图案构成．这四个图案中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知 $x < y$ ，则下列不等式一定成立的是（　　）

A、 $x - 5 > y - 5$ B、 $- 2 x > - 2 y$ C、 $a^{2} x < a^{2} y$ D、 $\frac{x}{3} > \frac{y}{3}$

查看试题解析
3. 下列现象：①地下水位逐年下降，②传送带的移动，③方向盘的转动，④水龙头的转动；其中属于旋转的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
4. 如图，在 $△ A B C$ 中，直线 $D E$ 是线段 $A C$ 的垂直平分线，若 $A E = 3$ ， $△ A B D$ 的周长为13，则 $△ A B C$ 的周长为（）

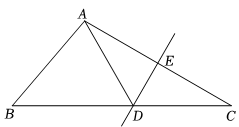A、26 B、16 C、19 D、22

查看试题解析
5. 不等式组 ${\begin{array}{l} 1 - 5 x > 11 \\ 2 x \geq - 10 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在 $△ A B C$ 中， $A B = 10 ， A C = 8 ， O$ 为 $△ A B C$ 角平分线的交点，若 $△ A B O$ 的面积为 $30$ ，则 $△ A C O$ 的面积为（）

A、 $18$ B、 $20$ C、 $22$ D、 $24$

查看试题解析
7. 不等式 $9 - x > x + \frac{2}{3}$ 的正整数解的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 28 °$ 将 $R t △ A B C$ 绕点C按顺时针方向旋转得到 $R t △ D E C$ ，此时点E恰在 $A B$ 边上，则旋转角的大小为（）

A、 $28 °$ B、 $34 °$ C、 $56 °$ D、 $62 °$

查看试题解析
9. 已知方程组 ${\begin{array}{l} 2 x + y = 1 - m \\ x + 2 y = 2 \end{array}$ 的x，y满足x﹣y≥0，则m的取值范围是（）

A、m≤﹣1 B、m≥﹣1 C、m≤1 D、m≥1

查看试题解析
10. 如图，在 $△ A B C$ 中， $A I$ 平分 $∠ B A C$ ， $B I$ 平分 $∠ A B C$ ，点 $O$ 是 $A C$ 、 $B C$ 的垂直平分线的交点，连接 $A O$ 、 $B O$ ，若 $∠ A O B = 140 °$ ，则 $∠ A I B$ 的大小为（）

A、 $90 °$ B、 $105 °$ C、 $125 °$ D、 $145 °$

查看试题解析

二、填空题

11. 若 $(k - 1) x^{| k |} + 3 \geq 0$ 是关于 $x$ 的一元一次不等式，则 $k$ 的值为．

查看试题解析
12. 若点 $A (- 4 ， 2)$ 与点 $B (m ， n)$ 关于原点对称，则 $m - n =$ .

查看试题解析
13. 如图，等边三角形 $A O B$ 绕点 $O$ 旋转到 $△ A^{'} O B^{'}$ 的位置，且 $O A^{'} ⊥ O B$ 则 $△ A O B$ 旋转了度．

查看试题解析
14. 为了打造城市“绿洲”，某市计划在一块如图所示的三角形空地上种植某种草皮，以美化环境，已知这种草皮每平方米售价为 $m$ 元，则购买这种草皮需元．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ C A B = 30 °$ ， $A B = 6$ ，点E、F分别是 $A B$ 、 $B C$ 上的动点，沿 $E F$ 所在直线折叠 $△ E B F$ ，使点B落在 $A C$ 上的点D处，当 $△ A E D$ 是以 $D E$ 为腰的等腰三角形时， $A D$ 的长为．

查看试题解析

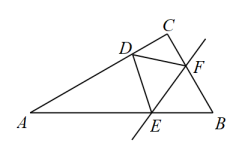
三、解答题

16. 解不等式组 ${\begin{array}{l} 5 x + 1 \geq 3 (x + 1) \\ \frac{1}{2} x < 8 - \frac{3}{2} x \end{array}$ ，并把解集在数轴上表示出来．

查看试题解析
17. 如图， $△ A B C$ 中， $B D$ 平分 $∠ A B C$ ， $B C$ 的中垂线交 $B C$ 于点 $E$ ，交 $B D$ 于点 $F$ ，连接 $C F$ ．若 $∠ A = 60 °$ ， $∠ A B D = 24 °$ ，求 $∠ A C F$ 的度数．

查看试题解析
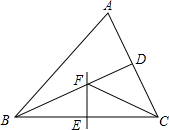18. 已知△ABC在平面直角坐标系中的位置如图所示．

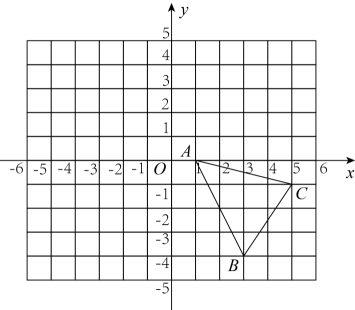(1)、平移△ABC，使点B平移到对应点B′（-3，0），画出△A′B′C′；

(2)、若点P（a，b）是△ABC内部一点，则平移后△A′B′C′内对应点P′的坐标为；

(3)、求△ABC的面积．

查看试题解析
19. 已知关于 $x$ 的方程 $2 x - a = 3$ ，

(1)、若该方程的解满足 $x > 1$ ，求 $a$ 的取值范围；

(2)、若该方程的解是不等式 $3 (x - 2) + 5 < 4 (x - 1)$ 的最小整数解，求 $a$ 的值．

查看试题解析
20. 如图，在 $Δ A B C$ 中， $∠ C = 90 °$ ，点 $P$ 在 $A C$ 上运动，点 $D$ 在 $A B$ 上运动， $P D$ 始终保持与 $P A$ 相等， $B D$ 的垂直平分线交 $B C$ 于点 $E$ ，交 $B D$ 于点 $F$ ，连接 $D E$ ．

(1)、判断 $D E$ 与 $P D$ 的位置关系，并说明理由；

(2)、若 $A C = 3$ ， $B C = 4$ ， $P A = 1$ ，求线段 $D E$ 的长．

查看试题解析
21. 如图， $△ A B C$ 是边长为4cm的等边三角形，边 $A B$ 在射线 $O M$ 上，且 $O A = 6 c m$ ，点D从O点出发，沿 $O M$ 方向以 $1 c m / s$ 的速度运动，运动时间为t．当点D不与点A重合时，将 $△ A C D$ 绕点C逆时针方向旋转 $60 °$ 得到 $△ B C E$ ，连接 $D E$ ．

(1)、求证： $△ C D E$ 是等边三角形．

(2)、当 $△ B C D$ 为直角三角形时，求t的值．

查看试题解析
22. 某电器经营老板计划购进同种型号的空调和电风扇，若购进8台空调和20台电风扇，需要资金17400元，若购进10台空调和30台电风扇，需要资金22500元.

(1)、求空调和电风扇的采购价各是多少元？

(2)、该老板计划购进这两种电器共70台，而可用于购买这两种电器的资金不超过30000元，根据市场行情，销售一台这样的空调可获利200元，销售一台这样的电风扇可获利30元，该老板希望当这两种电器销售完时，所获的利润不少于3500元，试问老板有哪几种进货方案？

(3)、在所有的进货方案中，哪种方案获利最大？最大利润是多少？

查看试题解析
23. 如图1，已知 $∠ D A C = 90 °$ ， $△ A B C$ 是等边三角形，点 $P$ 为射线 $A D$ 上任意一点（点 $P$ 与点 $A$ 不重合），连接 $C P$ ，将线段 $C P$ 绕点 $C$ 顺时针旋转 $60 °$ 得到线段 $C Q$ ，连接 $Q B$ 并延长交直线 $A D$ 于点 $E$ ．

(1)、如图1，猜想 $∠ Q E P =$ $°$ ．

(2)、如图2、3，若当 $∠ D A C$ 是锐角或钝角时，其它条件不变，猜想 $∠ Q E P$ 的度数，选取一种情况加以证明；

(3)、如图3，若 $∠ D A C = 120 °$ ， $∠ A C P = 15 °$ ，且 $A C = 6$ ，求 $B Q$ 的长．

查看试题解析