广东省东莞市常平镇2022-2023学年八年级下学期期中数学试卷
试卷更新日期:2023-05-09 类型:期中考试
一、单选题
-
1. 在“珍爱生命,远离毒品”的禁毒标语中,下列文字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,盖房子时,在窗框没有安装之前,木工师傅常常先在窗框上斜钉一根木条,使其不变形,这种做法的根据是( )
2. 如图,盖房子时,在窗框没有安装之前,木工师傅常常先在窗框上斜钉一根木条,使其不变形,这种做法的根据是( ) A、两点之间线段最短 B、长方形的对称性 C、长方形四个角都是直角 D、三角形的稳定性3. 要使分式有意义,则x的取值范围是( )A、 B、 C、 D、4. 如图,和相交于点,若 , 不能证明的是( )
A、两点之间线段最短 B、长方形的对称性 C、长方形四个角都是直角 D、三角形的稳定性3. 要使分式有意义,则x的取值范围是( )A、 B、 C、 D、4. 如图,和相交于点,若 , 不能证明的是( ) A、 B、 C、 D、5. 下列长度的3根小木棒,能够搭成三角形的是( )A、3 cm 4cm 8cm B、5 cm 6cm 7cm C、4 cm 5cm 10cm D、5cm 7cm 12cm6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,直线 , 的顶点C在直线b上,边与直线b相交于点D.若是等边三角形, , 则( )
A、 B、 C、 D、5. 下列长度的3根小木棒,能够搭成三角形的是( )A、3 cm 4cm 8cm B、5 cm 6cm 7cm C、4 cm 5cm 10cm D、5cm 7cm 12cm6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,直线 , 的顶点C在直线b上,边与直线b相交于点D.若是等边三角形, , 则( ) A、 B、 C、 D、8. 三角形的下列线段中能将三角形的面积分成相等的两部分的是( )A、三角形的中线 B、三角形的角平分线 C、三角形的高 D、以上答案均符合题意9. 设 , , 则 , 的关系是( )A、 B、 C、 D、10. 如图,中, , 是角平分线, , , E、F为垂足,对于结论:①;②;③上任一点到、的距离相等;④上任一点到B、C的距离相等.其中正确的是( )
A、 B、 C、 D、8. 三角形的下列线段中能将三角形的面积分成相等的两部分的是( )A、三角形的中线 B、三角形的角平分线 C、三角形的高 D、以上答案均符合题意9. 设 , , 则 , 的关系是( )A、 B、 C、 D、10. 如图,中, , 是角平分线, , , E、F为垂足,对于结论:①;②;③上任一点到、的距离相等;④上任一点到B、C的距离相等.其中正确的是( ) A、仅①② B、仅③④ C、仅①②③ D、①②③④
A、仅①② B、仅③④ C、仅①②③ D、①②③④二、填空题
-
11. 某种细菌的直径是 , 用科学记数法表示为:.12. 因式分解: .13. 六边形的内角和为 .14. 如图, , 点B,C,D在同一条直线上,且 , , 则的长是 .
 15. 如图,在中, , 是高, , 若 , 则 .
15. 如图,在中, , 是高, , 若 , 则 .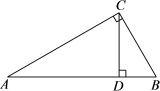 16. 已知 , , 则 .17. 如图,在的边、上取点、 , 连接 , 平分 , 平分 , 若 , 的面积是2,的面积是8.则的长是.
16. 已知 , , 则 .17. 如图,在的边、上取点、 , 连接 , 平分 , 平分 , 若 , 的面积是2,的面积是8.则的长是.
三、解答题
-
18. 计算: .19. 解方程:20. 如图,是上的两点,且 , , . 求证: .
 21. 在中, .
21. 在中, . (1)、尺规作图:求作的垂直平分线 , 分别交 , 于点 , ;(2)、在(1)的条件下,连接 , 若 , 求的度数.22. 先化简: , 然后在-2,-1,2三个数中给a选择一个你喜欢的数代入求值.23. 某公司计划从商店购买同一品牌的毛巾和同一品牌的香皂,已知购买一条毛巾比购买一块香皂多用20元,若用400元购买毛巾,用160元购买香皂,则购买毛巾的条数是购买香皂块数的一半.(1)、购买一条该品牌毛巾、一块该品牌香皂各需要多少元?(2)、经商谈,商店给予该公司购买一条该品牌毛巾赠送一块该品牌香皂的优惠,如果该公司需要香皂的块数是毛巾条数的2倍还多8个,且该公司购买毛巾和香皂的总费用不超过670元,那么该公司最多可购买多少条该品牌毛巾?
(1)、尺规作图:求作的垂直平分线 , 分别交 , 于点 , ;(2)、在(1)的条件下,连接 , 若 , 求的度数.22. 先化简: , 然后在-2,-1,2三个数中给a选择一个你喜欢的数代入求值.23. 某公司计划从商店购买同一品牌的毛巾和同一品牌的香皂,已知购买一条毛巾比购买一块香皂多用20元,若用400元购买毛巾,用160元购买香皂,则购买毛巾的条数是购买香皂块数的一半.(1)、购买一条该品牌毛巾、一块该品牌香皂各需要多少元?(2)、经商谈,商店给予该公司购买一条该品牌毛巾赠送一块该品牌香皂的优惠,如果该公司需要香皂的块数是毛巾条数的2倍还多8个,且该公司购买毛巾和香皂的总费用不超过670元,那么该公司最多可购买多少条该品牌毛巾?

